沪科版八年级数学上册12.1函数试题 一课一练(含答案)
文档属性
| 名称 | 沪科版八年级数学上册12.1函数试题 一课一练(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 94.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-12 16:49:49 | ||
图片预览



文档简介
12.1函数
一、选择题
1.在圆周长的计算公式C=2πr中,变量有( )
A.C,π B.C,r C.C,π,r D.C,2π,r
2.在圆的周长计算公式C=2πR中,对于变量和常量的说法正确的是( )
A.2是常量,C,π,R是变量 B.2,π是常量,C,R是变量
C.2,C,π是常量,R是变量 D.2,π,R是常量,C是变量
3.司机王师傅在加油站加油,如图是所用的加油机上的数据显示牌,则其中的常量是( )
A.金额 B.数量 C.单价 D.金额和数量
4.下列各曲线中不能表示y是x的函数的是( )
A. B.
C. D.
5.已知弹簧的长度y(cm)与所挂物体的质量x(kg)之间有如表关系,则( )
x(kg) 0 1 2 3 4 5
y(cm) 6 6.5 7 7.5 8 8
A.y随x的增大而增大
B.质量每增加1kg,长度增加0.5cm
C.不挂物体时,长度为6cm
D.质量为6kg时,长度为8.5cm
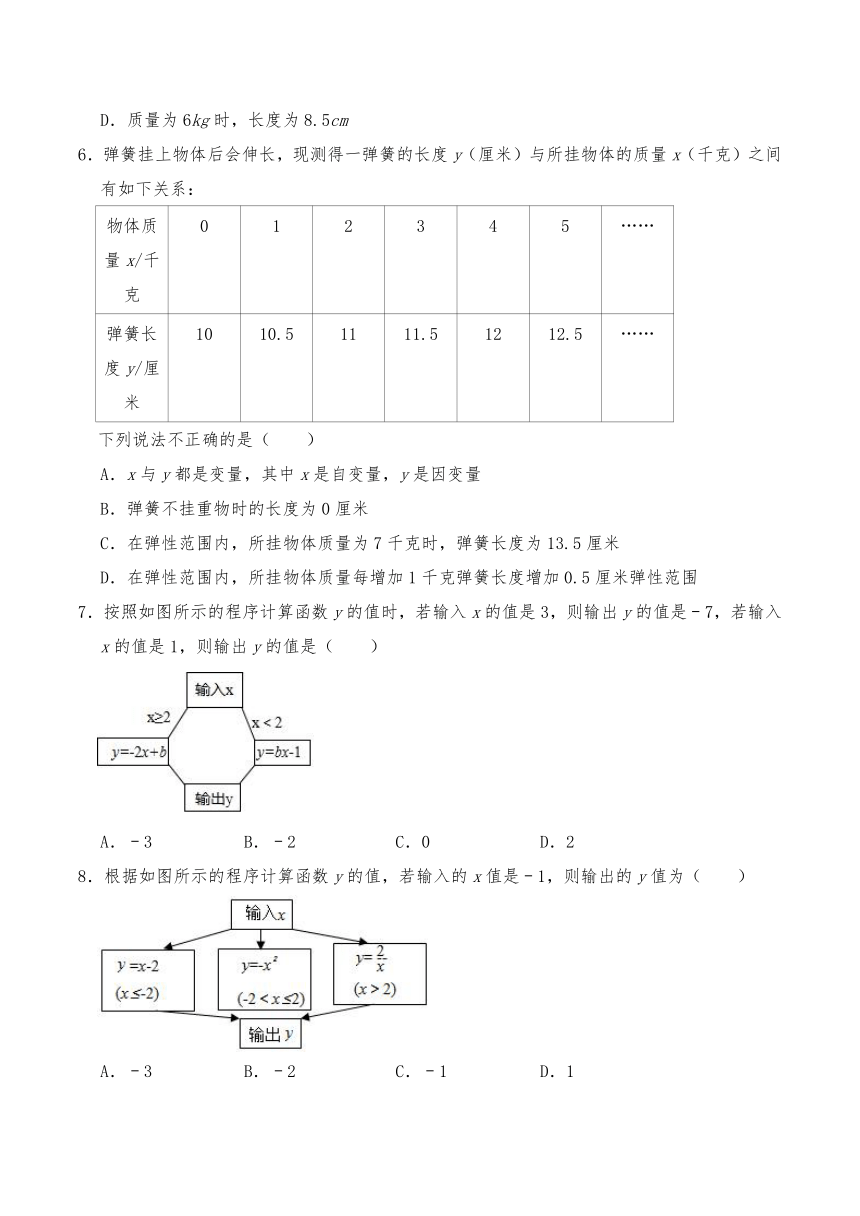
6.弹簧挂上物体后会伸长,现测得一弹簧的长度y(厘米)与所挂物体的质量x(千克)之间有如下关系:
物体质量x/千克 0 1 2 3 4 5 ……
弹簧长度y/厘米 10 10.5 11 11.5 12 12.5 ……
下列说法不正确的是( )
A.x与y都是变量,其中x是自变量,y是因变量
B.弹簧不挂重物时的长度为0厘米
C.在弹性范围内,所挂物体质量为7千克时,弹簧长度为13.5厘米
D.在弹性范围内,所挂物体质量每增加1千克弹簧长度增加0.5厘米弹性范围
7.按照如图所示的程序计算函数y的值时,若输入x的值是3,则输出y的值是﹣7,若输入x的值是1,则输出y的值是( )
A.﹣3 B.﹣2 C.0 D.2
8.根据如图所示的程序计算函数y的值,若输入的x值是﹣1,则输出的y值为( )
A.﹣3 B.﹣2 C.﹣1 D.1
9.某地区用电量与应缴电费之间的关系如下表:则下列叙述错误的是( )
用电量(千瓦 时) 1 2 3 4 …
应缴电费(元) 0.55 1.10 1.65 2.20 …
A.用电量每增加1千瓦 时,电费增加0.55元
B.若用电量为8千瓦 时,则应缴电费4.4元
C.若应缴电费为2.75元,则用电量为6千瓦 时
D.应缴电费随用电量的增加而增加
10.某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如下表):
温度/℃ ﹣20 ﹣10 0 10 20 30
声速/m/s 318 324 330 336 342 348
下列说法错误的是( )
A.在这个变化中,自变量是温度,因变量是声速
B.温度越高,声速越快
C.当空气温度为20℃时,声音5s可以传播1740m
D.当温度每升高10℃,声速增加6m/s
二、填空题
11.函数y的自变量x的取值范围是 .
12.已知f(x)=x2+3x,那么f(﹣2)= .
13.骆驼被称为“沙漠之舟”,它的体温随时间的变化而变化,在这一变量关系中,因变量是 .
14.圆的面积S与半径R之间的关系是S=πR2.请指出公式S=πR2中常量是 .
15.李师傅到单位附近的加油站加油,如图是所用的加油机上的数据显示牌,则其中的常量是 .
16.弹簧挂上物体后会伸长,测得一弹簧的长度y (cm)与所挂的物体的质量x(kg)之间有下面的关系:
x/kg 0 1 2 3 4 5
y/cm 10 10.5 11 11.5 12 12.5
下列说法正确的是 .
①x与y都是变量;
②弹簧不挂重物时的长度为0cm;
③物体质量每增加1kg,弹簧长度增加0.5cm;
④所挂物体质量为7kg时,弹簧长度为13.5cm.
17.某烤鸭店在确定烤鸭的烤制时间时,主要依据的是如表数据:
鸭的质量/千克 0.5 1 1.5 2 2.5 3 3.5
烤制时间/分钟 40 60 80 100 120 140 160
设鸭的质量为x千克,烤制时间为t,估计当x=2.2千克时,t的值为 .
18.某种树木的分枝生长规律如图所示,则预计到第6年时,树木的分枝数为 ,其中自变量是 ,因变量是 .
年份 第一年 第二年 第三年 第四年 第五年
分枝数 1 1 2 3 5
三、解答题
19.指出下列变化过程中,哪个变量随着另一个变量的变化而变化?
(1)一辆汽车以80km/h的速度匀速行驶,行驶的路程s(km)与行驶时间t(h)
(2)圆的半径r和圆面积S满足:S=πr2.
(3)银行的存款利率P与存期t.
20.按如图方式摆放餐桌和椅子.用x来表示餐桌的张数,用y来表示可坐人数.
(1)题中有几个变量?
(2)你能写出两个变量之间的关系吗?
21.科学家认为二氧化碳(CO2)的释放量越来越多是全球变暖的原因之一.下表是1950~1990年全世界所释放的二氧化碳量:
年份 1950 1960 1970 1980 1990
CO2释放量/百万吨 6002 9475 14989 19287 22588
(1)上表反映的是哪两个变量之间的关系?
(2)说一说这两个变量之间的关系.
22.写出下列各问题中的关系式中的常量与变量:
(1)分针旋转一周内,旋转的角度n(度)与旋转所需要的时间t(分)之间的关系式n=6t;
(2)一辆汽车以40千米/时的速度向前匀速直线行驶时,汽车行驶的路程S(千米)与行驶时间t(时)之间的关系式s=40t.
23.婴儿在6个月、1周岁、2周岁时体重分别大约是出生时的2倍、3倍、4倍,6周岁、10周岁时体重分别约是1周岁的2倍、3倍.
(1)上述的那些量在发生变化?自变量和因变量各是什么?
(2)某婴儿在出生时的体重是3.5kg,请把他在发育过程的体重情况填入下表:
年龄 出生时 6个月 1周岁 2周岁 6周岁 10周岁
体重/kg
(3)根据表格中的数据,说一说儿童从出生到10周岁之间体重是怎样随年龄增长而变化的.
24.如图,圆柱的高是3cm,当圆柱的底面半径rcm由小到大变化时,圆柱的体积Vcm3也随之发生了变化.
(1)在这个变化中,自变量是 ,因变量是 ;
(2)写出体积V与半径r的关系式;
(3)当底面半径由1cm到10cm变化时,通过计算说明圆柱的体积增加了多少cm3.
答案
一、选择题
B.B.C.A.C.B.B.C.C.C.
二、填空题
11.x<3.
12.﹣2.
13.体温
14.π.
15.6.48.
16.①③④
17.108.
18.8,年份,分枝数.
三、解答题
19.(1)s=80t,s随着t的变化而变化;
(2)圆的半径r和圆面积S关系式S=πr2,其中S随着r的变化而变化;
(3)银行的存款利率P随着存期t的变化而变化.
20.(1)观察图形:x=1时,y=6,x=2时,y=10;x=3时,y=14;…
可见每增加一张桌子,便增加4个座位,
因此x张餐桌共有6+4(x﹣1)=4x+2个座位.
故可坐人数y=4x+2,
故答案为:有2个变量;
(2)能,由(1)分析可得:函数关系式可以为y=4x+2.
21.(1)上标反映的是CO2释放量与年份之间的关系;
(2)CO2释放量的随着年份的增加而增大.
22.(1)常量:6;变量:n,t.
(2)常量:40;变量:s,t.
23.(1)年龄在逐渐变大,体重在逐渐变重,年龄是自变量,体重是因变量;
(2)
(3)10周岁前的体重随年龄的增长而增大,从刚出生到六个月生长的最快.
24.(1)在这个变化过程中,自变量是r,因变量是V.
故答案为:r,V;
(2)圆柱的体积V与底面半径r的关系式是 V=3πr2.
(3)(π×102﹣π×12)×3=297π(cm3).
所以当底面半径由1cm到10cm变化时,圆柱的体积增加了297πcm3.
一、选择题
1.在圆周长的计算公式C=2πr中,变量有( )
A.C,π B.C,r C.C,π,r D.C,2π,r
2.在圆的周长计算公式C=2πR中,对于变量和常量的说法正确的是( )
A.2是常量,C,π,R是变量 B.2,π是常量,C,R是变量
C.2,C,π是常量,R是变量 D.2,π,R是常量,C是变量
3.司机王师傅在加油站加油,如图是所用的加油机上的数据显示牌,则其中的常量是( )
A.金额 B.数量 C.单价 D.金额和数量
4.下列各曲线中不能表示y是x的函数的是( )
A. B.
C. D.
5.已知弹簧的长度y(cm)与所挂物体的质量x(kg)之间有如表关系,则( )
x(kg) 0 1 2 3 4 5
y(cm) 6 6.5 7 7.5 8 8
A.y随x的增大而增大
B.质量每增加1kg,长度增加0.5cm
C.不挂物体时,长度为6cm
D.质量为6kg时,长度为8.5cm
6.弹簧挂上物体后会伸长,现测得一弹簧的长度y(厘米)与所挂物体的质量x(千克)之间有如下关系:
物体质量x/千克 0 1 2 3 4 5 ……
弹簧长度y/厘米 10 10.5 11 11.5 12 12.5 ……
下列说法不正确的是( )
A.x与y都是变量,其中x是自变量,y是因变量
B.弹簧不挂重物时的长度为0厘米
C.在弹性范围内,所挂物体质量为7千克时,弹簧长度为13.5厘米
D.在弹性范围内,所挂物体质量每增加1千克弹簧长度增加0.5厘米弹性范围
7.按照如图所示的程序计算函数y的值时,若输入x的值是3,则输出y的值是﹣7,若输入x的值是1,则输出y的值是( )
A.﹣3 B.﹣2 C.0 D.2
8.根据如图所示的程序计算函数y的值,若输入的x值是﹣1,则输出的y值为( )
A.﹣3 B.﹣2 C.﹣1 D.1
9.某地区用电量与应缴电费之间的关系如下表:则下列叙述错误的是( )
用电量(千瓦 时) 1 2 3 4 …
应缴电费(元) 0.55 1.10 1.65 2.20 …
A.用电量每增加1千瓦 时,电费增加0.55元
B.若用电量为8千瓦 时,则应缴电费4.4元
C.若应缴电费为2.75元,则用电量为6千瓦 时
D.应缴电费随用电量的增加而增加
10.某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如下表):
温度/℃ ﹣20 ﹣10 0 10 20 30
声速/m/s 318 324 330 336 342 348
下列说法错误的是( )
A.在这个变化中,自变量是温度,因变量是声速
B.温度越高,声速越快
C.当空气温度为20℃时,声音5s可以传播1740m
D.当温度每升高10℃,声速增加6m/s
二、填空题
11.函数y的自变量x的取值范围是 .
12.已知f(x)=x2+3x,那么f(﹣2)= .
13.骆驼被称为“沙漠之舟”,它的体温随时间的变化而变化,在这一变量关系中,因变量是 .
14.圆的面积S与半径R之间的关系是S=πR2.请指出公式S=πR2中常量是 .
15.李师傅到单位附近的加油站加油,如图是所用的加油机上的数据显示牌,则其中的常量是 .
16.弹簧挂上物体后会伸长,测得一弹簧的长度y (cm)与所挂的物体的质量x(kg)之间有下面的关系:
x/kg 0 1 2 3 4 5
y/cm 10 10.5 11 11.5 12 12.5
下列说法正确的是 .
①x与y都是变量;
②弹簧不挂重物时的长度为0cm;
③物体质量每增加1kg,弹簧长度增加0.5cm;
④所挂物体质量为7kg时,弹簧长度为13.5cm.
17.某烤鸭店在确定烤鸭的烤制时间时,主要依据的是如表数据:
鸭的质量/千克 0.5 1 1.5 2 2.5 3 3.5
烤制时间/分钟 40 60 80 100 120 140 160
设鸭的质量为x千克,烤制时间为t,估计当x=2.2千克时,t的值为 .
18.某种树木的分枝生长规律如图所示,则预计到第6年时,树木的分枝数为 ,其中自变量是 ,因变量是 .
年份 第一年 第二年 第三年 第四年 第五年
分枝数 1 1 2 3 5
三、解答题
19.指出下列变化过程中,哪个变量随着另一个变量的变化而变化?
(1)一辆汽车以80km/h的速度匀速行驶,行驶的路程s(km)与行驶时间t(h)
(2)圆的半径r和圆面积S满足:S=πr2.
(3)银行的存款利率P与存期t.
20.按如图方式摆放餐桌和椅子.用x来表示餐桌的张数,用y来表示可坐人数.
(1)题中有几个变量?
(2)你能写出两个变量之间的关系吗?
21.科学家认为二氧化碳(CO2)的释放量越来越多是全球变暖的原因之一.下表是1950~1990年全世界所释放的二氧化碳量:
年份 1950 1960 1970 1980 1990
CO2释放量/百万吨 6002 9475 14989 19287 22588
(1)上表反映的是哪两个变量之间的关系?
(2)说一说这两个变量之间的关系.
22.写出下列各问题中的关系式中的常量与变量:
(1)分针旋转一周内,旋转的角度n(度)与旋转所需要的时间t(分)之间的关系式n=6t;
(2)一辆汽车以40千米/时的速度向前匀速直线行驶时,汽车行驶的路程S(千米)与行驶时间t(时)之间的关系式s=40t.
23.婴儿在6个月、1周岁、2周岁时体重分别大约是出生时的2倍、3倍、4倍,6周岁、10周岁时体重分别约是1周岁的2倍、3倍.
(1)上述的那些量在发生变化?自变量和因变量各是什么?
(2)某婴儿在出生时的体重是3.5kg,请把他在发育过程的体重情况填入下表:
年龄 出生时 6个月 1周岁 2周岁 6周岁 10周岁
体重/kg
(3)根据表格中的数据,说一说儿童从出生到10周岁之间体重是怎样随年龄增长而变化的.
24.如图,圆柱的高是3cm,当圆柱的底面半径rcm由小到大变化时,圆柱的体积Vcm3也随之发生了变化.
(1)在这个变化中,自变量是 ,因变量是 ;
(2)写出体积V与半径r的关系式;
(3)当底面半径由1cm到10cm变化时,通过计算说明圆柱的体积增加了多少cm3.
答案
一、选择题
B.B.C.A.C.B.B.C.C.C.
二、填空题
11.x<3.
12.﹣2.
13.体温
14.π.
15.6.48.
16.①③④
17.108.
18.8,年份,分枝数.
三、解答题
19.(1)s=80t,s随着t的变化而变化;
(2)圆的半径r和圆面积S关系式S=πr2,其中S随着r的变化而变化;
(3)银行的存款利率P随着存期t的变化而变化.
20.(1)观察图形:x=1时,y=6,x=2时,y=10;x=3时,y=14;…
可见每增加一张桌子,便增加4个座位,
因此x张餐桌共有6+4(x﹣1)=4x+2个座位.
故可坐人数y=4x+2,
故答案为:有2个变量;
(2)能,由(1)分析可得:函数关系式可以为y=4x+2.
21.(1)上标反映的是CO2释放量与年份之间的关系;
(2)CO2释放量的随着年份的增加而增大.
22.(1)常量:6;变量:n,t.
(2)常量:40;变量:s,t.
23.(1)年龄在逐渐变大,体重在逐渐变重,年龄是自变量,体重是因变量;
(2)
(3)10周岁前的体重随年龄的增长而增大,从刚出生到六个月生长的最快.
24.(1)在这个变化过程中,自变量是r,因变量是V.
故答案为:r,V;
(2)圆柱的体积V与底面半径r的关系式是 V=3πr2.
(3)(π×102﹣π×12)×3=297π(cm3).
所以当底面半径由1cm到10cm变化时,圆柱的体积增加了297πcm3.
