人教版八年级上册12.2 全等三角形的判定(第3课时)(ASA和AAS)课件(共19张PPT)
文档属性
| 名称 | 人教版八年级上册12.2 全等三角形的判定(第3课时)(ASA和AAS)课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 151.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-12 13:49:40 | ||
图片预览






文档简介
(共19张PPT)
第十二章全等三角形
12.2 全等三角形的判定
第三课时(ASA,AAS)
人教版
八年级上册
学习目标
1.通过动手操作,合作交流、分析、归纳,经历全等三角形的识别方法--“角边角”,“角角边”定理的探索过程,掌握这种识别方法,并会用此定理进行简单的推理;
2.能运用“边角边”,“角角边”定理这个方法证明三角形全等及解决实际问题。
情境
导
入
我们已经知道:三角形全等的判定条件有哪些
“SSS"和“ SAS”。
那除了这两个条件,满足另一些条件的两个三角形是否也可能全等呢
一张教学用的三角形硬纸板不小心被撕坏了(如图所示),你能制作一张与原来同样大小的新教具吗 恢复原来三角形的原貌吗
选取①纸片,
①
②
③
讲
授
新
知
一 探究两角夹边三角形全等
探究3:
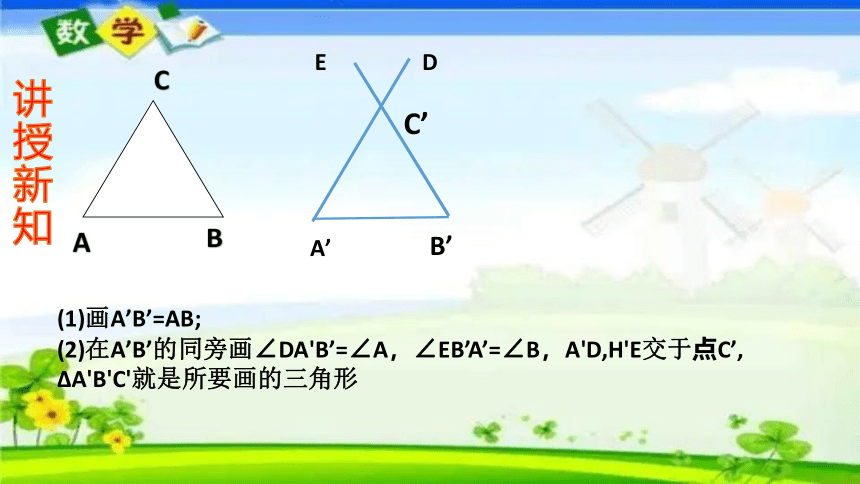
先任意画出一个△ABC,再画出一个△A’B'C',使A'B'=AB,∠B’=∠B, ∠A’=∠A(即两角和它们的夹边分别相等).把画好的ΔA'B’C'剪下来,放到△ABC上,它们全等吗
如何用尺规作图,画出一个△A’B'C'?
(1)画A’B’=AB;
(2)在A’B’的同旁画∠DA'B’=∠A,∠EB’A’=∠B,A'D,H'E交于点C’,
ΔA'B'C'就是所要画的三角形
A
B
C
讲
授
新
知
A’
B’
D
E
C’
这个探究结果反快了什么规律 试着说说你的发现
讲
授
新
知
两角和一边分别相等的两个三角形全等,
两角和它们的夹边分别相等的两个三角形全等
两角和它们的夹边分别相等的两个三角形全等(可以简写成"角边角"或“ASA”)
注意,"边"必须是“两角的夹边".
讲
授
新
知
利用今天“边角边”的知识,我们就可以解决课前问题了,现在你会解释了吗
二 运用“角边角”判定方法,解决简单问题
第一块玻璃,因为它完整的保留了两角及夹边,一个角形两个角的大小和它们的夹边的长度确定了,这个三角形的形状、大小就确定下来了。
例3:如图所示,点D在AB上,点E在AC上,AB=AC, ∠B=∠C.求证:AD=AE.
讲
授
新
知
分析:AD和AE分别在△ADC 和△AEB中,所以要证AD=AE,只需证明△ADC≌ΔAEB 即可.
B
C
D
A
E
例3:如图所示,点D在AB上,点E在AC上,AB=AC, ∠B=∠C.求证:AD=AE.
讲
授
新
知
B
C
D
A
E
证明:在△ADC 和△AEB中,
∠A=∠A,
AC=AB,
∠C=∠B,
∴△ADC≌△AEB(ASA)
∴AD=AE.
讲
授
新
知
如图所示,在△ABC和△DEF中,∠A=∠D,∠B=∠E, BC=EF,△ABC 与△DEF 全等吗 能利用角边角条件证明你的结论吗
三 探究两角一边判定三角形全等
看已知条件,能否用“角边角”条件证明
A
B
C
F
E
D
讲
授
新
知
三 探究两角一边判定三角形全等
证明:在ABC中,∠A+∠B+∠C=180°,
∴∠C=180-∠A-∠B,
A
B
C
F
E
D
同理:在DEF中,∴∠F=180°-∠D-∠E,
∵∠A=∠D,∠B=∠E,
∴∠C=∠F,
讲
授
新
知
三 探究两角一边判定三角形全等
A
B
C
F
E
D
证明:在△ABC 和△DEF中,
∠B=∠E,
BC=EF,
∠C=∠F,
∴△ABC≌△DEF(ASA)
讲
授
新
知
三 探究两角一边判定三角形全等
从上面可以看出,从这些已知条件中能得到两个三角形全等,这又反映了一个什么规律?
两角和其中一条边分别相等的两个三角形全等
在"ASA”中“边必须是"两角的夹边”,而这里,边可以是"其中一个角的对边”,强调 “AAS"中的边是"其中一个角的对边"。
这里的"边”是其中一个角对边那怎样更完整地表述这一规律
两角和其中一个角的对边分别相等的两个三角形全等(可以简写成“角角边”或"AAS ”)
讲
授
新
知
四 探究三角分别相等的三角形不全等
三角对应相等的两个三角形全等吗 想想,怎样来探究这个问题?
用两个同一形状,大小不同的三角板
这一规律我们可以怎样表达
有三个角对应相等的两个三角形不一定全等(没有“角角角”或”AAA”)
讲
授
新
知
四 探究三角分别相等的三角形全等
判定两个三角形全等我们已有了哪些方法
SSS,SAS,ASA,AAS.
通过上面的4种判定方法可以看出.至少具备3个条件,才能判定三角形全等 这三个条件有么要求吗
三个条件中必须有边,可以没有角。
1.已知AB=A’B’,∠A=∠A’,∠B=∠B’,则△ABC≌△A’B’C’的依据是( ).
A. SAS B. SSA C.ASA D.AAS
巩
固
应用
C
2. 在△ABC和△DEF中,AB=DE,∠B=∠E, 要使△ABC 与△DEF 全等,则下列补充的条件中错误的是( )
A. AC=DF B. BC=EF
C. ∠A=∠D D. ∠C=∠F
A
总
结
提
高
这节课你有什么收获?
谢谢大家!
第十二章全等三角形
12.2 全等三角形的判定
第三课时(ASA,AAS)
人教版
八年级上册
学习目标
1.通过动手操作,合作交流、分析、归纳,经历全等三角形的识别方法--“角边角”,“角角边”定理的探索过程,掌握这种识别方法,并会用此定理进行简单的推理;
2.能运用“边角边”,“角角边”定理这个方法证明三角形全等及解决实际问题。
情境
导
入
我们已经知道:三角形全等的判定条件有哪些
“SSS"和“ SAS”。
那除了这两个条件,满足另一些条件的两个三角形是否也可能全等呢
一张教学用的三角形硬纸板不小心被撕坏了(如图所示),你能制作一张与原来同样大小的新教具吗 恢复原来三角形的原貌吗
选取①纸片,
①
②
③
讲
授
新
知
一 探究两角夹边三角形全等
探究3:
先任意画出一个△ABC,再画出一个△A’B'C',使A'B'=AB,∠B’=∠B, ∠A’=∠A(即两角和它们的夹边分别相等).把画好的ΔA'B’C'剪下来,放到△ABC上,它们全等吗
如何用尺规作图,画出一个△A’B'C'?
(1)画A’B’=AB;
(2)在A’B’的同旁画∠DA'B’=∠A,∠EB’A’=∠B,A'D,H'E交于点C’,
ΔA'B'C'就是所要画的三角形
A
B
C
讲
授
新
知
A’
B’
D
E
C’
这个探究结果反快了什么规律 试着说说你的发现
讲
授
新
知
两角和一边分别相等的两个三角形全等,
两角和它们的夹边分别相等的两个三角形全等
两角和它们的夹边分别相等的两个三角形全等(可以简写成"角边角"或“ASA”)
注意,"边"必须是“两角的夹边".
讲
授
新
知
利用今天“边角边”的知识,我们就可以解决课前问题了,现在你会解释了吗
二 运用“角边角”判定方法,解决简单问题
第一块玻璃,因为它完整的保留了两角及夹边,一个角形两个角的大小和它们的夹边的长度确定了,这个三角形的形状、大小就确定下来了。
例3:如图所示,点D在AB上,点E在AC上,AB=AC, ∠B=∠C.求证:AD=AE.
讲
授
新
知
分析:AD和AE分别在△ADC 和△AEB中,所以要证AD=AE,只需证明△ADC≌ΔAEB 即可.
B
C
D
A
E
例3:如图所示,点D在AB上,点E在AC上,AB=AC, ∠B=∠C.求证:AD=AE.
讲
授
新
知
B
C
D
A
E
证明:在△ADC 和△AEB中,
∠A=∠A,
AC=AB,
∠C=∠B,
∴△ADC≌△AEB(ASA)
∴AD=AE.
讲
授
新
知
如图所示,在△ABC和△DEF中,∠A=∠D,∠B=∠E, BC=EF,△ABC 与△DEF 全等吗 能利用角边角条件证明你的结论吗
三 探究两角一边判定三角形全等
看已知条件,能否用“角边角”条件证明
A
B
C
F
E
D
讲
授
新
知
三 探究两角一边判定三角形全等
证明:在ABC中,∠A+∠B+∠C=180°,
∴∠C=180-∠A-∠B,
A
B
C
F
E
D
同理:在DEF中,∴∠F=180°-∠D-∠E,
∵∠A=∠D,∠B=∠E,
∴∠C=∠F,
讲
授
新
知
三 探究两角一边判定三角形全等
A
B
C
F
E
D
证明:在△ABC 和△DEF中,
∠B=∠E,
BC=EF,
∠C=∠F,
∴△ABC≌△DEF(ASA)
讲
授
新
知
三 探究两角一边判定三角形全等
从上面可以看出,从这些已知条件中能得到两个三角形全等,这又反映了一个什么规律?
两角和其中一条边分别相等的两个三角形全等
在"ASA”中“边必须是"两角的夹边”,而这里,边可以是"其中一个角的对边”,强调 “AAS"中的边是"其中一个角的对边"。
这里的"边”是其中一个角对边那怎样更完整地表述这一规律
两角和其中一个角的对边分别相等的两个三角形全等(可以简写成“角角边”或"AAS ”)
讲
授
新
知
四 探究三角分别相等的三角形不全等
三角对应相等的两个三角形全等吗 想想,怎样来探究这个问题?
用两个同一形状,大小不同的三角板
这一规律我们可以怎样表达
有三个角对应相等的两个三角形不一定全等(没有“角角角”或”AAA”)
讲
授
新
知
四 探究三角分别相等的三角形全等
判定两个三角形全等我们已有了哪些方法
SSS,SAS,ASA,AAS.
通过上面的4种判定方法可以看出.至少具备3个条件,才能判定三角形全等 这三个条件有么要求吗
三个条件中必须有边,可以没有角。
1.已知AB=A’B’,∠A=∠A’,∠B=∠B’,则△ABC≌△A’B’C’的依据是( ).
A. SAS B. SSA C.ASA D.AAS
巩
固
应用
C
2. 在△ABC和△DEF中,AB=DE,∠B=∠E, 要使△ABC 与△DEF 全等,则下列补充的条件中错误的是( )
A. AC=DF B. BC=EF
C. ∠A=∠D D. ∠C=∠F
A
总
结
提
高
这节课你有什么收获?
谢谢大家!
