人教版八年级上册12.2 全等三角形的判定(第1课时)(SSS)课件(共24张PPT)
文档属性
| 名称 | 人教版八年级上册12.2 全等三角形的判定(第1课时)(SSS)课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 172.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-12 00:00:00 | ||
图片预览




文档简介
(共24张PPT)
第十二章全等三角形
12.2 全等三角形的判定
第一课时(SSS)
人教版
八年级上册
学习目标
1.构建三角形全等条件的探索思路,体会研究几何问题的方法;
2.探索并理解“边边边”判定方法,会用“边边边”判定方法证明三角形全等;
3.会用尺规作一个角等于已知角,了解作图的道理。
复习
导
入
1.什么叫全等三角形?
2.全等三角形有什么性质?
3.如图所示,已知△ABC≌△A’B’C’,找出其中相等的角和边。
A
B
C
A’
B’
C’
∠A=∠A’,
∠B=∠B’,
∠C=∠C’;
AB=A’B’,
AC=A’C’,
BC= B’C’;
一定要满足三条边分别相等,三个角也分别相等,才能保证两个三角形全等吗?
上述六个条件中,有些条件是相关的,能否在这六个条件中选出部分条件,简洁的判定这两个三角形全等呢?
讲
授
新
知
一 提出“全等判定”问题,构建探索思路
探究1:
任意画一个△ABC,再画一个△A’B’C’,使△ABC与△A’B’C’满足上述六个条件中的一个(一边或一角分别相等)或两个(两边,一边一角或两角分别相等),你画出来的△ABC与△A’B’C’一定全等吗?
当满足一个条件时,△ABC与△A’B’C’全等吗?
讲
授
新
知
一 提出“全等判定”问题,构建探索思路
第一种情况:一条边分别相等;
讲
授
新
知
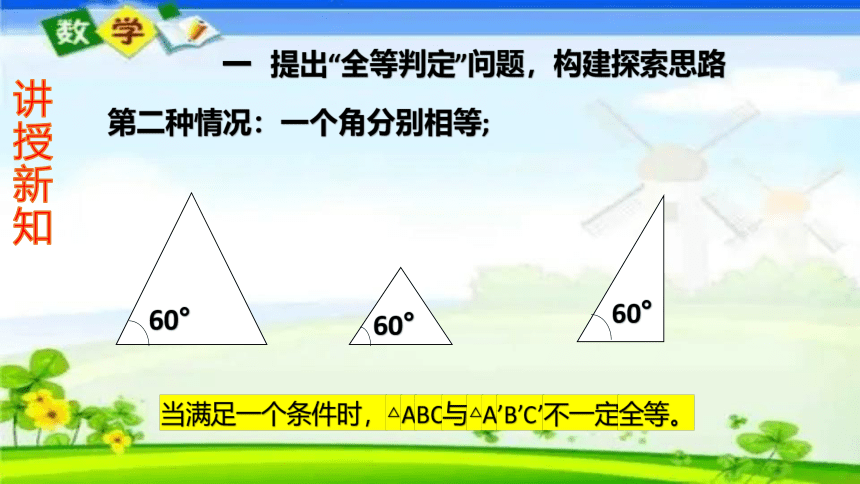
一 提出“全等判定”问题,构建探索思路
第二种情况:一个角分别相等;
60°
60°
60°
当满足一个条件时,△ABC与△A’B’C’不一定全等。
讲
授
新
知
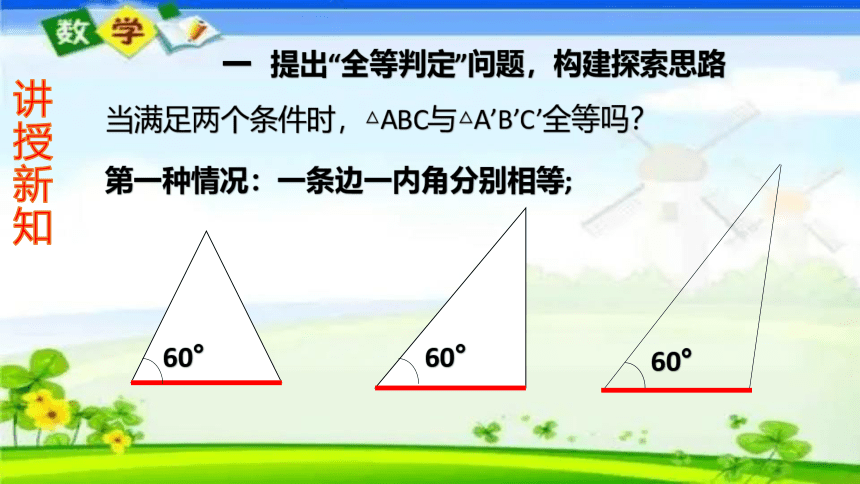
一 提出“全等判定”问题,构建探索思路
当满足两个条件时,△ABC与△A’B’C’全等吗?
第一种情况:一条边一内角分别相等;
60°
60°
60°
讲
授
新
知
一 提出“全等判定”问题,构建探索思路
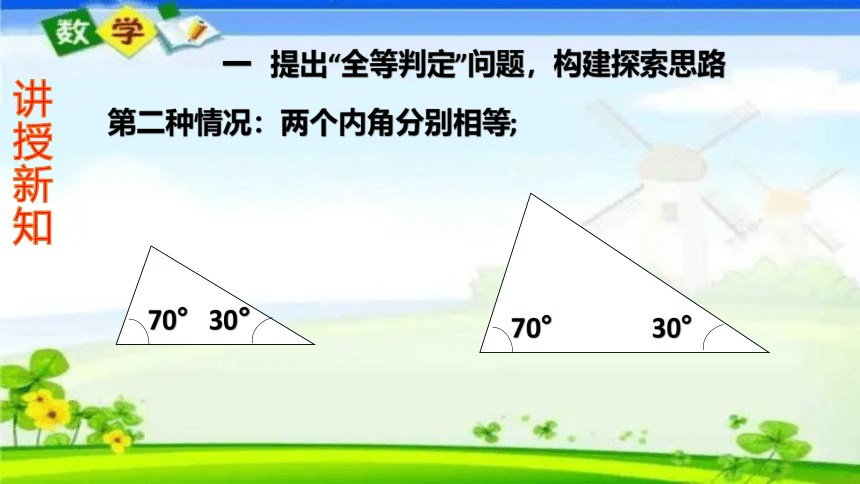
第二种情况:两个内角分别相等;
70°
30°
70°
30°
讲
授
新
知
一 提出“全等判定”问题,构建探索思路
第三种情况:两条边分别相等;
4cm
2cm
4cm
2cm
当满足两个条件时,△ABC与△A’B’C’不一定全等。
思考:
当满足三个条件时,△ABC与△A’B’C’全等吗
满足三个条件时,又分为几种情况?
四种情况:
三边,三角,两边及一角,两角及一边分别相等。
讲
授
新
知
探究二:先任意画一个△ABC,再画一个△A’B’C’,使A’B’=AB,B’C’=BC,A’C’=AC,把画好的△A’B’C’剪下,放到△ABC上,它们全等吗
怎样画一个△A’B’C’?
二 探究“边边边”判定方法.
A
B
C
尺规作图
讲
授
新
知
①画线段A’B’,使A’B’=AB,确定了A’,B’的位置。
A
B
C
如何确定了C’的位置 C’满足什么条件?
A’
B’
B’C’=BC,A’C’=AC,分别以为圆心,线段的长度为半径画弧,两弧交于一点,即为C’。
C’
讲
授
新
知
讲
授
新
知
三边分别相等的两个三角形全等
(简写成“边边边”或“SSS”)
作图的结果反映了什么规律?你能用文字语言和符号语言概括吗?
学习了这个判定定理,如何用符号语言表达呢?
在△ABC和△A’B’C’中,
AB=A’B’,
BC=B’C’,
AC=A’C’,
∴△ABC≌△A’B’C’
讲
授
新
知
例1:如图所示的三角形钢架中,AB=AC,AD是连接点A与BC中点D的支架,求证:△ABD≌△ACD。
三 运用“边边边”判定方法,解决简单问题
A
D
C
B
证明:∵D是BC中点,∴BD=DC,
在△ABD和△ACD中,
BD=DC,
AB=AC,
AD=AD,
∴△ABD≌△ACD
任意画一个∠AOB,能否利用“边边边”判定方法,来画一个∠A’O’B’等于∠AOB?
三 运用“边边边”判定方法,解决简单问题
讲
授
新
知
能否将作一个角等于∠AOB,转化为作一个三角形与∠AOB所在的三角形全等?
B
A
O
D
C
B’
A’
O’
D’
C’
还有其他方法吗
(1)以点O为圆心,任意长为半径画弧,分别交OA,OB为点C,D;
讲
授
新
知
B
A
O
D
C
(2)画一条射线O’A’,以点O’为圆心,OC长为半径画弧,交O’A’于点C’;
讲
授
新
知
B
A
O
D
C
O’
A’
C’
(3)以点C’为圆心,CD长为半径画弧,于第二步所画的弧交于点D’;
讲
授
新
知
B
A
O
D
C
O’
A’
C’
D’
(4)过点D’画射线O’B’,则∠A’O’B’=∠AOB;
讲
授
新
知
B
A
O
D
C
O’
A’
C’
D’
B’
1.如图所示,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是( )
A.120° B.125° C. 127° D.104°
巩
固
应用
C
A
C
D
B
2. 若AB=DE,BC=EF,AC=DF,∠A=50°,∠B=30°,则∠F=( )
100°
3.将三根木条钉成一个三角形木架,这个三角形木架的形状,大小就不变了,当时验证了三角形的稳定性,现在你能解释其中的道理吗?
总
结
提
高
这节课你有什么收获?
谢谢大家!
第十二章全等三角形
12.2 全等三角形的判定
第一课时(SSS)
人教版
八年级上册
学习目标
1.构建三角形全等条件的探索思路,体会研究几何问题的方法;
2.探索并理解“边边边”判定方法,会用“边边边”判定方法证明三角形全等;
3.会用尺规作一个角等于已知角,了解作图的道理。
复习
导
入
1.什么叫全等三角形?
2.全等三角形有什么性质?
3.如图所示,已知△ABC≌△A’B’C’,找出其中相等的角和边。
A
B
C
A’
B’
C’
∠A=∠A’,
∠B=∠B’,
∠C=∠C’;
AB=A’B’,
AC=A’C’,
BC= B’C’;
一定要满足三条边分别相等,三个角也分别相等,才能保证两个三角形全等吗?
上述六个条件中,有些条件是相关的,能否在这六个条件中选出部分条件,简洁的判定这两个三角形全等呢?
讲
授
新
知
一 提出“全等判定”问题,构建探索思路
探究1:
任意画一个△ABC,再画一个△A’B’C’,使△ABC与△A’B’C’满足上述六个条件中的一个(一边或一角分别相等)或两个(两边,一边一角或两角分别相等),你画出来的△ABC与△A’B’C’一定全等吗?
当满足一个条件时,△ABC与△A’B’C’全等吗?
讲
授
新
知
一 提出“全等判定”问题,构建探索思路
第一种情况:一条边分别相等;
讲
授
新
知
一 提出“全等判定”问题,构建探索思路
第二种情况:一个角分别相等;
60°
60°
60°
当满足一个条件时,△ABC与△A’B’C’不一定全等。
讲
授
新
知
一 提出“全等判定”问题,构建探索思路
当满足两个条件时,△ABC与△A’B’C’全等吗?
第一种情况:一条边一内角分别相等;
60°
60°
60°
讲
授
新
知
一 提出“全等判定”问题,构建探索思路
第二种情况:两个内角分别相等;
70°
30°
70°
30°
讲
授
新
知
一 提出“全等判定”问题,构建探索思路
第三种情况:两条边分别相等;
4cm
2cm
4cm
2cm
当满足两个条件时,△ABC与△A’B’C’不一定全等。
思考:
当满足三个条件时,△ABC与△A’B’C’全等吗
满足三个条件时,又分为几种情况?
四种情况:
三边,三角,两边及一角,两角及一边分别相等。
讲
授
新
知
探究二:先任意画一个△ABC,再画一个△A’B’C’,使A’B’=AB,B’C’=BC,A’C’=AC,把画好的△A’B’C’剪下,放到△ABC上,它们全等吗
怎样画一个△A’B’C’?
二 探究“边边边”判定方法.
A
B
C
尺规作图
讲
授
新
知
①画线段A’B’,使A’B’=AB,确定了A’,B’的位置。
A
B
C
如何确定了C’的位置 C’满足什么条件?
A’
B’
B’C’=BC,A’C’=AC,分别以为圆心,线段的长度为半径画弧,两弧交于一点,即为C’。
C’
讲
授
新
知
讲
授
新
知
三边分别相等的两个三角形全等
(简写成“边边边”或“SSS”)
作图的结果反映了什么规律?你能用文字语言和符号语言概括吗?
学习了这个判定定理,如何用符号语言表达呢?
在△ABC和△A’B’C’中,
AB=A’B’,
BC=B’C’,
AC=A’C’,
∴△ABC≌△A’B’C’
讲
授
新
知
例1:如图所示的三角形钢架中,AB=AC,AD是连接点A与BC中点D的支架,求证:△ABD≌△ACD。
三 运用“边边边”判定方法,解决简单问题
A
D
C
B
证明:∵D是BC中点,∴BD=DC,
在△ABD和△ACD中,
BD=DC,
AB=AC,
AD=AD,
∴△ABD≌△ACD
任意画一个∠AOB,能否利用“边边边”判定方法,来画一个∠A’O’B’等于∠AOB?
三 运用“边边边”判定方法,解决简单问题
讲
授
新
知
能否将作一个角等于∠AOB,转化为作一个三角形与∠AOB所在的三角形全等?
B
A
O
D
C
B’
A’
O’
D’
C’
还有其他方法吗
(1)以点O为圆心,任意长为半径画弧,分别交OA,OB为点C,D;
讲
授
新
知
B
A
O
D
C
(2)画一条射线O’A’,以点O’为圆心,OC长为半径画弧,交O’A’于点C’;
讲
授
新
知
B
A
O
D
C
O’
A’
C’
(3)以点C’为圆心,CD长为半径画弧,于第二步所画的弧交于点D’;
讲
授
新
知
B
A
O
D
C
O’
A’
C’
D’
(4)过点D’画射线O’B’,则∠A’O’B’=∠AOB;
讲
授
新
知
B
A
O
D
C
O’
A’
C’
D’
B’
1.如图所示,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是( )
A.120° B.125° C. 127° D.104°
巩
固
应用
C
A
C
D
B
2. 若AB=DE,BC=EF,AC=DF,∠A=50°,∠B=30°,则∠F=( )
100°
3.将三根木条钉成一个三角形木架,这个三角形木架的形状,大小就不变了,当时验证了三角形的稳定性,现在你能解释其中的道理吗?
总
结
提
高
这节课你有什么收获?
谢谢大家!
