二元一次方程组小结[下学期]
文档属性
| 名称 | 二元一次方程组小结[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-20 00:00:00 | ||
图片预览






文档简介
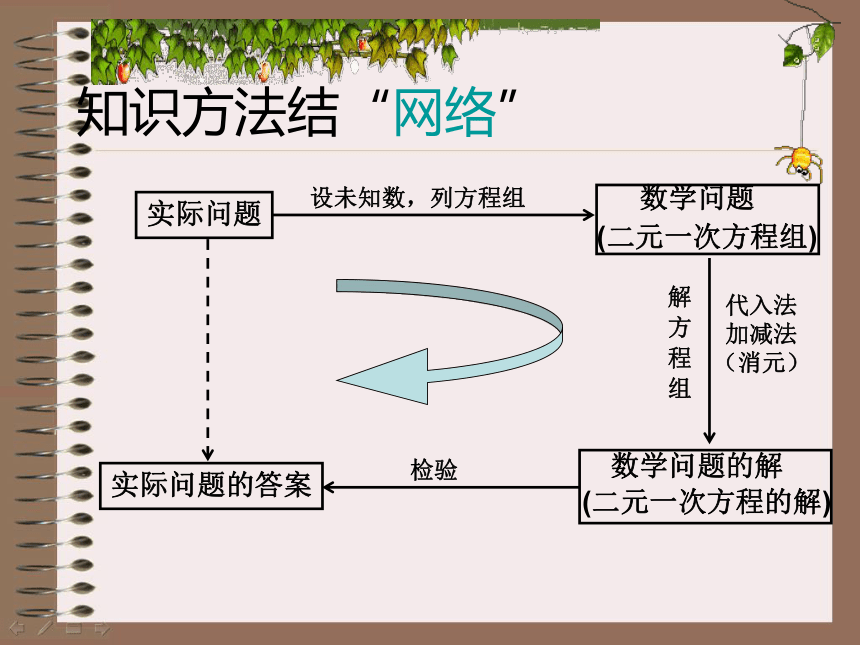
课件15张PPT。 小 结二元一次方程组关于定义3、二元一次方程组的两个方程左、右两边的值都相等的两个未知数的值,叫做二元一次方程组的解1、含有两个未知数,且未知项次数是1的方程,叫做二元一次方程2、含有两个未知数的两个一次方程所组成的一组方程,叫做二元一次方程组关于解法3、解二元一次方程组的步骤是什么?1、解二元一次方程组你有几种方法?两种:代入法和加减法2、代入法和加减法解方程组,“代入”与“加减”的目的是什么?消元:把二元一次方程转化为一元一次方程关于应用在列二元一次方程组解实际问题的过程中,你认为最关键的是什么? 某校七年级组织学生去春游,原计划租用45座车若干辆,但有15人没座;若租用同样数量的60座客车,则多出一辆,且其余客车全部坐满,已知45座客车每日租金每辆220元,60座客车每日租金为每辆300元.(1)七年级由多少?原计划租用45座客车多少辆?(2)若租同一种车,使每位学生都有座,怎样租合算?找出等量关系,列出方程组13、在解方程组时,小张正确的解了方程组中的C 得到方程组的解为试求方程组中的a、b、c的值。探索与思考,小李由于看错实际问题实际问题的答案知识方法结“网络”学习了本节课你有哪些收获?再 见!关于定义2.二元一次方程必须含有两个未知数如y + 3 = 0,3x + 5y + 2z = 0 都不是二元一次方程.3.二元一次方程中的“ 一次”是指含未知数的项的次数,而不是未知数的次数.如方程 xy + 2 = 0,虽然含有两个未知数,而且未知数的次数都是“1”,但整个 xy这一项是二次,所以它不是二元一次方程.关于定义二元一次方程组里一共含有两个未知数,而不是每个方程一定要含有两个未知数.如:关于定义 适合一个二元一次方程的每一对未知数的值,都叫做二元一次方程的一个解.要注意二元一次方程的解是一组数. 如 x =-3,y = -2 就是二元一次方程 x + y = -5 的一个解,写成如下形势
这里要特别注意的是:x = -3 不是方程 x + y = -5
的一个解;y = -2 也不是方程 x + y = -5 的一个
解,只有把它们组合在一起,才是二元一次方程
x + y = -5的一个解.代入消元法的步骤⒈将其中一个方程化为用含一个未知数的代数式表示另一个未知数的形式,如:y=ax+b的形式
⒉将y=ax+b代入另一个方程,消去y,得到一个关于x的一元一次方程;
⒊解关于x的一元一次方程;
⒋将x的值代入y=ax+b中,求出y的值;
⒌检验后写成方程组解的形式。代入法解二元一次方程组x=3 解:由(1)得
x=10+7y (3)
将(3)代入(2)得3(10+7y)+y-8=0
22y=-22
y=-1
把y=-1代入(3)得 x=10+7×(-1)
x=3 注意:检验要使每个方程都成立,检验过程可以省略不写。
解法二:变形(2)也行,一般有一个方程的未知数系数为±1(或没有常数项)的方程组用代入法简单。y=-1是原方程组的解加减消元法的步骤⒈ 使相同未知数的系数相同或相反(若不同 a .成倍数关系,b.不成倍数关系,利用等式的基本性质使之变成相同或相反);
⒉ 利用等式的基本性质将两个方程相加(系数相反)或相减(系数相同),消去一个未知数得到一个一元一次方程;
⒊ 解一元一次方程求出一个未知数的值;
⒋ 将这个未知数的值代入到一个二元一次方程解出另一个未知数的值;
⒌ 检验后写成方程组解的形式.加减法解二元一次方程组解法二:
(1)×2 得6x+4y=8(3)
(2)×3 得6x-12y=48(4)
(3)-(4) 得16y=-40
y=-2.5
把y=-2.5代入(1)得
3x+2×(-2.5)=4
3x=9
x=3解: (1)×2得
6x+4y=8 (3)
(3)+ (2)得
8x=24
x=3
把x=3代入(1)得
2×3-4y=16
-4y=10
y=-2.5
这里要特别注意的是:x = -3 不是方程 x + y = -5
的一个解;y = -2 也不是方程 x + y = -5 的一个
解,只有把它们组合在一起,才是二元一次方程
x + y = -5的一个解.代入消元法的步骤⒈将其中一个方程化为用含一个未知数的代数式表示另一个未知数的形式,如:y=ax+b的形式
⒉将y=ax+b代入另一个方程,消去y,得到一个关于x的一元一次方程;
⒊解关于x的一元一次方程;
⒋将x的值代入y=ax+b中,求出y的值;
⒌检验后写成方程组解的形式。代入法解二元一次方程组x=3 解:由(1)得
x=10+7y (3)
将(3)代入(2)得3(10+7y)+y-8=0
22y=-22
y=-1
把y=-1代入(3)得 x=10+7×(-1)
x=3 注意:检验要使每个方程都成立,检验过程可以省略不写。
解法二:变形(2)也行,一般有一个方程的未知数系数为±1(或没有常数项)的方程组用代入法简单。y=-1是原方程组的解加减消元法的步骤⒈ 使相同未知数的系数相同或相反(若不同 a .成倍数关系,b.不成倍数关系,利用等式的基本性质使之变成相同或相反);
⒉ 利用等式的基本性质将两个方程相加(系数相反)或相减(系数相同),消去一个未知数得到一个一元一次方程;
⒊ 解一元一次方程求出一个未知数的值;
⒋ 将这个未知数的值代入到一个二元一次方程解出另一个未知数的值;
⒌ 检验后写成方程组解的形式.加减法解二元一次方程组解法二:
(1)×2 得6x+4y=8(3)
(2)×3 得6x-12y=48(4)
(3)-(4) 得16y=-40
y=-2.5
把y=-2.5代入(1)得
3x+2×(-2.5)=4
3x=9
x=3解: (1)×2得
6x+4y=8 (3)
(3)+ (2)得
8x=24
x=3
把x=3代入(1)得
2×3-4y=16
-4y=10
y=-2.5
