数学人教A版(2019)选择性必修第三册6.3.1 二项式定理(共20张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第三册6.3.1 二项式定理(共20张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-12 17:26:18 | ||
图片预览








文档简介
(共20张PPT)
二项式定理
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
创设情境,初步体验
不积跬步,无以至千里;
不积小流,无以成江海。
———荀子 ·《劝学篇》
释义:做事情不一点一点积累,就永远无法达成目的。
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
创设情境,初步体验
把自己的起始优秀值看成1,假设每天的努力能让自己变得比前一天优秀1%,对优秀值进行复利计算:
第1天努力后优秀值为________________;
第2天努力后优秀值为________________;
......
第30天努力后优秀值为________________;
1+0.01
(1+0.01)2
(1+0.01)30
估算(1+0.01)30 的近似值(精确到0.1)
TEXT HERE
TEXT HERE
探究归纳,发现规律
思考1:为了探究的展开式,按照由特殊到一般的方法,可以先研究取哪些值的情况呢?
TEXT HERE
探究归纳,发现规律
思考2:能否解释每一组系数与项数?
多项式运算法则
TEXT HERE
探究归纳,发现规律
思考2:能否用计数原理解释每一组系数与项数?
红球 字母
黄球 字母
从中选一个
从中选一个
现有两个装有1个红球,1个黄球的箱子,现从两个箱子中,各摸出一个球。
TEXT HERE
探究归纳,发现规律
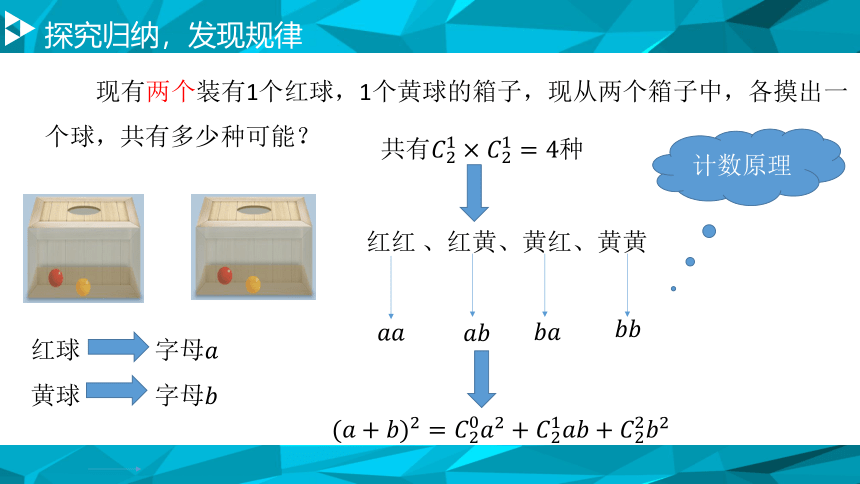
现有两个装有1个红球,1个黄球的箱子,现从两个箱子中,各摸出一个球,共有多少种可能?
红球 字母
黄球 字母
红红 、红黄、黄红、黄黄
计数原理
TEXT HERE
TEXT HERE
探究归纳,发现规律
思考3:不计算,能否运用摸球试验解释?并写出展开式?
三个箱子均取到红球
3个不选
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
探究归纳,发现规律
思考4: 通过刚才的推导方式,对于是否适用,若适用,请尝试写出各项
TEXT HERE
知识建构,形成定理
思考5:请按照上述的方法与规律,猜想的展开式。
二项式定理
的展开式
展开式的通项
展开式的第
系数
TEXT HERE
知识建构,形成定理
对于猜想 我们如何进行证明呢?
证明:
是个 相乘,每个 在相乘时,两种选择,选或选
由分步计数原理可知: 展开式共有 项(包括同类项),
其中每一项都是 的形式,对于每一项
由个 选了, 个 选了得到的,
它出现的次数相当于从个 中取个的组合数 ,
将它们合并同类项,就得二项展开式,这就是二项式定理。
TEXT HERE
知识建构,形成定理
二项式定理,又称牛顿二项式定理,由艾萨克·牛顿于1664年、1665年间提出。该定理给出:两个数之和的整数次幂诸如展开为类似项之和的恒等式。二项式定理可以推广到任意实数次幂,即广义二项式定理。
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
知识建构,形成定理
思考6:(1)展开式有多少项?
(2)每项次数是多少?
(3)展开式中的次数排列规律分别是什么?
(4)二项式系数是多少?
(5)通项是展开式的第几项?
字母a按降幂排列,字母b按照升幂排列,二者指数之和是二项式指数;
第
项
每项次数和为
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
知识建构,形成定理
思考7:小组讨论,尝试写出的展开式。
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
知识迁移,初步应用
例1. 求 的展开式。
解
分析
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
知识迁移,初步应用
例2. 求 的展开式的第三项、二项式系数、项的系数。
变式:求 的展开式的第三项、二项式系数、项的系数。
解:
项的系数
二项式系数
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
知识迁移,初步应用
3. 估算的近似值(精确到0.1)。
变式:估算的近似值(精确到0.1) 。
结论:我们每天努力1%,30天后,比现在优秀30%
解:
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
回顾反思,归纳总结
本节课你收获了什么?二项式定理是怎样得到的?
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
布置作业,课后巩固
必做题:课后练习4、5题
选做题:课后练习 6题
阅读题:查阅二项式定理的数学史
恳请老师和各位同学批评指正
二项式定理
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
创设情境,初步体验
不积跬步,无以至千里;
不积小流,无以成江海。
———荀子 ·《劝学篇》
释义:做事情不一点一点积累,就永远无法达成目的。
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
创设情境,初步体验
把自己的起始优秀值看成1,假设每天的努力能让自己变得比前一天优秀1%,对优秀值进行复利计算:
第1天努力后优秀值为________________;
第2天努力后优秀值为________________;
......
第30天努力后优秀值为________________;
1+0.01
(1+0.01)2
(1+0.01)30
估算(1+0.01)30 的近似值(精确到0.1)
TEXT HERE
TEXT HERE
探究归纳,发现规律
思考1:为了探究的展开式,按照由特殊到一般的方法,可以先研究取哪些值的情况呢?
TEXT HERE
探究归纳,发现规律
思考2:能否解释每一组系数与项数?
多项式运算法则
TEXT HERE
探究归纳,发现规律
思考2:能否用计数原理解释每一组系数与项数?
红球 字母
黄球 字母
从中选一个
从中选一个
现有两个装有1个红球,1个黄球的箱子,现从两个箱子中,各摸出一个球。
TEXT HERE
探究归纳,发现规律
现有两个装有1个红球,1个黄球的箱子,现从两个箱子中,各摸出一个球,共有多少种可能?
红球 字母
黄球 字母
红红 、红黄、黄红、黄黄
计数原理
TEXT HERE
TEXT HERE
探究归纳,发现规律
思考3:不计算,能否运用摸球试验解释?并写出展开式?
三个箱子均取到红球
3个不选
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
探究归纳,发现规律
思考4: 通过刚才的推导方式,对于是否适用,若适用,请尝试写出各项
TEXT HERE
知识建构,形成定理
思考5:请按照上述的方法与规律,猜想的展开式。
二项式定理
的展开式
展开式的通项
展开式的第
系数
TEXT HERE
知识建构,形成定理
对于猜想 我们如何进行证明呢?
证明:
是个 相乘,每个 在相乘时,两种选择,选或选
由分步计数原理可知: 展开式共有 项(包括同类项),
其中每一项都是 的形式,对于每一项
由个 选了, 个 选了得到的,
它出现的次数相当于从个 中取个的组合数 ,
将它们合并同类项,就得二项展开式,这就是二项式定理。
TEXT HERE
知识建构,形成定理
二项式定理,又称牛顿二项式定理,由艾萨克·牛顿于1664年、1665年间提出。该定理给出:两个数之和的整数次幂诸如展开为类似项之和的恒等式。二项式定理可以推广到任意实数次幂,即广义二项式定理。
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
知识建构,形成定理
思考6:(1)展开式有多少项?
(2)每项次数是多少?
(3)展开式中的次数排列规律分别是什么?
(4)二项式系数是多少?
(5)通项是展开式的第几项?
字母a按降幂排列,字母b按照升幂排列,二者指数之和是二项式指数;
第
项
每项次数和为
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
知识建构,形成定理
思考7:小组讨论,尝试写出的展开式。
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
知识迁移,初步应用
例1. 求 的展开式。
解
分析
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
知识迁移,初步应用
例2. 求 的展开式的第三项、二项式系数、项的系数。
变式:求 的展开式的第三项、二项式系数、项的系数。
解:
项的系数
二项式系数
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
知识迁移,初步应用
3. 估算的近似值(精确到0.1)。
变式:估算的近似值(精确到0.1) 。
结论:我们每天努力1%,30天后,比现在优秀30%
解:
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
回顾反思,归纳总结
本节课你收获了什么?二项式定理是怎样得到的?
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE
TEXT HERE TEXT HERE
TEXT HERE TEXT HERE
布置作业,课后巩固
必做题:课后练习4、5题
选做题:课后练习 6题
阅读题:查阅二项式定理的数学史
恳请老师和各位同学批评指正
