人教版九年级上册 24.2.2直线和圆的位置关系课件(共59张PPT)
文档属性
| 名称 | 人教版九年级上册 24.2.2直线和圆的位置关系课件(共59张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-12 14:28:54 | ||
图片预览







文档简介
(共59张PPT)
海平面
海平面
24.2.2 直线与圆的位置关系
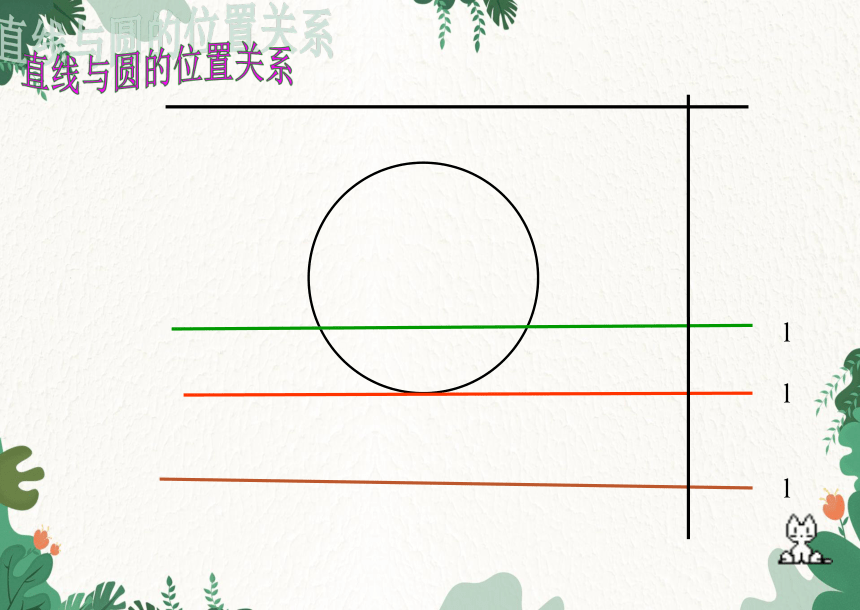
想想:
直线和圆的位置有
何关系???
l
l
l
a
.O
图 1
b
.A
.O
图 2
c
.
F
.E
.O
图 3
这时直线叫做圆的割线 ,
公共点叫直线与圆的交点。
直线与圆没有公共点时,叫做直线与圆相离.
直线与圆有唯一公共点时,叫做直线与圆相切.
直线与圆有两个公共点时,叫做直线与圆相交.
这时直线叫做圆的切线 ,
唯一公共点叫做直线与圆的切点。
1.直线与圆的位置关系 (图形特征)
数量特征
直线与圆有第四种关系吗?
即直线与圆是否有第三个交点?
小问题:
如何根据基本概念来判断直线与圆的位置关系?
根据直线与圆的公共点的个数
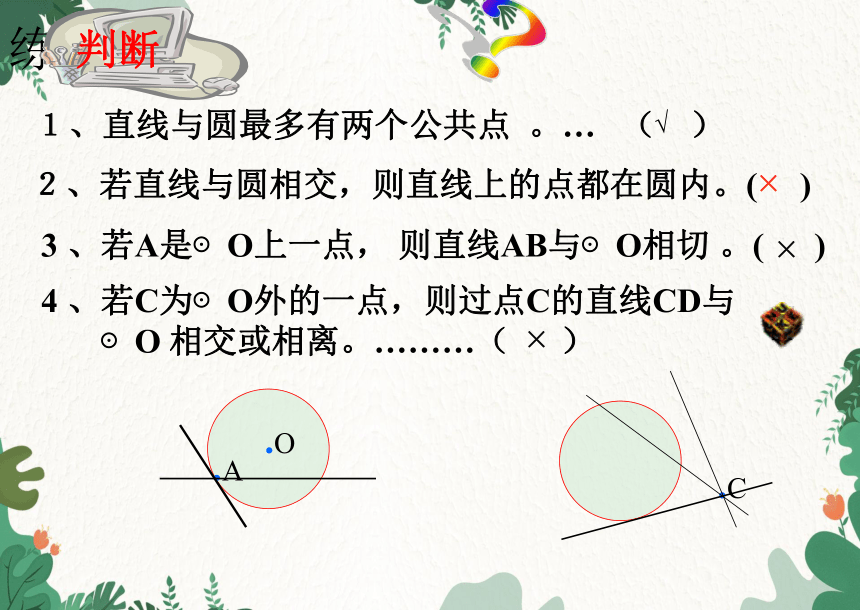
练习1
1、直线与圆最多有两个公共点 。… ( )
√
×
判断
3 、若A是⊙O上一点, 则直线AB与⊙O相切 。( )
.A
.O
2、若直线与圆相交,则直线上的点都在圆内。( )
4 、若C为⊙O外的一点,则过点C的直线CD与
⊙O 相交或相离。………( )
×
×
.C
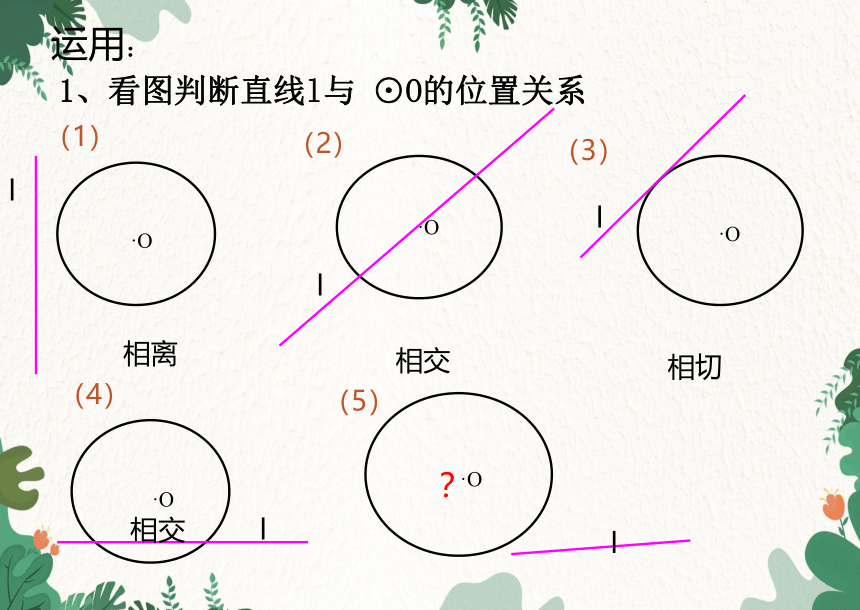
运用:
1、看图判断直线l与 ⊙O的位置关系
(1)
(2)
(3)
(4)
(5)
相离
相切
相交
相交
?
l
l
l
l
l
·O
·O
·O
·O
·O
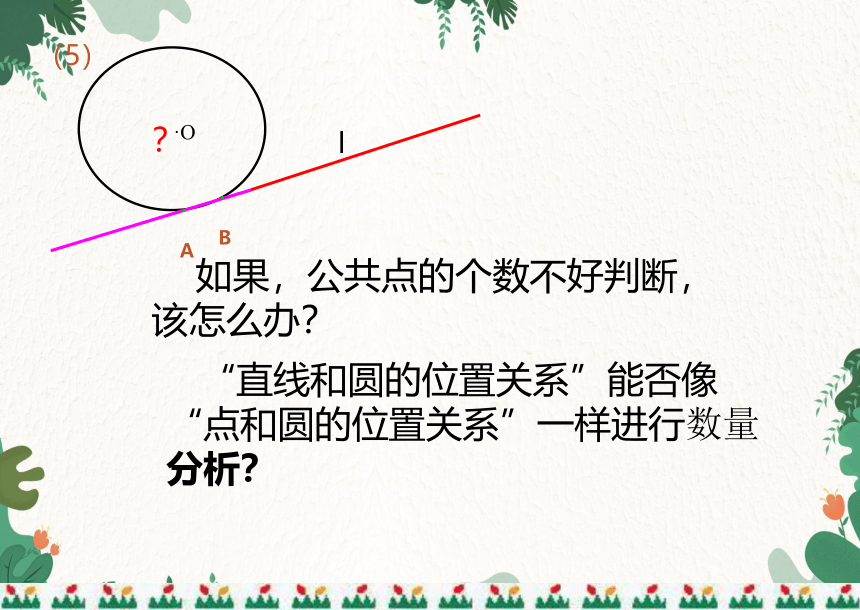
(5)
?
l
如果,公共点的个数不好判断,该怎么办?
·O
“直线和圆的位置关系”能否像“点和圆的位置关系”一样进行数量分析?
·
A
·
B
知识回顾:
.A
. B
C.
.O
3、如何根据圆心到点的距离d与半径r的
关系判别点与圆的位置关系?
1、什么叫点到直线的距离
2、连结直线外一点与直线上所有点
的线段中,最短的是______?
直线外一点到这条直线 的
垂线段的长度叫点到直线 的距离。
垂线段
1、点到圆心的距离___于半径时,点在圆外。
2、点到圆心的距离__于半径时,点在圆上。
3、点到圆心的距离___于半径时,点在圆内。
.E
.
D
a
大
等
小
d
d
d
.O
.O
.O
r
r
r
相离
相切
相交
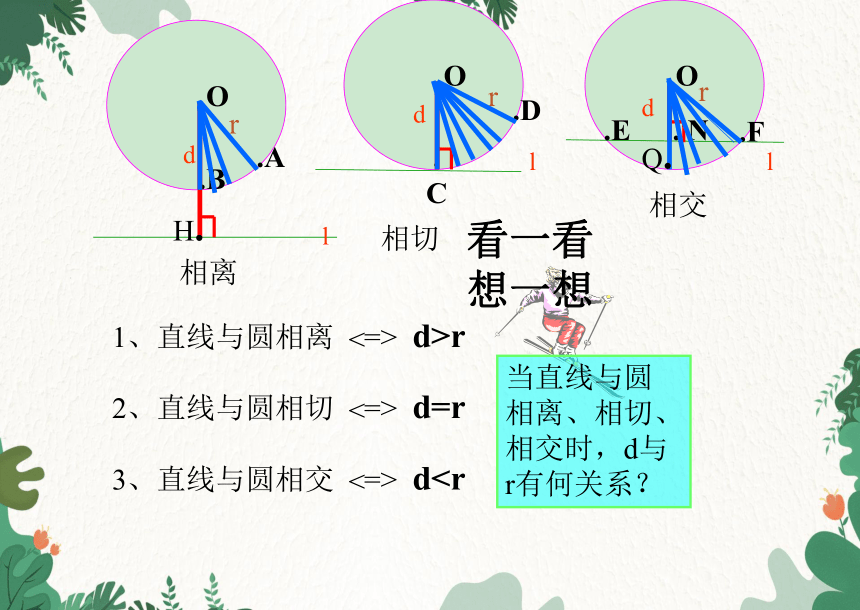
1、直线与圆相离 => d>r
2、直线与圆相切 => d=r
3、直线与圆相交 => d<
<
<
看一看想一想
当直线与圆
相离、相切、
相交时,d与
r有何关系?
l
l
l
.A
.B
.
C
.D
.E
.F
. N
H.
Q.
<
<
<
d
r
相离
.A
d
r
相切
l
l
H.
1、直线与圆相离 => d>r
2、直线与圆相切 => d=r
3、直线与圆相交 => d2.直线与圆的位置关系 (数量特征)
.D
.O
r
d
相交
.
C
.O
.B
直线与圆的位置关系的识别与特征
.
E
.F
O
总结:
判定直线 与圆的位置关系的方法有____种:
(1)根据定义,由________________
的个数来判断;
(2)根据性质,由_________________ 的关系来判断。
在实际应用中,常采用第二种方法判定。
两
直线 与圆的公共点
圆心到直线的距离d与半径r
圆的直径是13cm,如果直线与圆心的距离分别是
(1)4.5cm ; (2) 6.5cm ; (3) 8cm,
那么直线与圆分别是什么位置关系? 有几个公共点?
(3)圆心距 d=8cm>r = 6.5cm 直线与圆相离,
有两个公共点;
有一个公共点;
没有公共点.
A
B
·
6.5cm
d=4.5cm
O
M
(2)圆心距 d=6.5cm = r = 6.5cm 直线与圆相切,
·
N
O
6.5cm
d=6.5cm
解 (1) 圆心距 d=4.5cm< r = 6.5cm 直线与圆相交,
D
·
O
6.5cm
d=8cm
例题1:
练习1: 设⊙O的半径为r,直线a上一点到圆心的距离为d,若d=r,则直线a与⊙O的位置关系是( )
(A)相交 (B)相切 (C)相离 (D)相切或相交
D
练习2:已知圆的半径等于5,直线l与圆没有交点,则圆心到直线的距离d的取值范围是 .
练习3:直线l与半径为r的⊙O相交,且点O到直线l的距离为8,则r的取值范围是 .
d>5
r>8
思考:圆心A到X轴、
Y轴的距离各是多少
例题2:
O
X
Y
已知⊙A的直径为6,点A的坐标为(-3,-4),则⊙A与X轴的位置关系是_____,⊙A与Y轴的位置关系是______。
B
C
4
3
相离
相切
.A
即圆心C到AB的距离d=2.4cm。
(1)当r=2cm时, ∵d>r,
∴⊙C与AB相离。
(2)当r=2.4cm时,∵d=r,
∴⊙C与AB相切。
(3)当r=3cm时, ∵d<r,
∴⊙C与AB相交。
解:过C作CD⊥AB,垂足为D。
在Rt△ABC中,
AB= =
=5(cm)
根据三角形面积公式有
CD·AB=AC·BC
∴CD= =
2
2
2
2
=2.4(cm)。
A
B
C
A
D
4
5
3
d=2.4
例: Rt△ABC,∠C=90°AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?
(1)r=2cm;(2)r=2.4cm
(3)r=3cm。
解后思
在Rt△ABC中,∠C=90°,AC=3cm,
BC=4cm,以C为圆心,r为半径作圆。
1、当 r 满足____________时,⊙C与直线AB相离。
2、当 r 满足___________ 时,⊙C与直线AB相切。
3、当 r 满足_________ 时,
⊙C与直线AB相交。
B
C
A
D
4
5
d=2.4cm
3
4、当 r 满足 ________ 时,
⊙C与线段AB只有一个公共点.
1、如图,已知∠AOB=30°,M为OB上一点,且OM=5cm,以M为圆心、以r为半径的圆与直线OA有怎样的位置关系?为什么 ? ⑴ r =2cm; ⑵ r =4cm; ⑶ r =2.5cm。
O
A
B
M
解:过点M作MC⊥OA于C ,
∵ ∠AOB=30°, OM=5cm, ∴ MC=2.5cm
C
⑴ ∵ d=MC=2.5, r=2 即d >r
∴ ⊙O与OA相离;
⑵ ∵ d=MC=2.5, r=4 即d < r
∴ ⊙O与OA相交;
⑶ ∵ d=MC=2.5, r=2.5 即d= r
∴ ⊙O与OA相切.
.
直线与圆的位置关系
直线与圆的
位置关系 相交 相切 相离
公 共 点
个 数
公 共 点
名 称
直 线
名 称
图 形
圆心到直线距离d与半径r的关系
dd=r
d>r
2
交点
割线
1
切点
切线
0
无
无
1.当你在下雨天快速转动雨伞时水飞出的方向是什么方向?
2.砂轮打磨工件飞出火星的方向是什么方向?
问题
1.直线和圆有哪些位置关系?
2.什么叫做切线?
3.你已经学会了哪些判断一条直线是圆的切线的方法?
图(1)
图(2)
图(3)
O
O
O
复习
观察、提出问题、分析发现
根据切线的定义可以判定一条直线是不是圆的切线,但有时使用定义判定很不方便.我们从另一个侧面去观察,那就是直线和圆的位置怎样时,直线也是圆的切线呢
图(2)中直线l是⊙O的切线,怎样判定?
图(1)
图(2)
图(3)
O
O
O
O
请在⊙O上任意取一点A,连接OA。过点A作直线 l⊥OA。思考一下问题:
1. 圆心O到直线l的距离和圆的半径有什么数量关系
2. 二者位置有什么关系?为什么?
3. 由此你发现了什么?
l
A
发现:(1)直线 l 经过半径OA的外端点A;
(2)直线l垂直于半径0A.
则:直线l与⊙O相切
这样我们就得到了从位置上来判定直线是圆的切线的方法——切线的判定定理.
A
O
l
直线与圆相切的判定定理:
经过半径的外端并且垂直这条半径的直线是圆的切线。
对定理的理解:
切线需满足两条: ①经过半径外端;
②垂直于这条半径.
判 断
1. 过半径的外端的直线是圆的切线( )
2. 与半径垂直的的直线是圆的切线( )
3. 过半径的端点与半径垂直的直线是圆的切线( )
×
×
×
O
r
l
A
O
r
l
A
O
r
l
A
问题:定理中的两个条件缺少一个行不行
两个条件,缺一不可
O
r
l
A
如图所示
∵ OA是半径, l ⊥ OA于A
∴ l是⊙O的切线。
定理的几何符号表达:
切线的判定方法有三种:
①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
③切线的判定定理.即
经过半径的外端并且垂直这条半径的直线是圆的切线
判定直线与圆相切有哪些方法?
例1 直线AB经过⊙O上的点C,并且OA=OB,CA=CB,
求证:直线AB是⊙O的切线.
证明: 连接OC
∵OA=OB, CA=CB
∴△OAB是等腰三角形,OC
是底边AB上的中线
∴OC⊥AB
∴AB是⊙O的切线
B
A
E
D
C
O
例:如图: ⊙O的直径AB=4, ∠ABC=30°,BC=4 ,D是线段BC的中点。
(1)试判断点D与⊙O的位置关系
(2)过点D作DE⊥AC,垂足为点E,求证:直线DE是⊙O的切线
3
A
B
l
O
圆O与直线l相切,则过点A的直径A B与切线l有
怎样的位置关系?
垂直
.
O
A
L
将上页思考中的问题
反过来,如果L是⊙O
的切线,切点为A,那么
半径OA与直线L是不
是一定垂直呢
一定垂直
切线的性质定理:
圆的切线垂直于过切点的半径
A
B
C
D
O
例:如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,求证:AC平分∠DAB
A
B
O
D
C
例:已知:AB是⊙O的直径,BC是⊙O切线,切点为B,OC平行于弦AD,求证:DC是⊙O的切线。
探 究 活 动
如图,纸上有一⊙O ,PA为⊙O的一条切线,沿着直线PO对折,设圆上与点A重合的点为B。
1、OB是⊙O的一条半径吗?
2、PB是⊙O的切线吗?
5、利用图形轴对称性解释
3、PA、PB有何关系?
4、∠APO和∠ BPO有何关系?
A
O
P
P
A
O
B
经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长。
如图,P是⊙O外一点,PA,PB是⊙O的两条切线,我们把线段PA,PB的长叫做点P到⊙O的切线长。
O
P
A
B
切线和切线长是两个不同的概念,
切线是直线,不能度量;
切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量。
O
P
A
B
O
P
A
B
∟
∟
M
根据你的直观判断,猜想图中PA是否等于PB?∠1与∠2又有什么关系?
大胆猜想:
⌒
⌒
1
2
证明:
∵PA、PB是⊙o的两条切线,
∴OA⊥AP,OB⊥BP
又OA=OB,OP=OP,
∴Rt△AOP≌Rt△BOP(HL)∴PA=PB,∠1=∠2
关键是作辅助线~
切线长定理:
从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
O
P
A
B
已知:⊙O的半径为3厘米,点P和圆心O的距离为6厘米,经过点P和⊙O的两条切线,求这两条切线的夹角及切线长.
练习一
O
F
P
E
⌒
1
2
⌒
切线长定理的拓展
B
O
P
A
H
D
C
想一想:根据图形,
你还可以得到什么结论?
平分切点所成的两弧;垂直平分切点所成的弦.
P
A
B
C
O
如AC为直径,观察OP与BC的位置关系,并给予证明。
巩固练习:
(1)已知OA=3cm,OP=6cm,则PA=——,∠APB=——
3√3
60°
(2)OP交⊙O于M,则——————,AB与OP有何关系?
AM=BM
⌒
⌒
M
已知:如图,PA、PB是⊙O的切线,切点分别是A、B,Q为AB上一点,过Q点作⊙O的切线,交PA、PB于E、F点,已知PA=12CM,∠P=70
求:△PEF的周长。
E
A
Q
P
F
B
O
思考
如图,一张三角形的铁皮,如何在它上面截下
一块圆形的用料,并且使圆的面积尽可能大呢
I
D
内切圆和内心的定义:
与三角形各边都相切的圆叫做三角形的内切圆.
内切圆的圆心是三角形三条角平分线的交点,叫
做三角形的内心.
例2 △ABC的内切圆⊙O与BC、CA、AB分别相切于
点D、E、F,且AB=9cm,BC=14cm,CA=13cm,
求AF、BD、CE的长.
解:
设AF=x(cm),则AE=x(cm)
∴CD=CE=AC-AE=13-x
BD=BF=AB-AF=9-x
由 BD+CD=BC可得
(13-x)+(9-x)=14
解得 x=4
∴ AF=4(cm), BD=5(cm), CE=9(cm).
练 习 1
如图,△ABC中,∠ ABC=50°,∠ACB=75 °,点O
是⊙O的内心,求∠ BOC的度数。
A
O
C
B
解:∵点O是⊙O的内心
∴∠OBC=1/2∠ABC=25°
∠OCB=1/2∠ACB=37.5°
∴ ∠BOC=180°﹣25°﹣37.5°
=117.5°
练 习 2
△ABC的内切圆半径为 r , △ABC的周长为 l ,求△ABC
的面积。 (提示:设内心为O,连接OA、OB、OC。)
O
A
C
B
r
解:连接OA、OB、OC,则
S= AB × r + AC × r + BC × r
= (AB +AC+BC) × r
= l r
r
r
r
记忆:
1. Rt△ABC中,∠C=90°,a=3,b=4,则内切圆的半径是_______.
1
练习1.在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,以D为
圆心,DB长为半径作⊙D.试说明:AC是⊙D的切线.
F
2.AB是⊙O的弦,C是⊙O外一点,BC是⊙O的切线,AB交
过C点的直径于点D,OA⊥CD,试判断△BCD的形状,并
说明你的理由.
3.AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过点E
作⊙O的切线交AC于点D,试判断△AED的形状,并
说明理由.
基础题:
1.既有外接圆,又内切圆的平行四边形是______.
2.直角三角形的外接圆半径为5cm,内切圆半径为1cm,
则此三角形的周长是_______.
3.⊙O边长为2cm的正方形ABCD的内切圆,E、F切⊙O
于P点,交AB、BC于E、F,则△BEF的周长是_____.
E
F
H
G
正方形
22cm
2cm
4.已知:三角形ABC内接于⊙O,过点A作直线EF.
(1)图甲,AB为直径,要使得EF是⊙O切线,还需添加的条件
(只需写出三种情况)①___________②_____________
③______________.
(2)图乙, AB为非直径的弦,∠CAE=∠B.求证:EF是⊙O的
切线.
∠CAE=∠B
AB⊥FE
∠BAC+∠CAE=90°
H
5.小红家的锅盖坏了,为了配一个锅盖,需要测量锅盖的
直径(锅边所形成的圆的直径),而小红家只有一把长20cm
的直尺,根本不够长,怎么办呢 小红想了想,采取以下方
法:首先把锅平放到墙根,锅边刚好靠到两墙,用直尺紧贴
墙面量得MA的长,即可求出墙的直径,请你利用图乙,说
明她这样做的道理.
6.已知直角梯形 ABCD 中,AD∥BC,AB⊥BC,以腰DC的中点 E 为圆心的圆与 AB 相切,梯形的上底 AD 与底 BC 是方程 x 2-10x + 16 = 0 的两根,求 ⊙E 的半径 r .
F
海平面
海平面
24.2.2 直线与圆的位置关系
想想:
直线和圆的位置有
何关系???
l
l
l
a
.O
图 1
b
.A
.O
图 2
c
.
F
.E
.O
图 3
这时直线叫做圆的割线 ,
公共点叫直线与圆的交点。
直线与圆没有公共点时,叫做直线与圆相离.
直线与圆有唯一公共点时,叫做直线与圆相切.
直线与圆有两个公共点时,叫做直线与圆相交.
这时直线叫做圆的切线 ,
唯一公共点叫做直线与圆的切点。
1.直线与圆的位置关系 (图形特征)
数量特征
直线与圆有第四种关系吗?
即直线与圆是否有第三个交点?
小问题:
如何根据基本概念来判断直线与圆的位置关系?
根据直线与圆的公共点的个数
练习1
1、直线与圆最多有两个公共点 。… ( )
√
×
判断
3 、若A是⊙O上一点, 则直线AB与⊙O相切 。( )
.A
.O
2、若直线与圆相交,则直线上的点都在圆内。( )
4 、若C为⊙O外的一点,则过点C的直线CD与
⊙O 相交或相离。………( )
×
×
.C
运用:
1、看图判断直线l与 ⊙O的位置关系
(1)
(2)
(3)
(4)
(5)
相离
相切
相交
相交
?
l
l
l
l
l
·O
·O
·O
·O
·O
(5)
?
l
如果,公共点的个数不好判断,该怎么办?
·O
“直线和圆的位置关系”能否像“点和圆的位置关系”一样进行数量分析?
·
A
·
B
知识回顾:
.A
. B
C.
.O
3、如何根据圆心到点的距离d与半径r的
关系判别点与圆的位置关系?
1、什么叫点到直线的距离
2、连结直线外一点与直线上所有点
的线段中,最短的是______?
直线外一点到这条直线 的
垂线段的长度叫点到直线 的距离。
垂线段
1、点到圆心的距离___于半径时,点在圆外。
2、点到圆心的距离__于半径时,点在圆上。
3、点到圆心的距离___于半径时,点在圆内。
.E
.
D
a
大
等
小
d
d
d
.O
.O
.O
r
r
r
相离
相切
相交
1、直线与圆相离 => d>r
2、直线与圆相切 => d=r
3、直线与圆相交 => d
<
<
看一看想一想
当直线与圆
相离、相切、
相交时,d与
r有何关系?
l
l
l
.A
.B
.
C
.D
.E
.F
. N
H.
Q.
<
<
<
d
r
相离
.A
d
r
相切
l
l
H.
1、直线与圆相离 => d>r
2、直线与圆相切 => d=r
3、直线与圆相交 => d
.D
.O
r
d
相交
.
C
.O
.B
直线与圆的位置关系的识别与特征
.
E
.F
O
总结:
判定直线 与圆的位置关系的方法有____种:
(1)根据定义,由________________
的个数来判断;
(2)根据性质,由_________________ 的关系来判断。
在实际应用中,常采用第二种方法判定。
两
直线 与圆的公共点
圆心到直线的距离d与半径r
圆的直径是13cm,如果直线与圆心的距离分别是
(1)4.5cm ; (2) 6.5cm ; (3) 8cm,
那么直线与圆分别是什么位置关系? 有几个公共点?
(3)圆心距 d=8cm>r = 6.5cm 直线与圆相离,
有两个公共点;
有一个公共点;
没有公共点.
A
B
·
6.5cm
d=4.5cm
O
M
(2)圆心距 d=6.5cm = r = 6.5cm 直线与圆相切,
·
N
O
6.5cm
d=6.5cm
解 (1) 圆心距 d=4.5cm< r = 6.5cm 直线与圆相交,
D
·
O
6.5cm
d=8cm
例题1:
练习1: 设⊙O的半径为r,直线a上一点到圆心的距离为d,若d=r,则直线a与⊙O的位置关系是( )
(A)相交 (B)相切 (C)相离 (D)相切或相交
D
练习2:已知圆的半径等于5,直线l与圆没有交点,则圆心到直线的距离d的取值范围是 .
练习3:直线l与半径为r的⊙O相交,且点O到直线l的距离为8,则r的取值范围是 .
d>5
r>8
思考:圆心A到X轴、
Y轴的距离各是多少
例题2:
O
X
Y
已知⊙A的直径为6,点A的坐标为(-3,-4),则⊙A与X轴的位置关系是_____,⊙A与Y轴的位置关系是______。
B
C
4
3
相离
相切
.A
即圆心C到AB的距离d=2.4cm。
(1)当r=2cm时, ∵d>r,
∴⊙C与AB相离。
(2)当r=2.4cm时,∵d=r,
∴⊙C与AB相切。
(3)当r=3cm时, ∵d<r,
∴⊙C与AB相交。
解:过C作CD⊥AB,垂足为D。
在Rt△ABC中,
AB= =
=5(cm)
根据三角形面积公式有
CD·AB=AC·BC
∴CD= =
2
2
2
2
=2.4(cm)。
A
B
C
A
D
4
5
3
d=2.4
例: Rt△ABC,∠C=90°AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?
(1)r=2cm;(2)r=2.4cm
(3)r=3cm。
解后思
在Rt△ABC中,∠C=90°,AC=3cm,
BC=4cm,以C为圆心,r为半径作圆。
1、当 r 满足____________时,⊙C与直线AB相离。
2、当 r 满足___________ 时,⊙C与直线AB相切。
3、当 r 满足_________ 时,
⊙C与直线AB相交。
B
C
A
D
4
5
d=2.4cm
3
4、当 r 满足 ________ 时,
⊙C与线段AB只有一个公共点.
1、如图,已知∠AOB=30°,M为OB上一点,且OM=5cm,以M为圆心、以r为半径的圆与直线OA有怎样的位置关系?为什么 ? ⑴ r =2cm; ⑵ r =4cm; ⑶ r =2.5cm。
O
A
B
M
解:过点M作MC⊥OA于C ,
∵ ∠AOB=30°, OM=5cm, ∴ MC=2.5cm
C
⑴ ∵ d=MC=2.5, r=2 即d >r
∴ ⊙O与OA相离;
⑵ ∵ d=MC=2.5, r=4 即d < r
∴ ⊙O与OA相交;
⑶ ∵ d=MC=2.5, r=2.5 即d= r
∴ ⊙O与OA相切.
.
直线与圆的位置关系
直线与圆的
位置关系 相交 相切 相离
公 共 点
个 数
公 共 点
名 称
直 线
名 称
图 形
圆心到直线距离d与半径r的关系
d
d>r
2
交点
割线
1
切点
切线
0
无
无
1.当你在下雨天快速转动雨伞时水飞出的方向是什么方向?
2.砂轮打磨工件飞出火星的方向是什么方向?
问题
1.直线和圆有哪些位置关系?
2.什么叫做切线?
3.你已经学会了哪些判断一条直线是圆的切线的方法?
图(1)
图(2)
图(3)
O
O
O
复习
观察、提出问题、分析发现
根据切线的定义可以判定一条直线是不是圆的切线,但有时使用定义判定很不方便.我们从另一个侧面去观察,那就是直线和圆的位置怎样时,直线也是圆的切线呢
图(2)中直线l是⊙O的切线,怎样判定?
图(1)
图(2)
图(3)
O
O
O
O
请在⊙O上任意取一点A,连接OA。过点A作直线 l⊥OA。思考一下问题:
1. 圆心O到直线l的距离和圆的半径有什么数量关系
2. 二者位置有什么关系?为什么?
3. 由此你发现了什么?
l
A
发现:(1)直线 l 经过半径OA的外端点A;
(2)直线l垂直于半径0A.
则:直线l与⊙O相切
这样我们就得到了从位置上来判定直线是圆的切线的方法——切线的判定定理.
A
O
l
直线与圆相切的判定定理:
经过半径的外端并且垂直这条半径的直线是圆的切线。
对定理的理解:
切线需满足两条: ①经过半径外端;
②垂直于这条半径.
判 断
1. 过半径的外端的直线是圆的切线( )
2. 与半径垂直的的直线是圆的切线( )
3. 过半径的端点与半径垂直的直线是圆的切线( )
×
×
×
O
r
l
A
O
r
l
A
O
r
l
A
问题:定理中的两个条件缺少一个行不行
两个条件,缺一不可
O
r
l
A
如图所示
∵ OA是半径, l ⊥ OA于A
∴ l是⊙O的切线。
定理的几何符号表达:
切线的判定方法有三种:
①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
③切线的判定定理.即
经过半径的外端并且垂直这条半径的直线是圆的切线
判定直线与圆相切有哪些方法?
例1 直线AB经过⊙O上的点C,并且OA=OB,CA=CB,
求证:直线AB是⊙O的切线.
证明: 连接OC
∵OA=OB, CA=CB
∴△OAB是等腰三角形,OC
是底边AB上的中线
∴OC⊥AB
∴AB是⊙O的切线
B
A
E
D
C
O
例:如图: ⊙O的直径AB=4, ∠ABC=30°,BC=4 ,D是线段BC的中点。
(1)试判断点D与⊙O的位置关系
(2)过点D作DE⊥AC,垂足为点E,求证:直线DE是⊙O的切线
3
A
B
l
O
圆O与直线l相切,则过点A的直径A B与切线l有
怎样的位置关系?
垂直
.
O
A
L
将上页思考中的问题
反过来,如果L是⊙O
的切线,切点为A,那么
半径OA与直线L是不
是一定垂直呢
一定垂直
切线的性质定理:
圆的切线垂直于过切点的半径
A
B
C
D
O
例:如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,求证:AC平分∠DAB
A
B
O
D
C
例:已知:AB是⊙O的直径,BC是⊙O切线,切点为B,OC平行于弦AD,求证:DC是⊙O的切线。
探 究 活 动
如图,纸上有一⊙O ,PA为⊙O的一条切线,沿着直线PO对折,设圆上与点A重合的点为B。
1、OB是⊙O的一条半径吗?
2、PB是⊙O的切线吗?
5、利用图形轴对称性解释
3、PA、PB有何关系?
4、∠APO和∠ BPO有何关系?
A
O
P
P
A
O
B
经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长。
如图,P是⊙O外一点,PA,PB是⊙O的两条切线,我们把线段PA,PB的长叫做点P到⊙O的切线长。
O
P
A
B
切线和切线长是两个不同的概念,
切线是直线,不能度量;
切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量。
O
P
A
B
O
P
A
B
∟
∟
M
根据你的直观判断,猜想图中PA是否等于PB?∠1与∠2又有什么关系?
大胆猜想:
⌒
⌒
1
2
证明:
∵PA、PB是⊙o的两条切线,
∴OA⊥AP,OB⊥BP
又OA=OB,OP=OP,
∴Rt△AOP≌Rt△BOP(HL)∴PA=PB,∠1=∠2
关键是作辅助线~
切线长定理:
从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
O
P
A
B
已知:⊙O的半径为3厘米,点P和圆心O的距离为6厘米,经过点P和⊙O的两条切线,求这两条切线的夹角及切线长.
练习一
O
F
P
E
⌒
1
2
⌒
切线长定理的拓展
B
O
P
A
H
D
C
想一想:根据图形,
你还可以得到什么结论?
平分切点所成的两弧;垂直平分切点所成的弦.
P
A
B
C
O
如AC为直径,观察OP与BC的位置关系,并给予证明。
巩固练习:
(1)已知OA=3cm,OP=6cm,则PA=——,∠APB=——
3√3
60°
(2)OP交⊙O于M,则——————,AB与OP有何关系?
AM=BM
⌒
⌒
M
已知:如图,PA、PB是⊙O的切线,切点分别是A、B,Q为AB上一点,过Q点作⊙O的切线,交PA、PB于E、F点,已知PA=12CM,∠P=70
求:△PEF的周长。
E
A
Q
P
F
B
O
思考
如图,一张三角形的铁皮,如何在它上面截下
一块圆形的用料,并且使圆的面积尽可能大呢
I
D
内切圆和内心的定义:
与三角形各边都相切的圆叫做三角形的内切圆.
内切圆的圆心是三角形三条角平分线的交点,叫
做三角形的内心.
例2 △ABC的内切圆⊙O与BC、CA、AB分别相切于
点D、E、F,且AB=9cm,BC=14cm,CA=13cm,
求AF、BD、CE的长.
解:
设AF=x(cm),则AE=x(cm)
∴CD=CE=AC-AE=13-x
BD=BF=AB-AF=9-x
由 BD+CD=BC可得
(13-x)+(9-x)=14
解得 x=4
∴ AF=4(cm), BD=5(cm), CE=9(cm).
练 习 1
如图,△ABC中,∠ ABC=50°,∠ACB=75 °,点O
是⊙O的内心,求∠ BOC的度数。
A
O
C
B
解:∵点O是⊙O的内心
∴∠OBC=1/2∠ABC=25°
∠OCB=1/2∠ACB=37.5°
∴ ∠BOC=180°﹣25°﹣37.5°
=117.5°
练 习 2
△ABC的内切圆半径为 r , △ABC的周长为 l ,求△ABC
的面积。 (提示:设内心为O,连接OA、OB、OC。)
O
A
C
B
r
解:连接OA、OB、OC,则
S= AB × r + AC × r + BC × r
= (AB +AC+BC) × r
= l r
r
r
r
记忆:
1. Rt△ABC中,∠C=90°,a=3,b=4,则内切圆的半径是_______.
1
练习1.在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,以D为
圆心,DB长为半径作⊙D.试说明:AC是⊙D的切线.
F
2.AB是⊙O的弦,C是⊙O外一点,BC是⊙O的切线,AB交
过C点的直径于点D,OA⊥CD,试判断△BCD的形状,并
说明你的理由.
3.AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过点E
作⊙O的切线交AC于点D,试判断△AED的形状,并
说明理由.
基础题:
1.既有外接圆,又内切圆的平行四边形是______.
2.直角三角形的外接圆半径为5cm,内切圆半径为1cm,
则此三角形的周长是_______.
3.⊙O边长为2cm的正方形ABCD的内切圆,E、F切⊙O
于P点,交AB、BC于E、F,则△BEF的周长是_____.
E
F
H
G
正方形
22cm
2cm
4.已知:三角形ABC内接于⊙O,过点A作直线EF.
(1)图甲,AB为直径,要使得EF是⊙O切线,还需添加的条件
(只需写出三种情况)①___________②_____________
③______________.
(2)图乙, AB为非直径的弦,∠CAE=∠B.求证:EF是⊙O的
切线.
∠CAE=∠B
AB⊥FE
∠BAC+∠CAE=90°
H
5.小红家的锅盖坏了,为了配一个锅盖,需要测量锅盖的
直径(锅边所形成的圆的直径),而小红家只有一把长20cm
的直尺,根本不够长,怎么办呢 小红想了想,采取以下方
法:首先把锅平放到墙根,锅边刚好靠到两墙,用直尺紧贴
墙面量得MA的长,即可求出墙的直径,请你利用图乙,说
明她这样做的道理.
6.已知直角梯形 ABCD 中,AD∥BC,AB⊥BC,以腰DC的中点 E 为圆心的圆与 AB 相切,梯形的上底 AD 与底 BC 是方程 x 2-10x + 16 = 0 的两根,求 ⊙E 的半径 r .
F
同课章节目录
