等腰三角形的性质
图片预览





文档简介
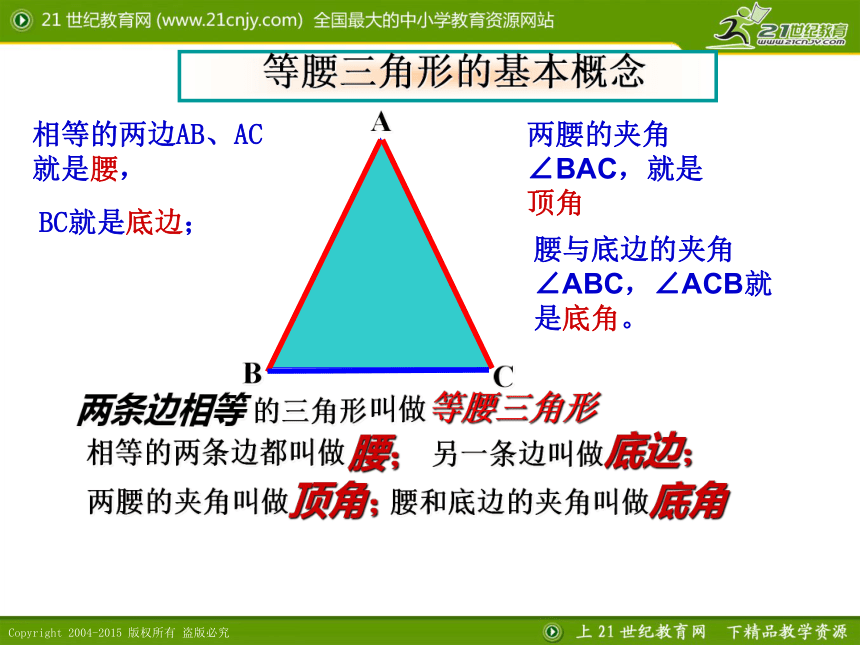
课件14张PPT。13.3.1 等腰三角形有关概念和性质第十三章 全等三角形 等腰三角形的基本概念两条边相等的三角形叫做等腰三角形相等的两条边都叫做腰;另一条边叫做底边;两腰的夹角叫做顶角;腰和底边的夹角叫做底角相等的两边AB、AC就是腰,BC就是底边;两腰的夹角∠BAC,就是顶角腰与底边的夹角∠ABC,∠ACB就是底角。现在请同学们做一张等腰三角形的半透明纸片,
每个人的等腰三角形的大小和形状可以不一样,
把纸片对折,让两腰 AB、AC重叠在一起,折痕
为AD,你能发现什么现象呢?
请大家尽可能多地写出结论!实验:结论:1、等腰三角形是轴对称图形2、∠ B =∠ C3、BD = CD ,AD 为底边上的中线4、∠ADB = ∠ADC = 90°,AD为底边上的高5、∠BAD = ∠CAD ,AD为顶角平分线问题1、结论(2)用文字如何表述?等腰三角形的两个底角相等(简写“等边对等角”)问题2、结论(3)、(4)、(5)用一句话可以归纳为什么语句?等腰三角形的顶角平分线、底边上的中线
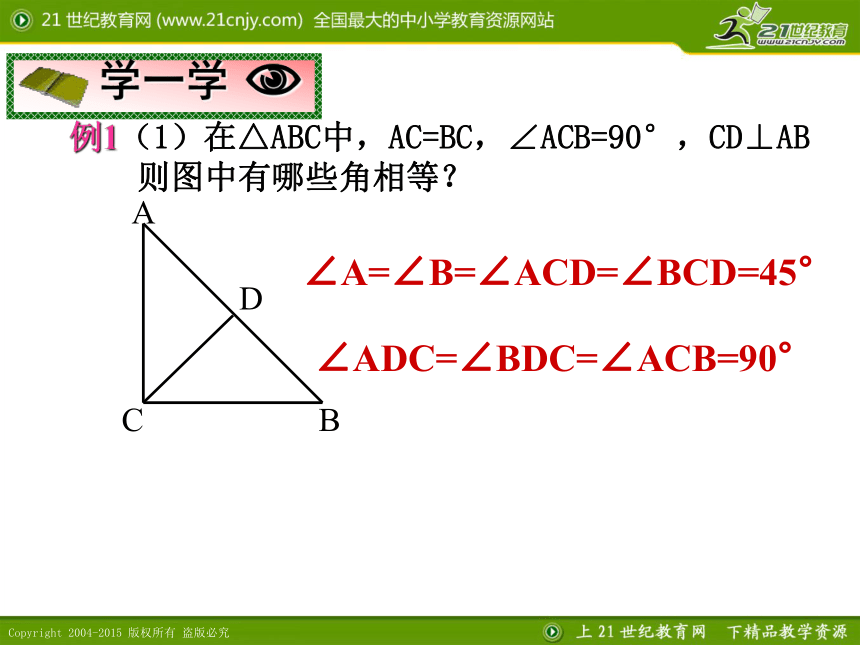
和底边上的高互相重合,简称“三线合一”归纳: 75°, 30°70°,40°或55°,55°35°,35° 例1(1)在△ABC中,AC=BC,∠ACB=90°,CD⊥AB
则图中有哪些角相等?∠A=∠B=∠ACD=∠BCD=45°∠ADC=∠BDC=∠ACB=90°例2:已知:如图,房屋的顶角∠BAC=100°,过屋顶A的立柱AD⊥BC,屋椽AB=AC, 求顶架上∠B、∠C、∠BAD、∠CAD的度数。解:在△ABC中,∵AB=AC(已知)∴∠B=∠C(等边对等角)∴∠B=∠C= =40°又∵AD⊥BC(已知)∴∠BAD=∠CAD(等腰三角形顶角的
平分线与底边上的高互相重合)∴∠BAD=∠CAD=50°学一学?答:……在等腰三角形中,有一种特殊的情况,就是
底边与腰相等,这时,三角形三边相等。 我们把三条边都相等的三角形叫做等边三角形(正三角形)。问题1: 等边三角形具有什么性质?(1)等边三角形的各角都相等,并且每一个
角都等于60°;问题2:等边三角形是轴对称图形吗?
如果是,有几条对称轴?(2)是,有三条对称轴。例3、如图,在△ABC中,AB = AC,D是BC边上的中点,
∠B = 30°,求 ∠1 和 ∠ADC的度数。解:∵AB = AC,AD是BC边上的中线∴ ∠1 = ∠ 2∴ ∠ADC = 90°∵ ∠ BAC =180° - 30°-30° = 120° ∴∵ AB = AC∴ AD是BC边上的高,同时也是
顶角∠BAC的平分线。(三线合一)∴ ∠C =∠B=30°1、判断下列命题是否正确。(1)等腰三角形的角平分线、中线和高互相重合( )
(2)有一个角是60°的等腰三角形,其它两个内角也为60°( )
(3)等腰三角形的一条高把它分成两个完全一样
的直角三角形 ( )
(4)等腰三角形内的一点与底边的两个端点的距离相等
则这个点在底边的高上。 ( )练一练×√×√解:∵AB = AC,AD是∠BAC的平分线∴ ∠1 =∠ 2= 25°∴ ∠ADB =90° 答:∠ADB =90°,∠B=65°在Rt△ABD中,
∵∠B+∠1=90°∴ AD是BC边上的高(三线合一)∴ ∠B=90°-25°=65°2、如图,在△ABC中,已知 AB = AC ,AD为∠BAC的平分线,且∠2=25°,求∠ADB和∠B的度数。小结:1、等腰三角形的性质:等边对等角2、等腰三角形的顶角平分线、底边上的中线
和底边上的高互相重合(三线合一)3、由等腰三角形的性质推出等边三角形的
各角都相等,且都等于60°。 4、“三线合一”性质在实际应用中,只要有其中一个结论成立,其它两个结论一下成立,所以关键是寻找其中一个结论成立的条件。 作业
每个人的等腰三角形的大小和形状可以不一样,
把纸片对折,让两腰 AB、AC重叠在一起,折痕
为AD,你能发现什么现象呢?
请大家尽可能多地写出结论!实验:结论:1、等腰三角形是轴对称图形2、∠ B =∠ C3、BD = CD ,AD 为底边上的中线4、∠ADB = ∠ADC = 90°,AD为底边上的高5、∠BAD = ∠CAD ,AD为顶角平分线问题1、结论(2)用文字如何表述?等腰三角形的两个底角相等(简写“等边对等角”)问题2、结论(3)、(4)、(5)用一句话可以归纳为什么语句?等腰三角形的顶角平分线、底边上的中线
和底边上的高互相重合,简称“三线合一”归纳: 75°, 30°70°,40°或55°,55°35°,35° 例1(1)在△ABC中,AC=BC,∠ACB=90°,CD⊥AB
则图中有哪些角相等?∠A=∠B=∠ACD=∠BCD=45°∠ADC=∠BDC=∠ACB=90°例2:已知:如图,房屋的顶角∠BAC=100°,过屋顶A的立柱AD⊥BC,屋椽AB=AC, 求顶架上∠B、∠C、∠BAD、∠CAD的度数。解:在△ABC中,∵AB=AC(已知)∴∠B=∠C(等边对等角)∴∠B=∠C= =40°又∵AD⊥BC(已知)∴∠BAD=∠CAD(等腰三角形顶角的
平分线与底边上的高互相重合)∴∠BAD=∠CAD=50°学一学?答:……在等腰三角形中,有一种特殊的情况,就是
底边与腰相等,这时,三角形三边相等。 我们把三条边都相等的三角形叫做等边三角形(正三角形)。问题1: 等边三角形具有什么性质?(1)等边三角形的各角都相等,并且每一个
角都等于60°;问题2:等边三角形是轴对称图形吗?
如果是,有几条对称轴?(2)是,有三条对称轴。例3、如图,在△ABC中,AB = AC,D是BC边上的中点,
∠B = 30°,求 ∠1 和 ∠ADC的度数。解:∵AB = AC,AD是BC边上的中线∴ ∠1 = ∠ 2∴ ∠ADC = 90°∵ ∠ BAC =180° - 30°-30° = 120° ∴∵ AB = AC∴ AD是BC边上的高,同时也是
顶角∠BAC的平分线。(三线合一)∴ ∠C =∠B=30°1、判断下列命题是否正确。(1)等腰三角形的角平分线、中线和高互相重合( )
(2)有一个角是60°的等腰三角形,其它两个内角也为60°( )
(3)等腰三角形的一条高把它分成两个完全一样
的直角三角形 ( )
(4)等腰三角形内的一点与底边的两个端点的距离相等
则这个点在底边的高上。 ( )练一练×√×√解:∵AB = AC,AD是∠BAC的平分线∴ ∠1 =∠ 2= 25°∴ ∠ADB =90° 答:∠ADB =90°,∠B=65°在Rt△ABD中,
∵∠B+∠1=90°∴ AD是BC边上的高(三线合一)∴ ∠B=90°-25°=65°2、如图,在△ABC中,已知 AB = AC ,AD为∠BAC的平分线,且∠2=25°,求∠ADB和∠B的度数。小结:1、等腰三角形的性质:等边对等角2、等腰三角形的顶角平分线、底边上的中线
和底边上的高互相重合(三线合一)3、由等腰三角形的性质推出等边三角形的
各角都相等,且都等于60°。 4、“三线合一”性质在实际应用中,只要有其中一个结论成立,其它两个结论一下成立,所以关键是寻找其中一个结论成立的条件。 作业
