13.2.5 全等三角形的判定(SSS)课件
文档属性
| 名称 | 13.2.5 全等三角形的判定(SSS)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 373.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-11-06 07:20:01 | ||
图片预览



文档简介
课件12张PPT。 全等三角形的判定 13.2.5边边边 情景导入:有一块三角形板材 要∠MAN平分开,现在只有一把直尺和一根细绳,怎么办,说明理由有一块三角形板材 要把∠MAN平分开,现在只有一把直尺和一根细绳,怎么办,说明理由?一、学习目标1、理解和掌握 “S.S.S”判定方法;能运用其判定两个三角形全等.
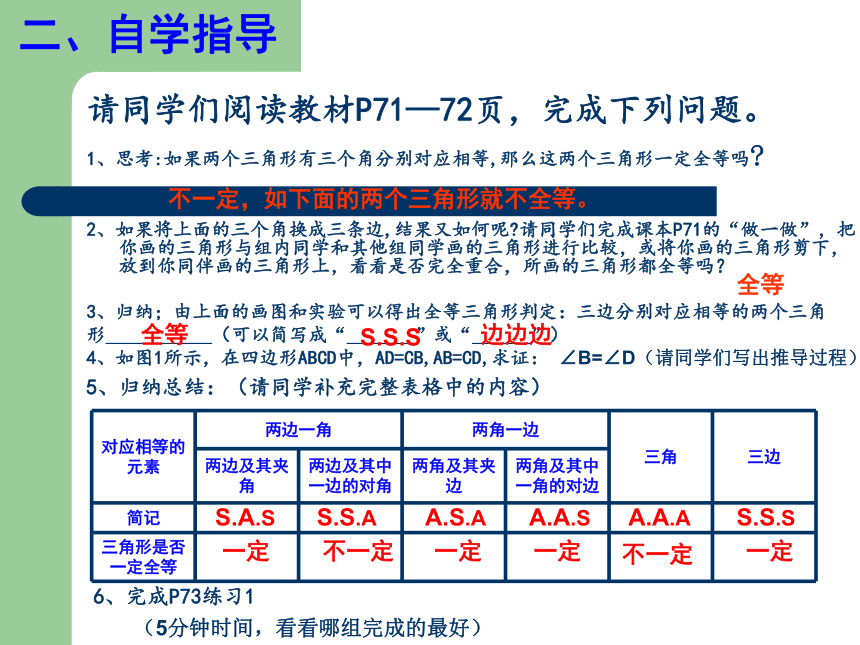
能运用“S.S.S”判定方法来证明角和线段相等二、自学指导1、思考:如果两个三角形有三个角分别对应相等,那么这两个三角形一定全等吗?
2、如果将上面的三个角换成三条边,结果又如何呢?请同学们完成课本P71的“做一做”,把你画的三角形与组内同学和其他组同学画的三角形进行比较,或将你画的三角形剪下,放到你同伴画的三角形上,看看是否完全重合,所画的三角形都全等吗?
3、归纳;由上面的画图和实验可以得出全等三角形判定:三边分别对应相等的两个三角
形 (可以简写成“ ”或“ ”)
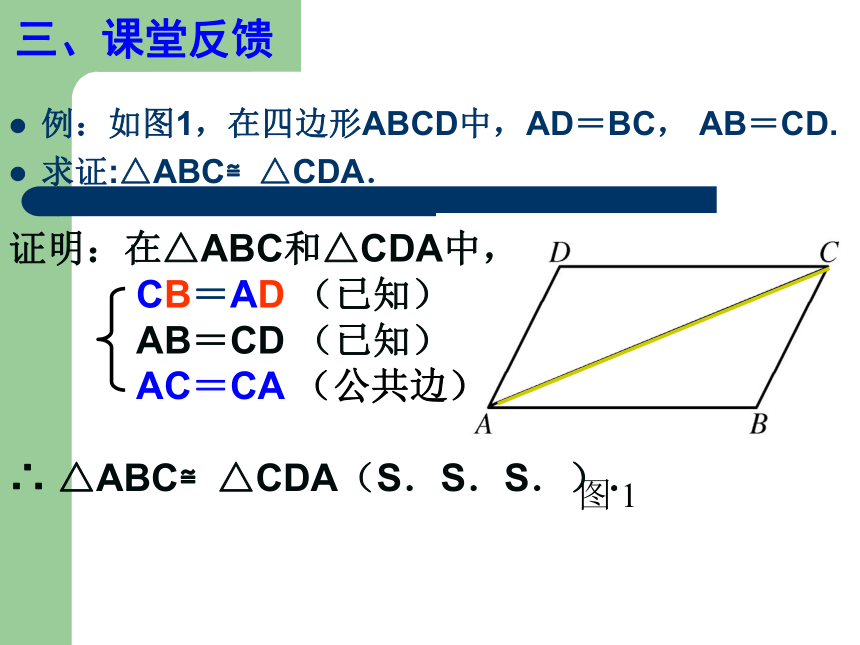
4、如图1所示,在四边形ABCD中,AD=CB,AB=CD,求证: ∠B=∠D(请同学们写出推导过程)请同学们阅读教材P71—72页,完成下列问题。不一定,如下面的两个三角形就不全等。5、归纳总结:(请同学补充完整表格中的内容)S.A.SA.A.SA.S.AS.S.AA.A.AS.S.S一定一定一定不一定不一定一定6、完成P73练习1全等(5分钟时间,看看哪组完成的最好)例:如图1,在四边形ABCD中,AD=BC, AB=CD.
求证:△ABC≌△CDA.
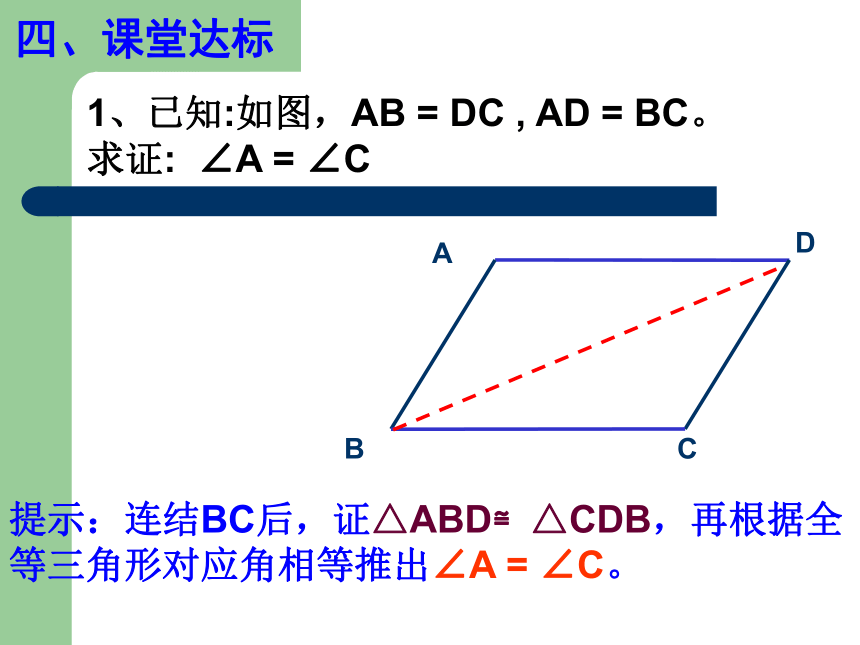
三、课堂反馈1、已知:如图,AB = DC , AD = BC。
求证: ∠A = ∠C提示:连结BC后,证△ABD≌△CDB,再根据全等三角形对应角相等推出∠A = ∠C。四、课堂达标2、已知:如图.AB = DC , AC = DB
求证: ∠A = ∠D提示:BC为公共边,由SSS可得两三角形全等,全等三角形对应角相等。
3、已知:如图.AB = AD ,BC = DC
求证:∠B= ∠D证明:连结AC在△ABC与△ADC中∴ △ABC≌△ADC (SSS)∴∠B=∠D(全等三角形对应角相等)(公共边)课堂小结 请说出目前有哪几种判定三角
形全等的方法?谈谈本节课的收获课后作业:课本P76页 习题13.2
1、第1、6题
2、课程导报第10期 13.2.5全等三角形的判定(sss)边边边公理: 三边 对应 相等的两个三角形全等.(SSS)应用表达式:(如图)在△ABC与△DEF中∴ △ABC≌△DEF (SSS)
1. 根据条件分别判定下面的三角形是否全等.
(1) 线段AD与BC相交于点O,AO=DO, BO=CO. △ABO与△BCO;
(2) AC=AD, BC=BD. △ABC与△ABD;
(3) ∠A=∠C, ∠B=∠D. △ABO与△CDO;
(4) 线段AD与BC相交于点E,AE=BE, CE=DE, AC=BD. △ABC与△BAD?全等(SAS)全等(SSS)不能判定全等。全等(SSS等)
能运用“S.S.S”判定方法来证明角和线段相等二、自学指导1、思考:如果两个三角形有三个角分别对应相等,那么这两个三角形一定全等吗?
2、如果将上面的三个角换成三条边,结果又如何呢?请同学们完成课本P71的“做一做”,把你画的三角形与组内同学和其他组同学画的三角形进行比较,或将你画的三角形剪下,放到你同伴画的三角形上,看看是否完全重合,所画的三角形都全等吗?
3、归纳;由上面的画图和实验可以得出全等三角形判定:三边分别对应相等的两个三角
形 (可以简写成“ ”或“ ”)
4、如图1所示,在四边形ABCD中,AD=CB,AB=CD,求证: ∠B=∠D(请同学们写出推导过程)请同学们阅读教材P71—72页,完成下列问题。不一定,如下面的两个三角形就不全等。5、归纳总结:(请同学补充完整表格中的内容)S.A.SA.A.SA.S.AS.S.AA.A.AS.S.S一定一定一定不一定不一定一定6、完成P73练习1全等(5分钟时间,看看哪组完成的最好)例:如图1,在四边形ABCD中,AD=BC, AB=CD.
求证:△ABC≌△CDA.
三、课堂反馈1、已知:如图,AB = DC , AD = BC。
求证: ∠A = ∠C提示:连结BC后,证△ABD≌△CDB,再根据全等三角形对应角相等推出∠A = ∠C。四、课堂达标2、已知:如图.AB = DC , AC = DB
求证: ∠A = ∠D提示:BC为公共边,由SSS可得两三角形全等,全等三角形对应角相等。
3、已知:如图.AB = AD ,BC = DC
求证:∠B= ∠D证明:连结AC在△ABC与△ADC中∴ △ABC≌△ADC (SSS)∴∠B=∠D(全等三角形对应角相等)(公共边)课堂小结 请说出目前有哪几种判定三角
形全等的方法?谈谈本节课的收获课后作业:课本P76页 习题13.2
1、第1、6题
2、课程导报第10期 13.2.5全等三角形的判定(sss)边边边公理: 三边 对应 相等的两个三角形全等.(SSS)应用表达式:(如图)在△ABC与△DEF中∴ △ABC≌△DEF (SSS)
1. 根据条件分别判定下面的三角形是否全等.
(1) 线段AD与BC相交于点O,AO=DO, BO=CO. △ABO与△BCO;
(2) AC=AD, BC=BD. △ABC与△ABD;
(3) ∠A=∠C, ∠B=∠D. △ABO与△CDO;
(4) 线段AD与BC相交于点E,AE=BE, CE=DE, AC=BD. △ABC与△BAD?全等(SAS)全等(SSS)不能判定全等。全等(SSS等)
