数学人教A版(2019)必修第一册5.5.1 两角差的余弦公式(共20张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册5.5.1 两角差的余弦公式(共20张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-12 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
人教版高中数学必修第册(A版)
第五章 三角函数
5.5.1 两角差的余弦公式
创设情境 提出问题
皇冠大扶梯,位于重庆,是亚洲第二长的一级提升坡地大扶梯。该扶梯全长米,宽1.3米,提升高度52.7米,倾斜度为30度。请问电梯水平方向前进了多少米?
解:设电梯水平方向前进了则
创设情境 提出问题
问题1:扶梯的全长不变,若扶梯倾斜度为,此时水平方向又前进了多少米?
解:设电梯水平方向前进了则
探究公式 大胆猜想
问题多少?能否用特殊三角函数值来表示?
问题 ?
等式不成立
问题,能够?
探究公式 大胆猜想
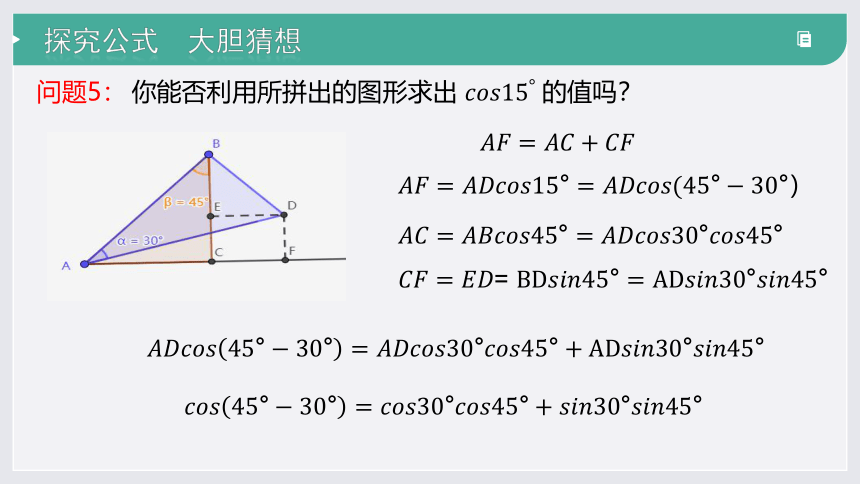
问题5: 你能否利用所拼出的图形求出 的值吗?
=
探究公式 大胆猜想
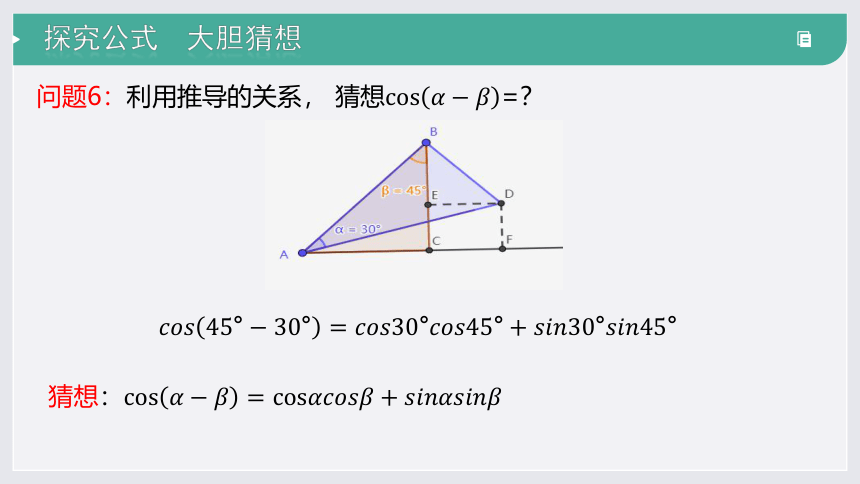
猜想
问题6:利用推导的关系, =?
公式证明 剖析公式
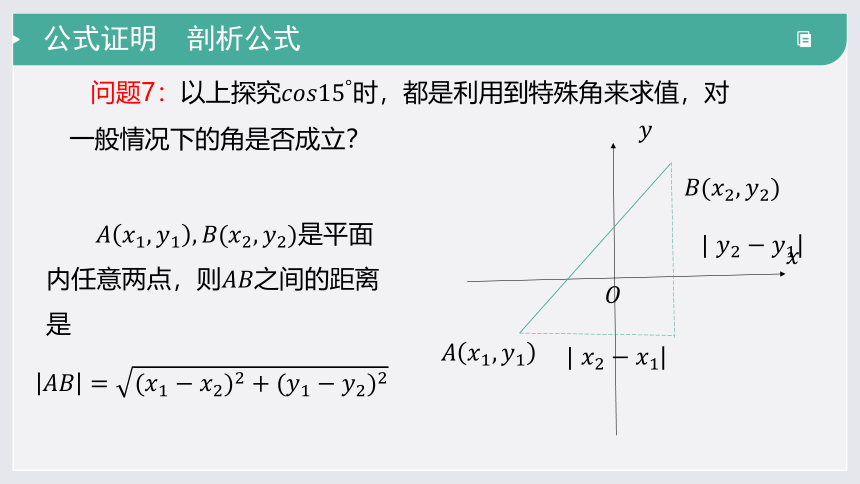
是平面内任意两点,则之间的距离是
|
|
问题7:以上探究时,都是利用到特殊角来求值,对一般情况下的角是否成立?
公式证明 剖析公式
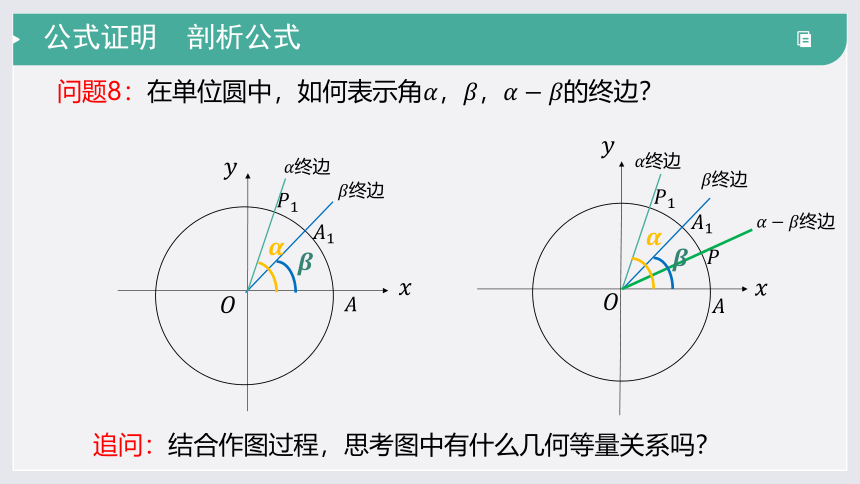
追问作图过程,思考图中有什么几何等量关系吗?
终边
终边
终边
终边
终边
问题8:在单位圆中,如何表示角的终边?
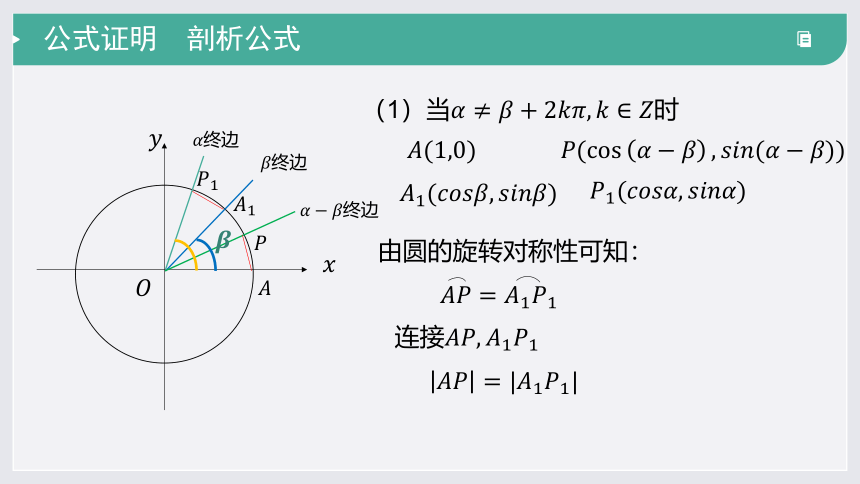
公式证明 剖析公式
(1)当时
由圆的旋转对称性可知:
连接
终边
终边
终边
公式证明 剖析公式
化简得:
由两点间的距离公式得:
终边
终边
终边
公式证明 剖析公式
问题9:等式还成立吗?
(1)当时
(2)当时
称为两角差的余弦公式,简记为:
公式证明 剖析公式
对于任意角都有
口诀:CCSS,符号相反
问题10:对于任意角都有成立?
公式史料 了解文化
19世纪法国数学家萨吕斯提出坐标法,1941年,美国数学家麦克肖恩在此基础上进行改进,应用全等以及两点间的距离公式进行推导,称为单位圆法模型,如图1。
图 1
拓展思考 三角形面积推导两角差的余弦公式
中国科学院张景中先生从上世纪80年代就开始研究用面积法解决几何证明问题,进而形成了几何学中的新体系,并创造了几何定理机器证明的“消点法.
课后思考:我们能够通过如上图来推导两角差的余弦公式吗?
公式应用 巩固新知
例1.若扶梯倾斜度为,此时水平方向又前进了多少米?
解:设电梯水平方向前进了则
证明:
公式应用 巩固新知
例2.利用公式证明:
(1) (2)
(1)
证明:
公式应用 巩固新知
例2.利用公式证明:
(1) (2)
(2)
梳理总结 深化思维
模型思想
推理思想
抽象思想
数形结合思想
生活实例
圆的旋转对称性
两点间的距离公式
作业布置 发展素养
2.思考题
(1)运用课堂上所提的面积法及图形,推导两角差的余弦公式;
(2)通过查阅相关资料,自主研究公式的其他推导方法.
1.课本P217练习1,3,4
(3)仿照本节课的研究思路,并结合已学知识进行探究性证明,你还能得到其他等式吗?
恳请老师和各位同学批评指正
人教版高中数学必修第册(A版)
第五章 三角函数
5.5.1 两角差的余弦公式
创设情境 提出问题
皇冠大扶梯,位于重庆,是亚洲第二长的一级提升坡地大扶梯。该扶梯全长米,宽1.3米,提升高度52.7米,倾斜度为30度。请问电梯水平方向前进了多少米?
解:设电梯水平方向前进了则
创设情境 提出问题
问题1:扶梯的全长不变,若扶梯倾斜度为,此时水平方向又前进了多少米?
解:设电梯水平方向前进了则
探究公式 大胆猜想
问题多少?能否用特殊三角函数值来表示?
问题 ?
等式不成立
问题,能够?
探究公式 大胆猜想
问题5: 你能否利用所拼出的图形求出 的值吗?
=
探究公式 大胆猜想
猜想
问题6:利用推导的关系, =?
公式证明 剖析公式
是平面内任意两点,则之间的距离是
|
|
问题7:以上探究时,都是利用到特殊角来求值,对一般情况下的角是否成立?
公式证明 剖析公式
追问作图过程,思考图中有什么几何等量关系吗?
终边
终边
终边
终边
终边
问题8:在单位圆中,如何表示角的终边?
公式证明 剖析公式
(1)当时
由圆的旋转对称性可知:
连接
终边
终边
终边
公式证明 剖析公式
化简得:
由两点间的距离公式得:
终边
终边
终边
公式证明 剖析公式
问题9:等式还成立吗?
(1)当时
(2)当时
称为两角差的余弦公式,简记为:
公式证明 剖析公式
对于任意角都有
口诀:CCSS,符号相反
问题10:对于任意角都有成立?
公式史料 了解文化
19世纪法国数学家萨吕斯提出坐标法,1941年,美国数学家麦克肖恩在此基础上进行改进,应用全等以及两点间的距离公式进行推导,称为单位圆法模型,如图1。
图 1
拓展思考 三角形面积推导两角差的余弦公式
中国科学院张景中先生从上世纪80年代就开始研究用面积法解决几何证明问题,进而形成了几何学中的新体系,并创造了几何定理机器证明的“消点法.
课后思考:我们能够通过如上图来推导两角差的余弦公式吗?
公式应用 巩固新知
例1.若扶梯倾斜度为,此时水平方向又前进了多少米?
解:设电梯水平方向前进了则
证明:
公式应用 巩固新知
例2.利用公式证明:
(1) (2)
(1)
证明:
公式应用 巩固新知
例2.利用公式证明:
(1) (2)
(2)
梳理总结 深化思维
模型思想
推理思想
抽象思想
数形结合思想
生活实例
圆的旋转对称性
两点间的距离公式
作业布置 发展素养
2.思考题
(1)运用课堂上所提的面积法及图形,推导两角差的余弦公式;
(2)通过查阅相关资料,自主研究公式的其他推导方法.
1.课本P217练习1,3,4
(3)仿照本节课的研究思路,并结合已学知识进行探究性证明,你还能得到其他等式吗?
恳请老师和各位同学批评指正
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
