8.3 再探索实际问题与二元一次方程组(3)[下学期]
文档属性
| 名称 | 8.3 再探索实际问题与二元一次方程组(3)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 440.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-04-10 00:00:00 | ||
图片预览






文档简介
课件23张PPT。8.3 再探索实际问题与二元一次方程组(3)第八章二元一次方程组 最近几年,全国各地普遍出现了夏季用电紧张的局面,为疏导电价矛盾,促进居民节约用电、合理用电,各地出台了峰谷电价试点方案。
电力行业中峰谷的含义是用山峰和山谷来形象比喻功率负荷特性的变化幅度。一般白天的用电比较集中、用电功率大,而夜里人们休息时用电比较小,所以通常白天的用电称为是高峰用电,即8:00—22:00,深夜的用电是低谷用电即22:00—次日8:00。
若某地的高峰电价为每千瓦时0.56元;低谷电价为每千瓦时0.28元。八月份小明家的总用电量为125千瓦时,总电费为49元,你知道他家高峰用电量和低谷用电量各是多少千瓦时吗?设他家高峰用电量x千瓦时和低谷用电量y千瓦时
相等关系:
高峰用电量+低谷用电量=总用电量(千瓦时)
几个数量: 高峰电价为每千瓦时0.56元; 低谷电价为每千瓦时0.28元。 小明家总用电量为125千瓦时,总电费为49元x + y = 125高峰电费+低谷电费=总电费(元)0.56x + 0.28y = 49解:设小明家高峰用电量为x千瓦时,低谷用电量为y千瓦时,则 x + y = 125 ①
0.56x + 0.28y = 49 ②
{x = 50
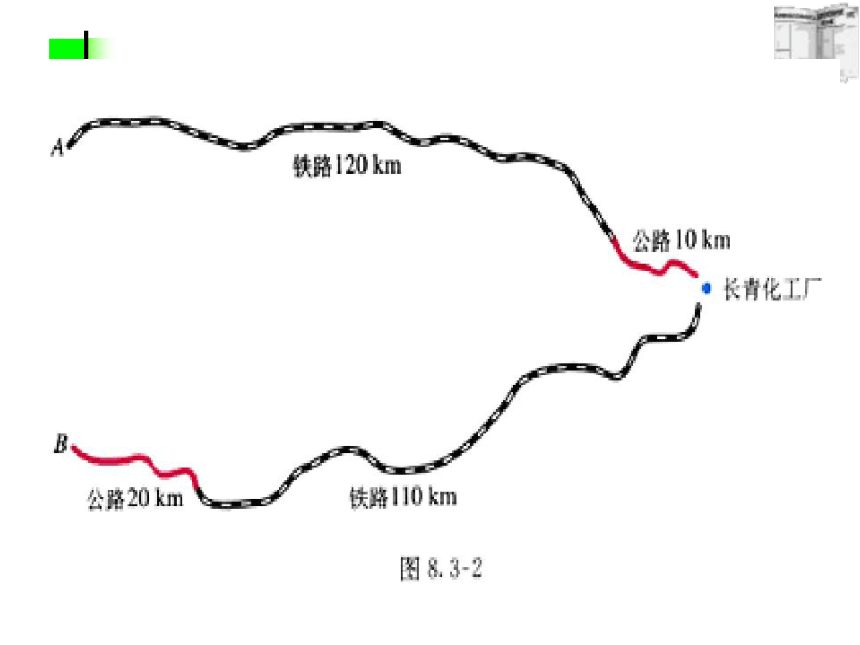
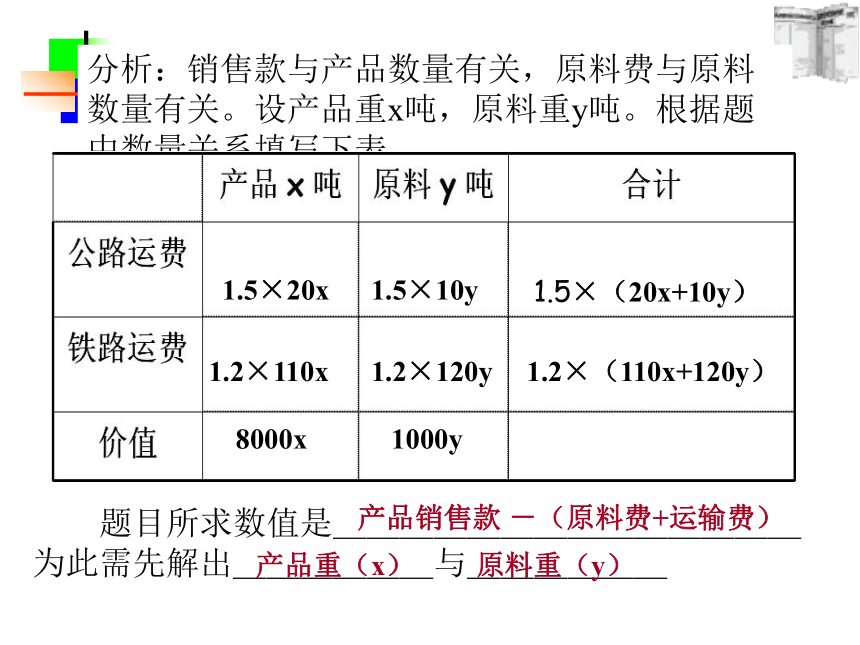
y = 75解得答:小明家高峰用电量为50千瓦时,低谷用电量为75千瓦时。你忘记检验了吧!{探究3 如图8.3-2,长青化工厂与A,B两地有公路、铁路相连。这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地。公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元。这批产品的销售款比原料费与运输费的和多多少元?分析:销售款与产品数量有关,原料费与原料数量有关。设产品重x吨,原料重y吨。根据题中数量关系填写下表。1.5×20x1.5×10y1.5×(20x+10y)1.2×110x1.2×120y1.2×(110x+120y)8000x1000y 题目所求数值是______________
为此需先解出______与______
产品销售款 -(原料费+运输费)产品重(x)原料重(y)____________
____________由上表,列方程组{1.5×(20x+10y)=150001.2×(110x+120y)=97200解这个方程组,得x = ___
y = ___300400 因此,这批产品的销售款比原料费与运输费的和多___ 元1887800 {解:设产品重x吨,原料重y吨,则{1.5×(20x+10y)=150001.2×(110x+120y)=97200解这个方程组,得x = 300
y = 400 8000x -(1000y+15000+97200)
=8000 × 300-(1000×400+15000+97200)
=1887800(元)答:这批产品的销售款比原料费与运输费的和1887800元。{ 从以上探究可以看出,方程组是解决含有多个未知数问题的重要工具。列出方程组要根据问题中的数量关系,解出方程组的解后,应进一步考虑它是否符合问题的实际意义。练习1:一批蔬菜要运往某批发市场,菜农准备用汽车公司的甲乙两种货车,已知过去两次租用这两种货车的记录如下表所示。 这批蔬菜需租用5辆甲种货车、2辆乙种货车刚好一次运完,如果每吨付20元运费
问:菜农应付运费多少元?答:要刚好一次运完,菜农应付运费500元。 练习2:为引导公民节约用水,合理利用资源,各地采用了价格调控手段。某地规定如下用收费标准:每户每月的用水不超过10吨,每吨按a元收费;超过10吨,超过的部分每吨按b元收费。小明家7、8两月份的用水记录如下:根据以上信息,你能求出a、b的值吗?解:依题意得 10a +(12 - 10)b = 15 ① 10a +(16 - 10)b = 21 ②解得
a = 1.2
b = 1.5答:a = 1.2 ,b = 1.5注:题目中已有a、b,不必再设{{你会了吗?某学校现有学生数1290人,与去年相比,男生增加20%,女生减少10%,学生总数增加7.5%,问现在学校中男生、女生各是多少? 友情提示:
可要想清楚了,到底设的是什么?解得
x=840
y=450解法一:设现在学校中男生有x人、女生有 y人,则x+y=1290
x y 1290
1+20% 1 –10% 1+7.5%
—————— + —————— = ——————{答:现在学校中男生有840人、女生有450人。{ (1+20% )x+( 1 –10% )y = 1290
1290
1+7.5%
解法二:设去年学校中男生有x人、女生有 y人,则 x + y = ————解得
x=700
y=500(1+20% )x=840,( 1 –10% )y=450答:现在学校中男生有840人、女生有450人。{{ 请试一试:某瓜果基地生产一种特色水果,若在市场上直接销售,每吨利润为1000元;经粗加工后销售,每吨利润增为4500元;经精加工后销售,每吨利润可达7500元。一食品公司收购到这种水果140吨,准备加工后上市销售。该公司的加工能力是:每天可以精加工6吨或者粗加工16吨,但两种加工方式不能同时进行。受季节等条件限制,公司必须在15天内将这批水果全部销售或加工完毕,为此公司研制了三种可行的方案:
方案一:将这批水果全部进行粗加工
方案二:尽可能多对水果进行精加工,没来得及加工的水果在市场上销售;
方案三:将部分水果进行精加工,其余进行粗加工,并恰好15天完成。
你认为选择那种方案获利最多?为什么? 按方案三所获得的利润为:
设共精加工了x吨,粗加工了y吨,于是有
x+ y =140 ① 解得 x=60
x y y=80
6 16
则方案三所获得的利润为
60 ×7500 + 80 ×4500 = 810000(元)
解:方案一获得的利润为:4500×140=630000(元) 方案二所获得的利润为:
6×15×7500+(140-6×15)×1000
= 725000(元){—— + —— = 15 ②{综上所述,按方案三所获得的利润最多。总结一下吧! 在用二元一次方程组解决实际问题时,你会怎样设定未知数,可借助那些方式辅助分析问题中的相等关系?作业:课本P116第5、6、9题(2004,黄冈)已知某电脑公司有A型、B型、C型三种型号的电脑,其价格分别为A型每台6000元,B型每台4000元,C型每台2500元。我市东坡中学计划将100500元钱全部用于从该电脑公司购进其中两种不同型号的电脑共36台,请你设计出几中不同的购买方案供该校选择,并说明理由。中考链接
电力行业中峰谷的含义是用山峰和山谷来形象比喻功率负荷特性的变化幅度。一般白天的用电比较集中、用电功率大,而夜里人们休息时用电比较小,所以通常白天的用电称为是高峰用电,即8:00—22:00,深夜的用电是低谷用电即22:00—次日8:00。
若某地的高峰电价为每千瓦时0.56元;低谷电价为每千瓦时0.28元。八月份小明家的总用电量为125千瓦时,总电费为49元,你知道他家高峰用电量和低谷用电量各是多少千瓦时吗?设他家高峰用电量x千瓦时和低谷用电量y千瓦时
相等关系:
高峰用电量+低谷用电量=总用电量(千瓦时)
几个数量: 高峰电价为每千瓦时0.56元; 低谷电价为每千瓦时0.28元。 小明家总用电量为125千瓦时,总电费为49元x + y = 125高峰电费+低谷电费=总电费(元)0.56x + 0.28y = 49解:设小明家高峰用电量为x千瓦时,低谷用电量为y千瓦时,则 x + y = 125 ①
0.56x + 0.28y = 49 ②
{x = 50
y = 75解得答:小明家高峰用电量为50千瓦时,低谷用电量为75千瓦时。你忘记检验了吧!{探究3 如图8.3-2,长青化工厂与A,B两地有公路、铁路相连。这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地。公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元。这批产品的销售款比原料费与运输费的和多多少元?分析:销售款与产品数量有关,原料费与原料数量有关。设产品重x吨,原料重y吨。根据题中数量关系填写下表。1.5×20x1.5×10y1.5×(20x+10y)1.2×110x1.2×120y1.2×(110x+120y)8000x1000y 题目所求数值是______________
为此需先解出______与______
产品销售款 -(原料费+运输费)产品重(x)原料重(y)____________
____________由上表,列方程组{1.5×(20x+10y)=150001.2×(110x+120y)=97200解这个方程组,得x = ___
y = ___300400 因此,这批产品的销售款比原料费与运输费的和多___ 元1887800 {解:设产品重x吨,原料重y吨,则{1.5×(20x+10y)=150001.2×(110x+120y)=97200解这个方程组,得x = 300
y = 400 8000x -(1000y+15000+97200)
=8000 × 300-(1000×400+15000+97200)
=1887800(元)答:这批产品的销售款比原料费与运输费的和1887800元。{ 从以上探究可以看出,方程组是解决含有多个未知数问题的重要工具。列出方程组要根据问题中的数量关系,解出方程组的解后,应进一步考虑它是否符合问题的实际意义。练习1:一批蔬菜要运往某批发市场,菜农准备用汽车公司的甲乙两种货车,已知过去两次租用这两种货车的记录如下表所示。 这批蔬菜需租用5辆甲种货车、2辆乙种货车刚好一次运完,如果每吨付20元运费
问:菜农应付运费多少元?答:要刚好一次运完,菜农应付运费500元。 练习2:为引导公民节约用水,合理利用资源,各地采用了价格调控手段。某地规定如下用收费标准:每户每月的用水不超过10吨,每吨按a元收费;超过10吨,超过的部分每吨按b元收费。小明家7、8两月份的用水记录如下:根据以上信息,你能求出a、b的值吗?解:依题意得 10a +(12 - 10)b = 15 ① 10a +(16 - 10)b = 21 ②解得
a = 1.2
b = 1.5答:a = 1.2 ,b = 1.5注:题目中已有a、b,不必再设{{你会了吗?某学校现有学生数1290人,与去年相比,男生增加20%,女生减少10%,学生总数增加7.5%,问现在学校中男生、女生各是多少? 友情提示:
可要想清楚了,到底设的是什么?解得
x=840
y=450解法一:设现在学校中男生有x人、女生有 y人,则x+y=1290
x y 1290
1+20% 1 –10% 1+7.5%
—————— + —————— = ——————{答:现在学校中男生有840人、女生有450人。{ (1+20% )x+( 1 –10% )y = 1290
1290
1+7.5%
解法二:设去年学校中男生有x人、女生有 y人,则 x + y = ————解得
x=700
y=500(1+20% )x=840,( 1 –10% )y=450答:现在学校中男生有840人、女生有450人。{{ 请试一试:某瓜果基地生产一种特色水果,若在市场上直接销售,每吨利润为1000元;经粗加工后销售,每吨利润增为4500元;经精加工后销售,每吨利润可达7500元。一食品公司收购到这种水果140吨,准备加工后上市销售。该公司的加工能力是:每天可以精加工6吨或者粗加工16吨,但两种加工方式不能同时进行。受季节等条件限制,公司必须在15天内将这批水果全部销售或加工完毕,为此公司研制了三种可行的方案:
方案一:将这批水果全部进行粗加工
方案二:尽可能多对水果进行精加工,没来得及加工的水果在市场上销售;
方案三:将部分水果进行精加工,其余进行粗加工,并恰好15天完成。
你认为选择那种方案获利最多?为什么? 按方案三所获得的利润为:
设共精加工了x吨,粗加工了y吨,于是有
x+ y =140 ① 解得 x=60
x y y=80
6 16
则方案三所获得的利润为
60 ×7500 + 80 ×4500 = 810000(元)
解:方案一获得的利润为:4500×140=630000(元) 方案二所获得的利润为:
6×15×7500+(140-6×15)×1000
= 725000(元){—— + —— = 15 ②{综上所述,按方案三所获得的利润最多。总结一下吧! 在用二元一次方程组解决实际问题时,你会怎样设定未知数,可借助那些方式辅助分析问题中的相等关系?作业:课本P116第5、6、9题(2004,黄冈)已知某电脑公司有A型、B型、C型三种型号的电脑,其价格分别为A型每台6000元,B型每台4000元,C型每台2500元。我市东坡中学计划将100500元钱全部用于从该电脑公司购进其中两种不同型号的电脑共36台,请你设计出几中不同的购买方案供该校选择,并说明理由。中考链接
