8.1二元一次方程组[下学期]
文档属性
| 名称 | 8.1二元一次方程组[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-04-20 07:55:00 | ||
图片预览







文档简介
课件22张PPT。很高兴,
今天我们在一起探究新的知识8、1二元一次方程组 你知道篮球比赛的规则吗?篮球联赛中,每场比赛都要分出胜负,每队胜一场得 2分,负一场得 1分。某队为了争取较好的名次,想在全部 22场比赛中得到40分,那么这个队胜负场数应分别是多少??解法一:设胜X场,则负(22-X)场。
根据题意得: 2X+(22-X)=40
解法二:设胜X场,负Y场。
根据题意得:X+Y=22 (1)
2X+Y=40 (2)
问题:
议一议观察:上述方程有什么共同的特点?x+y=222x+y=40含有两个未知数,并且未知数的指数
都是1的方程叫做①每个方程都含有两个未知数(X和y)②每个未知数的指数都是1定义:二元一次方程.问题:它与一元一次方程比较有什么不同呢?X+Y=22 (1)
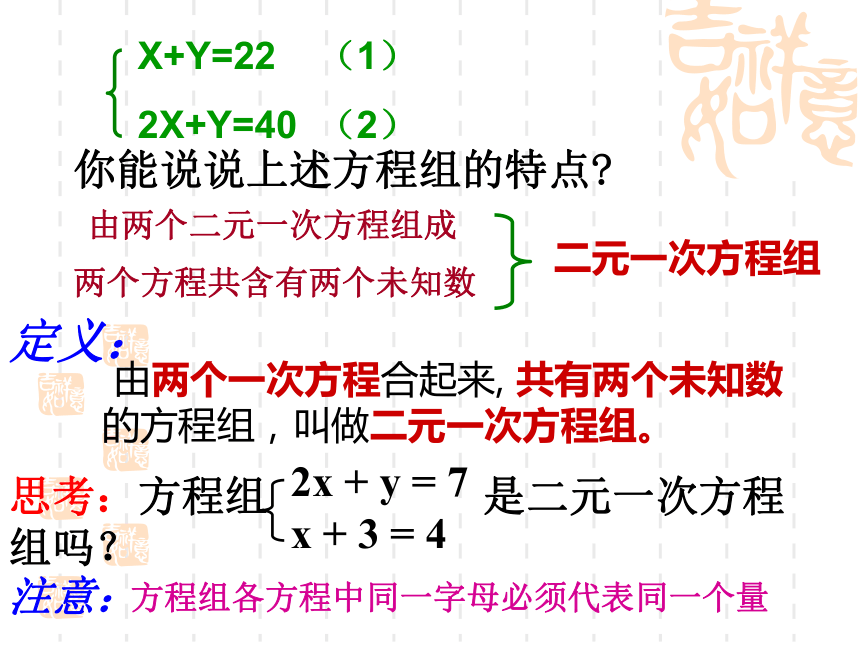
2X+Y=40 (2)你能说说上述方程组的特点?由两个二元一次方程组成 由两个一次方程合起来, 共有两个未知数的方程组,叫做二元一次方程组。方程组各方程中同一字母必须代表同一个量
二元一次方程组定义:注意:两个方程共含有两个未知数1、根据上面的定义请每位同学分别写一个
二元一次方程和二元一次方程组,并与
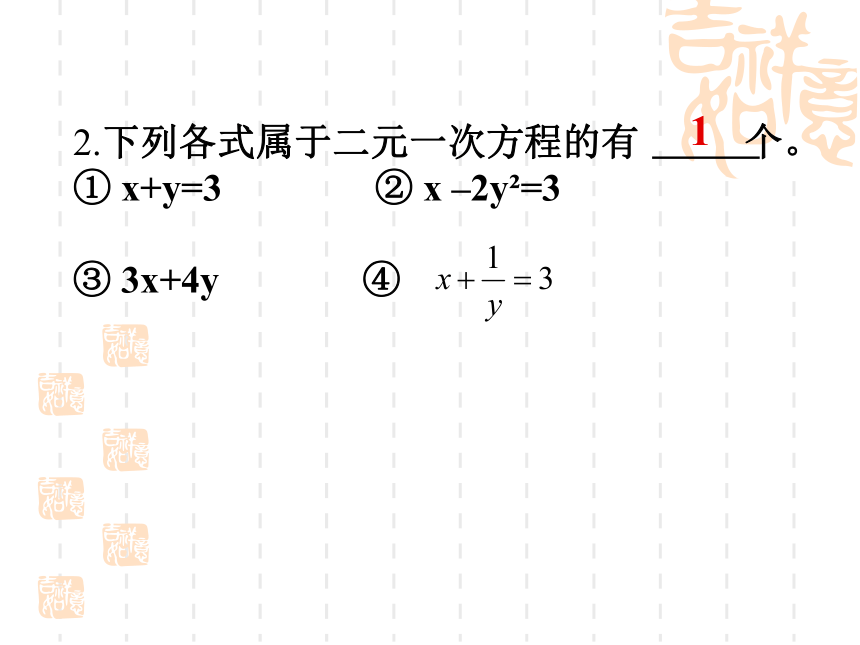
同桌交流。试一试2.下列各式属于二元一次方程的有 个。
① x+y=3 ② x –2y2=3
③ 3x+4y ④
13.下列方程组是二元一次方程组的是 ( )
3x=6 x+2y=5
5x =10 z=2x-5
x –2y=4 x –y=1
y=1 x2+y2=2 {{{ABDCC分析: x,y的指数必须是1次,此
方程才是二元一次方程
分别令n+1=1,3m –2=1,
n=0, m=1 4.若方程 是二元一次
方程,则n=________,m= ________0 1满足方程且符合实际意义? 探究022121222324567892112201011131314151617181943105678910111214151617181920使二元一次方程两边的值相等的两个未
知数的值,叫做二元一次方程的解。注意:二元一次方程的解有无数个。X=5
Y=17二元一次方程的解具有:不定性与相关性。有哪些X、Y的值满足方程且符合实际意义?探究022121222324567892112201011131314151617181943105678910111214151617181920上表中哪对x,y的值是方程的解?一般地,二元一次方程组的两个方程的公共解,
叫做二元一次方程组的解。X+Y=22 (1)
2X+Y=40 (2)的解是有哪些x,y的值例1:下列各对数值中是二元一次方程 的解的有
B: C: D:变式:其中是二元一次方程组的解是( )。A,B,CBA:例2、方程A:无数个;B:一个;C:三个;D:四个。在自然数范围内的解有( )试一试D 例3、小明家外出旅游,估计需要胶卷底片120张.商店里有两种型号的胶卷:A型每卷36张底片,B型每卷12张底片.小明一共买了4卷胶卷,刚好有120张底片.如果设两种胶卷分别买x卷和y卷,请根据问题中的条件列出关于x,y的方程学以致用:解:由题意,得1233211209672,并用列表尝试的方法求两种胶卷的数量.问题1:假设有一根11米长的绳子,要把它剪成两段,问每一段多少米?问题2:如果剪成的两段长度都是正整数米,怎样剪?问题3:如果要剪成的两段,长的一段比短的一段长3米,怎样剪?问题4:如果要剪成的三段长度都是正整数米,且这三段首尾顺次
相接组成一个三角形,怎样剪?x+y=11 这个二元一次方程有无穷多个解大展身手:今有鸡兔同笼,
上有三十五头,
下有九十四足,
问鸡兔各几何?试一试
<<孙子算经>>是我国古代较为普及的算书,许多问题浅显有趣.其中下卷第31题“鸡兔同笼”问题流传尤为广泛,飘洋过海传到了日本等国.这节课你有什么收获?(2)二元一次方程组及解的概念(3)列表尝试的方法求二元一次方程
组的解(1)二元一次方程及解的概念你对哪一点最感兴趣?你还有什么新的发现?我学习所以我快乐我反思所以我进步(4)数学方法:
数学思想:“列表尝试的方法”类比思想、
“逐次逼近”思想作业:
?1、?作业本8.1
2、结合生活实际,展开你的想象,
自创情境,请设计一题可用二元一
次方程组 来解决的探
究性应用题,同桌交换意见.
谢谢大家!轻轻的,我走了,正如我轻轻的来,我轻轻地点击鼠标,留下同学们的风采.
再见!谢谢同学们的热情参与!执教者:郑 丽 娇5、填表:对于方程3x+y=5,把适当的值填入表格。113/25/32-13.85(1)如果已知X的值,求Y的值,则Y=5-3X.(2)如果已知Y的值,求X的值,
今天我们在一起探究新的知识8、1二元一次方程组 你知道篮球比赛的规则吗?篮球联赛中,每场比赛都要分出胜负,每队胜一场得 2分,负一场得 1分。某队为了争取较好的名次,想在全部 22场比赛中得到40分,那么这个队胜负场数应分别是多少??解法一:设胜X场,则负(22-X)场。
根据题意得: 2X+(22-X)=40
解法二:设胜X场,负Y场。
根据题意得:X+Y=22 (1)
2X+Y=40 (2)
问题:
议一议观察:上述方程有什么共同的特点?x+y=222x+y=40含有两个未知数,并且未知数的指数
都是1的方程叫做①每个方程都含有两个未知数(X和y)②每个未知数的指数都是1定义:二元一次方程.问题:它与一元一次方程比较有什么不同呢?X+Y=22 (1)
2X+Y=40 (2)你能说说上述方程组的特点?由两个二元一次方程组成 由两个一次方程合起来, 共有两个未知数的方程组,叫做二元一次方程组。方程组各方程中同一字母必须代表同一个量
二元一次方程组定义:注意:两个方程共含有两个未知数1、根据上面的定义请每位同学分别写一个
二元一次方程和二元一次方程组,并与
同桌交流。试一试2.下列各式属于二元一次方程的有 个。
① x+y=3 ② x –2y2=3
③ 3x+4y ④
13.下列方程组是二元一次方程组的是 ( )
3x=6 x+2y=5
5x =10 z=2x-5
x –2y=4 x –y=1
y=1 x2+y2=2 {{{ABDCC分析: x,y的指数必须是1次,此
方程才是二元一次方程
分别令n+1=1,3m –2=1,
n=0, m=1 4.若方程 是二元一次
方程,则n=________,m= ________0 1满足方程且符合实际意义? 探究022121222324567892112201011131314151617181943105678910111214151617181920使二元一次方程两边的值相等的两个未
知数的值,叫做二元一次方程的解。注意:二元一次方程的解有无数个。X=5
Y=17二元一次方程的解具有:不定性与相关性。有哪些X、Y的值满足方程且符合实际意义?探究022121222324567892112201011131314151617181943105678910111214151617181920上表中哪对x,y的值是方程的解?一般地,二元一次方程组的两个方程的公共解,
叫做二元一次方程组的解。X+Y=22 (1)
2X+Y=40 (2)的解是有哪些x,y的值例1:下列各对数值中是二元一次方程 的解的有
B: C: D:变式:其中是二元一次方程组的解是( )。A,B,CBA:例2、方程A:无数个;B:一个;C:三个;D:四个。在自然数范围内的解有( )试一试D 例3、小明家外出旅游,估计需要胶卷底片120张.商店里有两种型号的胶卷:A型每卷36张底片,B型每卷12张底片.小明一共买了4卷胶卷,刚好有120张底片.如果设两种胶卷分别买x卷和y卷,请根据问题中的条件列出关于x,y的方程学以致用:解:由题意,得1233211209672,并用列表尝试的方法求两种胶卷的数量.问题1:假设有一根11米长的绳子,要把它剪成两段,问每一段多少米?问题2:如果剪成的两段长度都是正整数米,怎样剪?问题3:如果要剪成的两段,长的一段比短的一段长3米,怎样剪?问题4:如果要剪成的三段长度都是正整数米,且这三段首尾顺次
相接组成一个三角形,怎样剪?x+y=11 这个二元一次方程有无穷多个解大展身手:今有鸡兔同笼,
上有三十五头,
下有九十四足,
问鸡兔各几何?试一试
<<孙子算经>>是我国古代较为普及的算书,许多问题浅显有趣.其中下卷第31题“鸡兔同笼”问题流传尤为广泛,飘洋过海传到了日本等国.这节课你有什么收获?(2)二元一次方程组及解的概念(3)列表尝试的方法求二元一次方程
组的解(1)二元一次方程及解的概念你对哪一点最感兴趣?你还有什么新的发现?我学习所以我快乐我反思所以我进步(4)数学方法:
数学思想:“列表尝试的方法”类比思想、
“逐次逼近”思想作业:
?1、?作业本8.1
2、结合生活实际,展开你的想象,
自创情境,请设计一题可用二元一
次方程组 来解决的探
究性应用题,同桌交换意见.
谢谢大家!轻轻的,我走了,正如我轻轻的来,我轻轻地点击鼠标,留下同学们的风采.
再见!谢谢同学们的热情参与!执教者:郑 丽 娇5、填表:对于方程3x+y=5,把适当的值填入表格。113/25/32-13.85(1)如果已知X的值,求Y的值,则Y=5-3X.(2)如果已知Y的值,求X的值,
