数学人教A版(2019)选择性必修第一册2.5.1 直线与圆的位置关系(共18张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.5.1 直线与圆的位置关系(共18张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-13 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
2.5.1 直线与圆的位置关系
第二章 直线和圆的方程
探究新知
“海上生明月,天涯共此时。”,表达了诗人望月怀人的深厚情谊。在海天交于一线的天际,一轮明月慢慢升起,先是探出半个圆圆的小脑袋,然后冉冉上升,和天际线相连,再跃出海面,越来越高,展现着迷人的风采.
这个过程中,月亮看作一个圆,海天交线看作一条直线,月出的过程中也体现了直线与圆的三种位置关系:相交、相切和相离.
情景导入
探究新知
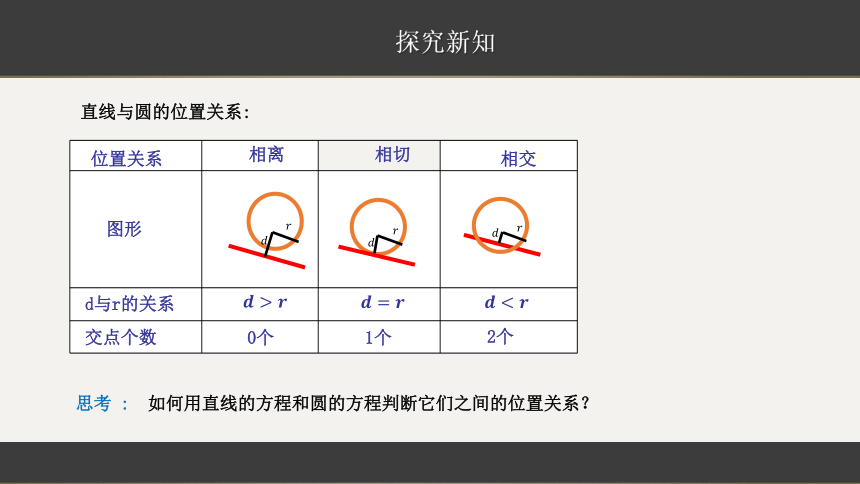
直线与圆的位置关系:
思考 : 如何用直线的方程和圆的方程判断它们之间的位置关系?
位置关系
相交
相切
相离
图形
d与r的关系
交点个数
0个
1个
2个
直线与圆的位置关系的判断
例1.如图,已知直线l: 和圆心为C的圆 ,判断直线 与圆的位置关系;如果相交,求被圆C所截得的弦长.
直线与圆的位置关系的判断
判断直线与圆位置关系的方法:
(1) 代数法:
判断直线l: Ax+By+C=0与圆C: x2+y2+Dx+Ey+F=0的位置关系, 可以联立它们的方程, 通过方程组
① △>0
消去y(或x), 得到关于x(或y)的一元二次方程.
利用一元二次方程的判别式△确定解的情况, 判断直线与圆位置关系::
直线l与圆C相交;
方程有两不等实根
② △=0
直线l与圆C相切;
方程有两个相等实根
③ △<0
直线l与圆C相离.
方程无实数根
若相交, 可以由方程组(1)解得两交点坐标利用两点间的距离公式求得弦长.
直线与圆的位置关系的判断
判断直线与圆位置关系的方法:
(2) 几何法:
根据圆的方程求得圆心到直线的距离d, 通过比较d与r的大小, 判断直线与圆的位置关系. 若相交, 则可利用勾股定理求得弦长.
已知直线l: Ax+By+C=0, 圆C: (x-a)2 + (y-b)2=r2. 设圆心C到直线l的距离为d,则有
③ d>r
① d<r
直线l与圆C相交;
② d=r
直线l与圆C相切;
直线l与圆C相离.
若直线l与圆C相交, 则弦长公式为:
直线与圆的位置关系的判断
x
y
O
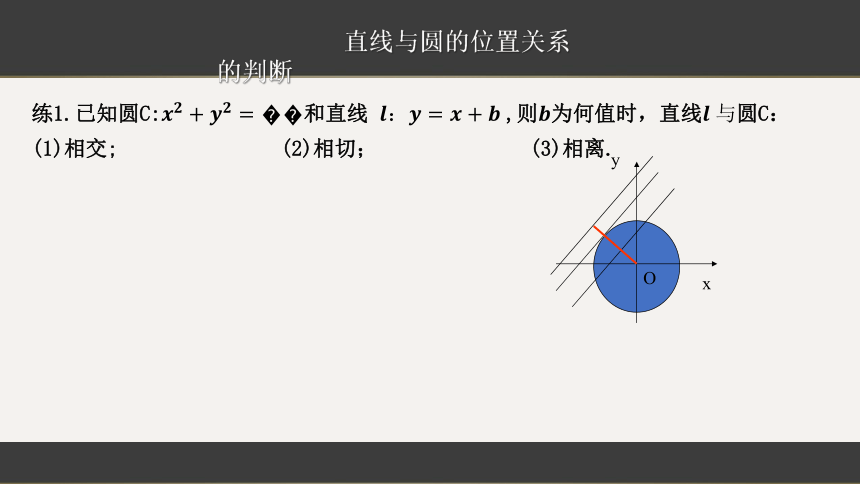
练1.已知圆C:和直线 ,则为何值时,直线圆C:
(1)相交; (2)相切; (3)相离.
圆的切线问题
例2.过点作圆的切线,求此切线的方程.
.
P
O
x
y
解法1:设切线的斜率为,则切线的方程为,
即
由圆心(0,0)到切线l的距离等于圆的半径1,得
解得或 .因此,所求切线l的方程为,或.
解法2:设切线的斜率为,则切线的方程为,
因为直线l与圆相切,所以方程组只有一组解.
消元,得.①
解得或 .
因此,所求切线l的方程为,或.
因为方程①只有一个解,所以,
圆的切线问题
练2:过点A(4,-3)作圆C:(x-3)2+(y-1)2=1的切线,求此切线的方程.
①如果已知点在圆上,那么圆心和已知点的连线和切线垂直,从而求得切线的斜率,用直线的点斜式方程可求得切线方程.
②如果已知点在圆外,过这点的切线将有两条,但在设斜率解题时要先判定斜率是否存在,否则可能会漏解.
总结:求过已知点的圆的切线的方法
圆的弦长问题
例3.直线经过点P(5,5),并且与圆C:x2+y2=25相交截得的弦长为4,求直线的方程.
法一(几何法) 若直线l的斜率不存在,则l:x=5,与圆C相切,不合题意,所以直线l的斜率存在.
设直线l的方程为y-5=k(x-5).
如图所示,|OH|是圆心到直线l的距离,|OA|是圆的半径,|AH|是弦长|AB|的一半,
在Rt△AHO中,|OA|=5,|AH|=|AB|=×4=2,
所以|OH|==,
所以=,解得k=或k=2,所以直线l的方程为x-2y+5=0或2x-y-5=0.
圆的弦长问题
例3.直线经过点P(5,5),并且与圆C:x2+y2=25相交截得的弦长为4,求直线的方程.
法二(代数法) 设直线l的方程为y-5=k(x-5),与圆C相交于点A(x1,y1),B(x2,y2),
联立方程组消去y,得(k2+1)x2+10k(1-k)x+25k(k-2)=0,
所以Δ=[10k(1-k)]2-4(k2+1)·25k(k-2)>0,解得k>0.
又x1+x2=-,x1x2=,y1-y2=k(x1-x2),
所以|AB|===
==4,
两边平方,整理得2k2-5k+2=0,解得k=或k=2,符合题意.故直线l的方程为x-2y+5=0或2x-y-5=0.
圆的弦长问题
方法总结:求弦长的方法通常有以下两种
(1)几何法:由圆的性质知,过圆心O作l的垂线,垂足C为线段AB的中点.如图所示,在Rt△OCB中,|BC|2=r2-d2,则弦长|AB|=2|BC|=2.
(2)代数法:解方程组消元后可得关于x1+x2,x1·x2或y1+y2,y1·y2的关系式,则|AB|==.
圆的弦长问题
例4.已知圆C:x2+=5,直线
(1)证明:,直线与圆C总有两个不同的交点;
(2)设直线与圆C交于A,B两点,若=,求的值.
因此所证命题成立
解法1:
A
B
l
代 数 方 法
圆的弦长问题
例4.已知圆C:x2+=5,直线
(1)证明:,直线与圆C总有两个不同的交点;
(2)设直线与圆C交于A,B两点,若=,求的值.
解法2:(1)由圆方程可知,圆心为(0,1),半径为 r =则圆心到直线 l的距离为
因此所证命题成立
r
d
几何方法
l
A
B
解法3:mx-y+1-m=0过定点(1,1)而(1,1)在圆内,所以直线与圆相交.
圆的弦长问题
例4.已知圆C:x2+=5,直线
(1)证明:,直线与圆C总有两个不同的交点;
(2)设直线与圆C交于A,B两点,若=,求的值.
(2)由垂径定理可知
变式:求直线被圆C截得的弦长最小时,直线的方程.
r
d
l
A
B
圆的弦长问题
练3.已知圆C:+=25,直线
(1)证明:,直线l与圆C总相交;
(2)求直线与圆C截得的弦长最小时,直线的方程.
圆的弦长问题
练4. 圆C:+上到直线 的距离为的点共有几个?
练5. m为何值时,直线与圆=5.
(1)无公共点; (2)截得弦长为2.
课堂小结
代数方法
几何方法
图形直观判断
两图形方程判断
直线与圆的位置关系
相交 两个交点 d相切 一个交点 d=r
相离 没有交点 d>r
有无交点,有几个.
直线l与圆C的方程组成的方程组是否有解,有几个解.
判断圆C的圆心到直线l的距离d与圆的半径r的关系(大于、小于、等于).
判断直线与圆的位置关系
2.5.1 直线与圆的位置关系
第二章 直线和圆的方程
探究新知
“海上生明月,天涯共此时。”,表达了诗人望月怀人的深厚情谊。在海天交于一线的天际,一轮明月慢慢升起,先是探出半个圆圆的小脑袋,然后冉冉上升,和天际线相连,再跃出海面,越来越高,展现着迷人的风采.
这个过程中,月亮看作一个圆,海天交线看作一条直线,月出的过程中也体现了直线与圆的三种位置关系:相交、相切和相离.
情景导入
探究新知
直线与圆的位置关系:
思考 : 如何用直线的方程和圆的方程判断它们之间的位置关系?
位置关系
相交
相切
相离
图形
d与r的关系
交点个数
0个
1个
2个
直线与圆的位置关系的判断
例1.如图,已知直线l: 和圆心为C的圆 ,判断直线 与圆的位置关系;如果相交,求被圆C所截得的弦长.
直线与圆的位置关系的判断
判断直线与圆位置关系的方法:
(1) 代数法:
判断直线l: Ax+By+C=0与圆C: x2+y2+Dx+Ey+F=0的位置关系, 可以联立它们的方程, 通过方程组
① △>0
消去y(或x), 得到关于x(或y)的一元二次方程.
利用一元二次方程的判别式△确定解的情况, 判断直线与圆位置关系::
直线l与圆C相交;
方程有两不等实根
② △=0
直线l与圆C相切;
方程有两个相等实根
③ △<0
直线l与圆C相离.
方程无实数根
若相交, 可以由方程组(1)解得两交点坐标利用两点间的距离公式求得弦长.
直线与圆的位置关系的判断
判断直线与圆位置关系的方法:
(2) 几何法:
根据圆的方程求得圆心到直线的距离d, 通过比较d与r的大小, 判断直线与圆的位置关系. 若相交, 则可利用勾股定理求得弦长.
已知直线l: Ax+By+C=0, 圆C: (x-a)2 + (y-b)2=r2. 设圆心C到直线l的距离为d,则有
③ d>r
① d<r
直线l与圆C相交;
② d=r
直线l与圆C相切;
直线l与圆C相离.
若直线l与圆C相交, 则弦长公式为:
直线与圆的位置关系的判断
x
y
O
练1.已知圆C:和直线 ,则为何值时,直线圆C:
(1)相交; (2)相切; (3)相离.
圆的切线问题
例2.过点作圆的切线,求此切线的方程.
.
P
O
x
y
解法1:设切线的斜率为,则切线的方程为,
即
由圆心(0,0)到切线l的距离等于圆的半径1,得
解得或 .因此,所求切线l的方程为,或.
解法2:设切线的斜率为,则切线的方程为,
因为直线l与圆相切,所以方程组只有一组解.
消元,得.①
解得或 .
因此,所求切线l的方程为,或.
因为方程①只有一个解,所以,
圆的切线问题
练2:过点A(4,-3)作圆C:(x-3)2+(y-1)2=1的切线,求此切线的方程.
①如果已知点在圆上,那么圆心和已知点的连线和切线垂直,从而求得切线的斜率,用直线的点斜式方程可求得切线方程.
②如果已知点在圆外,过这点的切线将有两条,但在设斜率解题时要先判定斜率是否存在,否则可能会漏解.
总结:求过已知点的圆的切线的方法
圆的弦长问题
例3.直线经过点P(5,5),并且与圆C:x2+y2=25相交截得的弦长为4,求直线的方程.
法一(几何法) 若直线l的斜率不存在,则l:x=5,与圆C相切,不合题意,所以直线l的斜率存在.
设直线l的方程为y-5=k(x-5).
如图所示,|OH|是圆心到直线l的距离,|OA|是圆的半径,|AH|是弦长|AB|的一半,
在Rt△AHO中,|OA|=5,|AH|=|AB|=×4=2,
所以|OH|==,
所以=,解得k=或k=2,所以直线l的方程为x-2y+5=0或2x-y-5=0.
圆的弦长问题
例3.直线经过点P(5,5),并且与圆C:x2+y2=25相交截得的弦长为4,求直线的方程.
法二(代数法) 设直线l的方程为y-5=k(x-5),与圆C相交于点A(x1,y1),B(x2,y2),
联立方程组消去y,得(k2+1)x2+10k(1-k)x+25k(k-2)=0,
所以Δ=[10k(1-k)]2-4(k2+1)·25k(k-2)>0,解得k>0.
又x1+x2=-,x1x2=,y1-y2=k(x1-x2),
所以|AB|===
==4,
两边平方,整理得2k2-5k+2=0,解得k=或k=2,符合题意.故直线l的方程为x-2y+5=0或2x-y-5=0.
圆的弦长问题
方法总结:求弦长的方法通常有以下两种
(1)几何法:由圆的性质知,过圆心O作l的垂线,垂足C为线段AB的中点.如图所示,在Rt△OCB中,|BC|2=r2-d2,则弦长|AB|=2|BC|=2.
(2)代数法:解方程组消元后可得关于x1+x2,x1·x2或y1+y2,y1·y2的关系式,则|AB|==.
圆的弦长问题
例4.已知圆C:x2+=5,直线
(1)证明:,直线与圆C总有两个不同的交点;
(2)设直线与圆C交于A,B两点,若=,求的值.
因此所证命题成立
解法1:
A
B
l
代 数 方 法
圆的弦长问题
例4.已知圆C:x2+=5,直线
(1)证明:,直线与圆C总有两个不同的交点;
(2)设直线与圆C交于A,B两点,若=,求的值.
解法2:(1)由圆方程可知,圆心为(0,1),半径为 r =则圆心到直线 l的距离为
因此所证命题成立
r
d
几何方法
l
A
B
解法3:mx-y+1-m=0过定点(1,1)而(1,1)在圆内,所以直线与圆相交.
圆的弦长问题
例4.已知圆C:x2+=5,直线
(1)证明:,直线与圆C总有两个不同的交点;
(2)设直线与圆C交于A,B两点,若=,求的值.
(2)由垂径定理可知
变式:求直线被圆C截得的弦长最小时,直线的方程.
r
d
l
A
B
圆的弦长问题
练3.已知圆C:+=25,直线
(1)证明:,直线l与圆C总相交;
(2)求直线与圆C截得的弦长最小时,直线的方程.
圆的弦长问题
练4. 圆C:+上到直线 的距离为的点共有几个?
练5. m为何值时,直线与圆=5.
(1)无公共点; (2)截得弦长为2.
课堂小结
代数方法
几何方法
图形直观判断
两图形方程判断
直线与圆的位置关系
相交 两个交点 d
相离 没有交点 d>r
有无交点,有几个.
直线l与圆C的方程组成的方程组是否有解,有几个解.
判断圆C的圆心到直线l的距离d与圆的半径r的关系(大于、小于、等于).
判断直线与圆的位置关系
