冀教版数学九年级下册31.4用列举法求简单事件的概率 同步练习(含答案)
文档属性
| 名称 | 冀教版数学九年级下册31.4用列举法求简单事件的概率 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 480.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-12 21:47:27 | ||
图片预览



文档简介
31.4用列举法求简单事件的概率同步练习冀教版数学九年级下册
一、单选题(共30分)
1.(本题3分)现有4张卡片,正面图案如图所示,它们除此之外完全相同.把这4张卡片背面朝上洗匀,从中随机抽取两张,则这两张卡片正面图案恰好是“天问”和“九章”的概率是( )
A. B. C. D.
2.(本题3分)某市有6名教师志愿到四川地震灾区的甲、乙、丙三个镇去支教,每人只能去一个镇,则恰好其中一镇去4名,另两镇各去1名的概率为( )
A. B. C. D.
3.(本题3分)用图中两个可自由转动的转盘做“配紫色”游戏:分别转动两个转盘,若其中一个转出红色,另一个转出蓝色,即可配成紫色(若指针指在分界线上,则重转),则配成紫色的概率为( )
A. B. C. D.
4.(本题3分)为了疫情防控,某小区需要从甲、乙、丙、丁 4名志愿者中随机抽取2名负责该小区入口处的测温工作,则甲被抽中的概率是( )
A. B. C. D.
5.(本题3分)某轨道列车共有3节车厢,设乘客从任意一节车厢上车的机会均等,某天甲、乙两位乘客同时乘同一列轨道列车,则甲和乙从同一节车厢上车的概率是( )
A. B. C. D.
6.(本题3分)掷一枚质地均匀的骰子,前3次都是6点朝上,掷第4次时6点朝上的概率是( )
A.1 B. C. D.
7.(本题3分)如图在三条横线和三条竖线组成的图形中,任选两条横线和两条竖线都可以图成一个矩形,从这些矩形中任选一个,则所选矩形含点A的概率是( )
A. B. C. D.
8.(本题3分)从甲、乙、丙三名同学中随机抽取两名同学去参加义务劳动,则甲与乙恰好被选中的概率是( )
A. B. C. D.
9.(本题3分)如图,管中放置着三根同样的绳子、、,小明先从左端A、B、C三个绳头中随机选两个打一个结,再从右端、、三个绳头中随机选两个打一个结,则这三根绳子能连接成一根长绳的概率为( )
A. B. C. D.
10.(本题3分)从-3,0,1,2这四个数中任取一个数作为一元二次方程的系数的值,能使该方程有实数根的概率是( )
A. B. C. D.
二、填空题(共30分)
11.(本题3分)布袋中有红、黄、蓝三个球,它们除颜色不同以外,其他都相同,从袋中随机取出一个球后再放回袋中,这样取出球的顺序依次是“红—黄—蓝”的概率是__________.
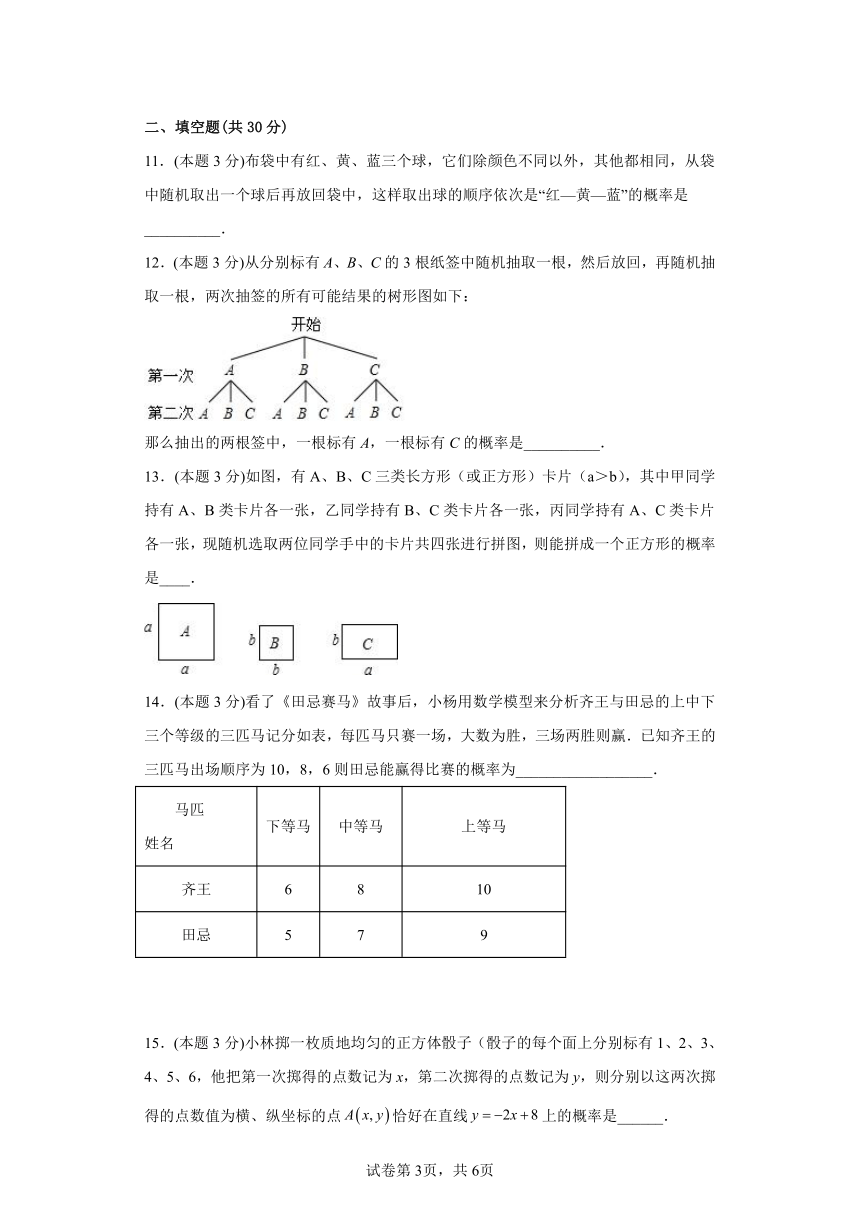
12.(本题3分)从分别标有A、B、C的3根纸签中随机抽取一根,然后放回,再随机抽取一根,两次抽签的所有可能结果的树形图如下:
那么抽出的两根签中,一根标有A,一根标有C的概率是__________.
13.(本题3分)如图,有A、B、C三类长方形(或正方形)卡片(a>b),其中甲同学持有A、B类卡片各一张,乙同学持有B、C类卡片各一张,丙同学持有A、C类卡片各一张,现随机选取两位同学手中的卡片共四张进行拼图,则能拼成一个正方形的概率是____.
14.(本题3分)看了《田忌赛马》故事后,小杨用数学模型来分析齐王与田忌的上中下三个等级的三匹马记分如表,每匹马只赛一场,大数为胜,三场两胜则赢.已知齐王的三匹马出场顺序为10,8,6则田忌能赢得比赛的概率为__________________.
马匹 姓名 下等马 中等马 上等马
齐王 6 8 10
田忌 5 7 9
15.(本题3分)小林掷一枚质地均匀的正方体骰子(骰子的每个面上分别标有1、2、3、4、5、6,他把第一次掷得的点数记为x,第二次掷得的点数记为y,则分别以这两次掷得的点数值为横、纵坐标的点恰好在直线上的概率是______.
16.(本题3分)如图,有8张标记数字1-8的卡片.甲、乙两人玩一个游戏,规则是:甲、乙两人轮流从中取走卡片;每次可以取1张,也可以取2张,还可以取3张卡片(取2张或3张卡片时,卡片上标记的数字必须连续);最后一个将卡片取完的人获胜.
若甲先取走标记2,3的卡片,乙又取走标记7,8的卡片,接着甲取走两张卡片,则________(填“甲”或“乙”)一定获胜;若甲首次取走标记数字1,2,3的卡片,乙要保证一定获胜,则乙首次取卡片的方案是________.(只填一种方案即可)
17.(本题3分)从2、6、9三个数字中任选两个,用这两个数字分别作为十位数和个位数组成一个两位数,在所有得到的两位数中随机抽取一个两位数,这个两位数是4的倍数的概率是____.
18.(本题3分)一个不透明的口袋中有三个完全相同的小球,小球上分别写有数字4、5、6,随机摸取1个小球然后放回,再随机摸取一个小球
(1)用画树状图或列表的方法表示出可能出现的所有结果;
(1)求两次抽出数字之和为奇数的概率.
19.(本题3分)小强、小亮、小文三位同学玩投硬币游戏.三人同时各投出一枚均匀硬币,若出现三个正面向上或三个反面向上,则小强赢;若出现两个正面向上和一个反面向上,则小亮赢;若出现一个正面向上和两个反面向上,则小文赢.有下列说法:①小强赢的概率最小;②小文和小亮赢的概率相等;③小文赢的概率是;④这是一个公平的游戏.其中,正确的是__________(填序号).
20.(本题3分)从,,,,,这个数中任意选一个数作为的值,则使关于的方程的解是负数,且关于的一次函数的图象不经过第一象限的概率为_______.
三、解答题(共60分)
21.(本题12分)某校开展以“奋斗百年路 启航新征程”为主题的活动来庆祝建党百年.活动分为两个阶段:第一阶段是宣讲红色故事,有以党建党史、文化传承、人物传记为素材的3个宣讲项目(分别用A、B、C表示);第二阶段是主题文艺创作,有文学创作、美术创作、舞蹈创作、音乐创作4个项目(分别用D、E、F、G表示).要求参加人员在每个阶段各随机抽取一个项目完成.若小明参加该活动,请用画树状图或列表的方法列出小明参加项目的所有可能的结果,并求小明恰好抽中项目C和E的概率.
22.(本题12分)“田忌赛马”的故事闪烁着我国古代先贤的智慧光芒.该故事的大意是:齐王有上、中、下三匹马,田忌也有上、中、下三匹马,且这六匹马在比赛中的胜负可用不等式表示如下:(注:表示A马与B马比赛,A马获胜).一天,齐王找田忌赛马,约定:每匹马都出场比赛一局,共赛三局,胜两局者获得整场比赛的胜利.面对劣势,田忌事先了解到齐王三局比赛的“出马”顺序为上马、中马、下马,并采用孙膑的策略:分别用下马、上马、中马与齐王的上马、中马、下马比赛,即借助对阵()获得了整场比赛的胜利,创造了以弱胜强的经典案例.
假设齐王事先不打探田忌的“出马”情况,试回答以下问题:
(1)如果田忌事先只打探到齐王首局将出“上马”,他首局应出哪种马才可能获得整场比赛的胜利?并求其获胜的概率;
(2)如果田忌事先无法打探到齐王各局的“出马”情况,他是否必败无疑?若是,请说明理由;若不是,请列出田忌获得整场比赛胜利的所有对阵情况,并求其获胜的概率.
23.(本题12分)在3张相同的小纸条上,分别写上条件:①四边形是菱形;②四边形有一个内角是直角;③四边形的对角线相等.将这3张小纸条做成3支签,放在一个不透明的盒子中.
(1)搅匀后从中任意抽出1支签,抽到条件①的概率是__________;
(2)搅匀后先从中任意抽出1支签(不放回),再从余下的2支签中任意抽出1支签.四边形同时满足抽到的2张小纸条上的条件,求四边形一定是正方形的概率.
24.(本题12分)甲口袋中装有2个相同的小球,它们分别写有字母A和B;乙口袋中装有3个相同的小球,它们分别写有字母C,D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I.从三个口袋中各随机取出1个小球.
(本题中,A,E,I是元音字母;B,C,D,H是辅音字母.)
(1)取出的3个小球上恰好有1个、2个和3个元音字母的概率分别是多少?
(2)取出的3个小球上全是辅音字母的概率是多少?
25.(本题12分)建国中学有7位学生的生日是10月1日,其中男生分别记为,,,,女生分别记为,,.学校准备召开国庆联欢会,计划从这7位学生中抽取学生参与联欢会的访谈活动.
(1)若任意抽取1位学生,且抽取的学生为女生的概率是 ;
(2)若先从男生中任意抽取1位,再从女生中任意抽取1位,求抽得的2位学生中至少有1位是或的概率.(请用“画树状图”或“列表”等方法写出分析过程)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
2.B
3.C
4.A
5.C
6.D
7.D
8.C
9.C
10.B
11.
12.
13.
14.
15.
16. 甲 取走标记5,6,7的卡片(答案不唯一)
17.
18.
19.①②③
20..
21.所有结果见解析,概率为
22.(1)田忌首局应出“下马”才可能在整场比赛中获胜,;(2)不是,田忌获胜的所有对阵是,,,,,,
23.(1);(2)
24.(1)P(1个元音);P(2个元音);P(3个元音);(2)P(3个辅音).
25.(1)
(2)
答案第1页,共2页
答案第1页,共2页
一、单选题(共30分)
1.(本题3分)现有4张卡片,正面图案如图所示,它们除此之外完全相同.把这4张卡片背面朝上洗匀,从中随机抽取两张,则这两张卡片正面图案恰好是“天问”和“九章”的概率是( )
A. B. C. D.
2.(本题3分)某市有6名教师志愿到四川地震灾区的甲、乙、丙三个镇去支教,每人只能去一个镇,则恰好其中一镇去4名,另两镇各去1名的概率为( )
A. B. C. D.
3.(本题3分)用图中两个可自由转动的转盘做“配紫色”游戏:分别转动两个转盘,若其中一个转出红色,另一个转出蓝色,即可配成紫色(若指针指在分界线上,则重转),则配成紫色的概率为( )
A. B. C. D.
4.(本题3分)为了疫情防控,某小区需要从甲、乙、丙、丁 4名志愿者中随机抽取2名负责该小区入口处的测温工作,则甲被抽中的概率是( )
A. B. C. D.
5.(本题3分)某轨道列车共有3节车厢,设乘客从任意一节车厢上车的机会均等,某天甲、乙两位乘客同时乘同一列轨道列车,则甲和乙从同一节车厢上车的概率是( )
A. B. C. D.
6.(本题3分)掷一枚质地均匀的骰子,前3次都是6点朝上,掷第4次时6点朝上的概率是( )
A.1 B. C. D.
7.(本题3分)如图在三条横线和三条竖线组成的图形中,任选两条横线和两条竖线都可以图成一个矩形,从这些矩形中任选一个,则所选矩形含点A的概率是( )
A. B. C. D.
8.(本题3分)从甲、乙、丙三名同学中随机抽取两名同学去参加义务劳动,则甲与乙恰好被选中的概率是( )
A. B. C. D.
9.(本题3分)如图,管中放置着三根同样的绳子、、,小明先从左端A、B、C三个绳头中随机选两个打一个结,再从右端、、三个绳头中随机选两个打一个结,则这三根绳子能连接成一根长绳的概率为( )
A. B. C. D.
10.(本题3分)从-3,0,1,2这四个数中任取一个数作为一元二次方程的系数的值,能使该方程有实数根的概率是( )
A. B. C. D.
二、填空题(共30分)
11.(本题3分)布袋中有红、黄、蓝三个球,它们除颜色不同以外,其他都相同,从袋中随机取出一个球后再放回袋中,这样取出球的顺序依次是“红—黄—蓝”的概率是__________.
12.(本题3分)从分别标有A、B、C的3根纸签中随机抽取一根,然后放回,再随机抽取一根,两次抽签的所有可能结果的树形图如下:
那么抽出的两根签中,一根标有A,一根标有C的概率是__________.
13.(本题3分)如图,有A、B、C三类长方形(或正方形)卡片(a>b),其中甲同学持有A、B类卡片各一张,乙同学持有B、C类卡片各一张,丙同学持有A、C类卡片各一张,现随机选取两位同学手中的卡片共四张进行拼图,则能拼成一个正方形的概率是____.
14.(本题3分)看了《田忌赛马》故事后,小杨用数学模型来分析齐王与田忌的上中下三个等级的三匹马记分如表,每匹马只赛一场,大数为胜,三场两胜则赢.已知齐王的三匹马出场顺序为10,8,6则田忌能赢得比赛的概率为__________________.
马匹 姓名 下等马 中等马 上等马
齐王 6 8 10
田忌 5 7 9
15.(本题3分)小林掷一枚质地均匀的正方体骰子(骰子的每个面上分别标有1、2、3、4、5、6,他把第一次掷得的点数记为x,第二次掷得的点数记为y,则分别以这两次掷得的点数值为横、纵坐标的点恰好在直线上的概率是______.
16.(本题3分)如图,有8张标记数字1-8的卡片.甲、乙两人玩一个游戏,规则是:甲、乙两人轮流从中取走卡片;每次可以取1张,也可以取2张,还可以取3张卡片(取2张或3张卡片时,卡片上标记的数字必须连续);最后一个将卡片取完的人获胜.
若甲先取走标记2,3的卡片,乙又取走标记7,8的卡片,接着甲取走两张卡片,则________(填“甲”或“乙”)一定获胜;若甲首次取走标记数字1,2,3的卡片,乙要保证一定获胜,则乙首次取卡片的方案是________.(只填一种方案即可)
17.(本题3分)从2、6、9三个数字中任选两个,用这两个数字分别作为十位数和个位数组成一个两位数,在所有得到的两位数中随机抽取一个两位数,这个两位数是4的倍数的概率是____.
18.(本题3分)一个不透明的口袋中有三个完全相同的小球,小球上分别写有数字4、5、6,随机摸取1个小球然后放回,再随机摸取一个小球
(1)用画树状图或列表的方法表示出可能出现的所有结果;
(1)求两次抽出数字之和为奇数的概率.
19.(本题3分)小强、小亮、小文三位同学玩投硬币游戏.三人同时各投出一枚均匀硬币,若出现三个正面向上或三个反面向上,则小强赢;若出现两个正面向上和一个反面向上,则小亮赢;若出现一个正面向上和两个反面向上,则小文赢.有下列说法:①小强赢的概率最小;②小文和小亮赢的概率相等;③小文赢的概率是;④这是一个公平的游戏.其中,正确的是__________(填序号).
20.(本题3分)从,,,,,这个数中任意选一个数作为的值,则使关于的方程的解是负数,且关于的一次函数的图象不经过第一象限的概率为_______.
三、解答题(共60分)
21.(本题12分)某校开展以“奋斗百年路 启航新征程”为主题的活动来庆祝建党百年.活动分为两个阶段:第一阶段是宣讲红色故事,有以党建党史、文化传承、人物传记为素材的3个宣讲项目(分别用A、B、C表示);第二阶段是主题文艺创作,有文学创作、美术创作、舞蹈创作、音乐创作4个项目(分别用D、E、F、G表示).要求参加人员在每个阶段各随机抽取一个项目完成.若小明参加该活动,请用画树状图或列表的方法列出小明参加项目的所有可能的结果,并求小明恰好抽中项目C和E的概率.
22.(本题12分)“田忌赛马”的故事闪烁着我国古代先贤的智慧光芒.该故事的大意是:齐王有上、中、下三匹马,田忌也有上、中、下三匹马,且这六匹马在比赛中的胜负可用不等式表示如下:(注:表示A马与B马比赛,A马获胜).一天,齐王找田忌赛马,约定:每匹马都出场比赛一局,共赛三局,胜两局者获得整场比赛的胜利.面对劣势,田忌事先了解到齐王三局比赛的“出马”顺序为上马、中马、下马,并采用孙膑的策略:分别用下马、上马、中马与齐王的上马、中马、下马比赛,即借助对阵()获得了整场比赛的胜利,创造了以弱胜强的经典案例.
假设齐王事先不打探田忌的“出马”情况,试回答以下问题:
(1)如果田忌事先只打探到齐王首局将出“上马”,他首局应出哪种马才可能获得整场比赛的胜利?并求其获胜的概率;
(2)如果田忌事先无法打探到齐王各局的“出马”情况,他是否必败无疑?若是,请说明理由;若不是,请列出田忌获得整场比赛胜利的所有对阵情况,并求其获胜的概率.
23.(本题12分)在3张相同的小纸条上,分别写上条件:①四边形是菱形;②四边形有一个内角是直角;③四边形的对角线相等.将这3张小纸条做成3支签,放在一个不透明的盒子中.
(1)搅匀后从中任意抽出1支签,抽到条件①的概率是__________;
(2)搅匀后先从中任意抽出1支签(不放回),再从余下的2支签中任意抽出1支签.四边形同时满足抽到的2张小纸条上的条件,求四边形一定是正方形的概率.
24.(本题12分)甲口袋中装有2个相同的小球,它们分别写有字母A和B;乙口袋中装有3个相同的小球,它们分别写有字母C,D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I.从三个口袋中各随机取出1个小球.
(本题中,A,E,I是元音字母;B,C,D,H是辅音字母.)
(1)取出的3个小球上恰好有1个、2个和3个元音字母的概率分别是多少?
(2)取出的3个小球上全是辅音字母的概率是多少?
25.(本题12分)建国中学有7位学生的生日是10月1日,其中男生分别记为,,,,女生分别记为,,.学校准备召开国庆联欢会,计划从这7位学生中抽取学生参与联欢会的访谈活动.
(1)若任意抽取1位学生,且抽取的学生为女生的概率是 ;
(2)若先从男生中任意抽取1位,再从女生中任意抽取1位,求抽得的2位学生中至少有1位是或的概率.(请用“画树状图”或“列表”等方法写出分析过程)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
2.B
3.C
4.A
5.C
6.D
7.D
8.C
9.C
10.B
11.
12.
13.
14.
15.
16. 甲 取走标记5,6,7的卡片(答案不唯一)
17.
18.
19.①②③
20..
21.所有结果见解析,概率为
22.(1)田忌首局应出“下马”才可能在整场比赛中获胜,;(2)不是,田忌获胜的所有对阵是,,,,,,
23.(1);(2)
24.(1)P(1个元音);P(2个元音);P(3个元音);(2)P(3个辅音).
25.(1)
(2)
答案第1页,共2页
答案第1页,共2页
