8.3实际问题与 二元一次方程组[下学期]
文档属性
| 名称 | 8.3实际问题与 二元一次方程组[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 731.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-04-04 00:00:00 | ||
图片预览







文档简介
课件20张PPT。8.3实际问题与
二元一次方程组教学设计教材上这节课的主要内容是用二元一次方程组来解决与生活密切相关的有一定思考性的问题.强调动手参与,从事数学探究活动.综合运用已有的知识,经过自助探索、互相交流,感受二元一次方程组在实际问题中的价值.本节课中问题一是有关数量关系分析的问题,问题二是利用图表来进行探究,问题三是方案设计问题,这三个问题从不同的方面对如何建立数学模型解决实际问题进行了探索,希望学生在探索和解决问题的过程中获得发展、获得新知识、获得数学思维能力.在我国“方程”一词最早出现于东汉初年的数学经典著作《九章算术》的第
八章“方程”.到唐、宋时期,对方程的
研究达到我国古代的鼎盛阶段,这时所创立的用“天元术”解题从设未知数到列方程和现代数学十分相似,也就是在这个时期,方程知识从中国传入日本。
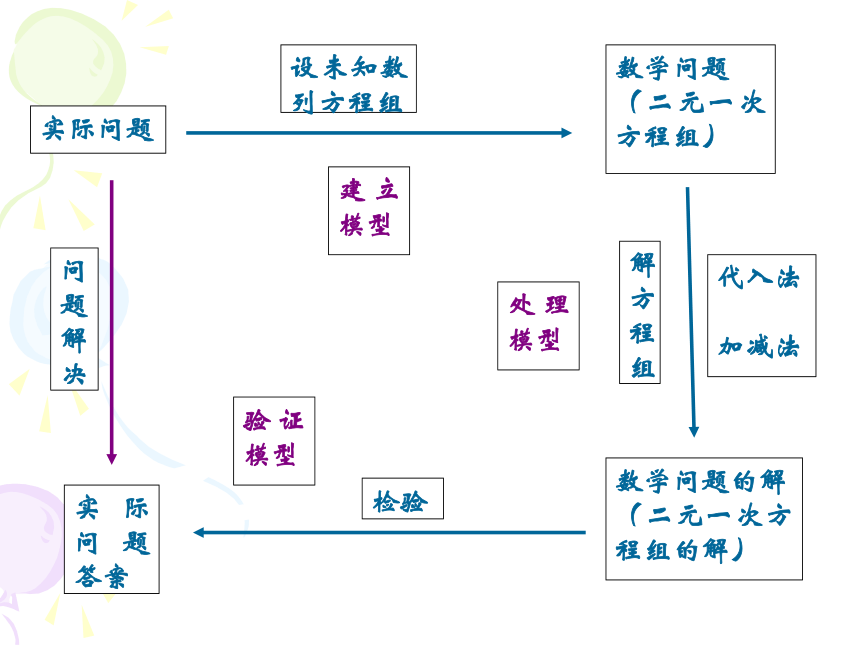
我们又该如何利用方程来解决实际问题的呢? 数学问题
(二元一次方程组)设未知数列方程组数学问题的解
(二元一次方程组的解)实际问题答案解方程组代入法
加减法检验建立模型处理模型实际问题问题解决验证模型现实中存在大量问题涉及多个未知
数,其中许多问题中的数量关系是一
次的(也称线性的)。这就使得二元
一次方程组成为解决现实问题的一种
重要的数学模型,它是解决含有多个
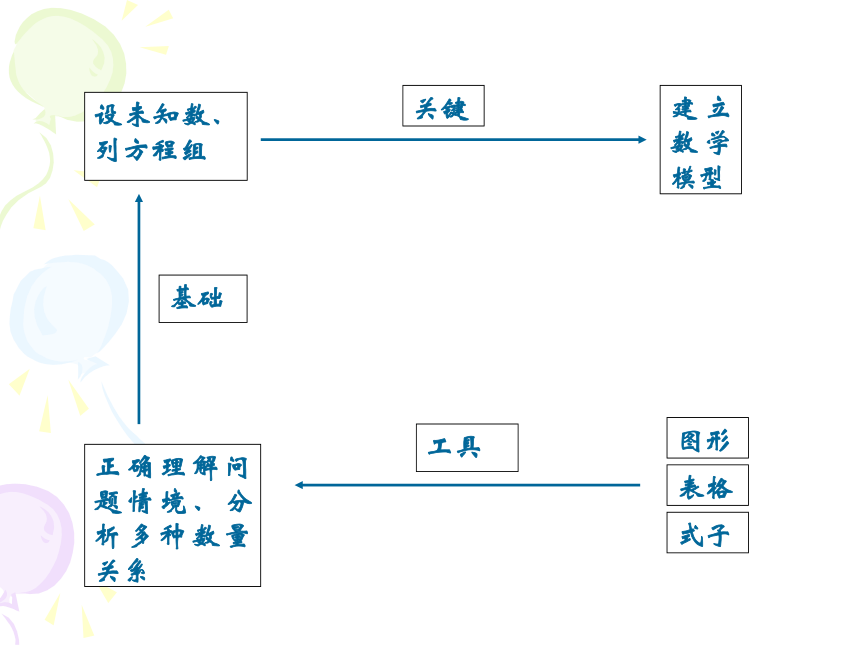
未知数问题的重要数学工具。如何建
立二元一次方程组模型呢?图形设未知数、列方程组正确理解问题情境、分析多种数量关系关键建立数学模型基础工具表格式子问题1、某班同学参加运土劳动,女同学除了1名请假外,全部分配去抬土,两人用扁担抬一筐;男生除了3名体弱者跟女生一起抬土外,其余全部去担土,1人担两筐,这样全班共需要土筐59个,扁担36根,问该班男、女生各有多少人? 思路启迪:
两个未知的数量:男生人数和女生人数
两个等量关系:
抬土扁担数 + 担土扁担数 = 36
抬土筐数 + 担土筐数 = 59
如何由男女生人数来表示这两个等量关系
呢?分析题目中的数量之间的关系成为关键。设该班男生x人,女生y人
抬土人数:y-1+3 =y+2 担土人数:x - 3
抬土扁担数: 担土扁担数:x – 3
抬土筐数: 担土筐数:2(x – 3)
答:该班男生26人,女生24人依题意,得解之,得 正确理解问题情境、分析多种数量之间的关系是列方程组建立数学模型的基础 练习1、怎样把45分成甲、乙、丙、丁
四个数,使甲数加2、乙数减2、丙数加
倍、丁数减半的结果相等?
思路启迪:本题有四个未知数,如果用四元一次方程组来解,显然太繁。
注意到“甲数加2、乙数减2”后正好相等,可知乙数=甲数+4;
又由“丙数加倍、丁数减半”后正好相等,可知:丁数=丙数×4。
因此,只需设甲数和丙数这两个未知数就便于列出方程组了现租用该公司3辆甲种货车及5辆乙种货车一次刚好运完这批货,如果按每吨付运费30元计算,问货主应付运费多少元?问题2、一批货物运往某地,货主准备租用汽车运输公司的甲、乙两种货车。已知过去两次租用这两种货车的情况如下表:思路启迪:
要求出货主应付运费数必须知道运货吨数,
运货总吨数与甲种货车、乙种货车每辆每次
运货吨数有关。
根据表中数据可以先求出甲种货车、乙种货车每辆每次运货吨数解:设甲种货车每辆每次运货x吨,乙种货车每
辆每次运货y吨根据题意,有解得30(3x+5y)=30×(3×4+5×2.5)=735(元)答:货主应付运费735元问题3、某牛奶加工厂现有鲜奶9吨,若在市场上直接销售鲜奶,每吨可获利润500元,制成酸奶销售,每吨可获利1200元,制成奶片销售,每吨可获利2000元,该厂的生产能力是:如制成酸奶每天可加工3吨;制成奶片每天可加工1吨;受条件限制,两种加工方式不能同时进行,受气温影响,牛奶必须在四天内销售或加工完毕,为此,该厂设计了两种方案:
方案一:尽可能多的制成奶片,其余直接销售鲜牛奶;
方案二:一部分制成奶片,其余全部制成酸奶,并保证在四天内完成。
你认为哪种方案获利最多?为什么?方案一、四天加工奶片为1×4(吨),
则鲜奶数量为9-4=5(吨)
所以,总利润为
1×4×2000+(9-1×4)×500
=8000+2500
=10500(元) 产品总量= 9吨 加工总天数= 4天方案二、一部分制成奶片,其余全部制成酸奶,
并保证在四天内完成。
设制成奶片x吨,制成酸奶y吨,根据题意,得解之得 所以总利润为 1.5×2000+7.5 ×1200=3000+9000
=12000(元)因为12000元>10500元,所以方案二获利多。小结:
首先要读懂题意,正确理解问题情境;
然后借助表格列出题目中出现的数量,简化题目使条件一目了然,并分析多种数量之间的关系;
最后根据题意列出方程。
这样就建立了解决实际问题的数学模型。
然后处理数学模型,得出解答,并经事实检验成为实际问题的答案。思考:
小雨去郊游,早上9时下车,先走平路,然后登山,到山顶后又沿原路返回到下车处,此时正好是下午2时,若他走平路时每小时走4千米,爬山时每小时走3千米,下山时每小时走6千米,则小雨从上午到下午一共走了多少千米?为了防沙治沙,政府决定投入资金,鼓励农民植树种草。经测算,植树1亩需资金200元,种草1亩需资金100元,某组农民计划在一年内完成2400亩绿化任务,在实施中由于实际情况所限,植树完成了计划的90%,种草超额完成了计划的20%,恰好完成了计划的绿化任务,那么所结余的资金还能植树多少亩?
谢谢!
(二元一次方程组)设未知数列方程组数学问题的解
(二元一次方程组的解)实际问题答案解方程组代入法
加减法检验建立模型处理模型实际问题问题解决验证模型现实中存在大量问题涉及多个未知
数,其中许多问题中的数量关系是一
次的(也称线性的)。这就使得二元
一次方程组成为解决现实问题的一种
重要的数学模型,它是解决含有多个
未知数问题的重要数学工具。如何建
立二元一次方程组模型呢?图形设未知数、列方程组正确理解问题情境、分析多种数量关系关键建立数学模型基础工具表格式子问题1、某班同学参加运土劳动,女同学除了1名请假外,全部分配去抬土,两人用扁担抬一筐;男生除了3名体弱者跟女生一起抬土外,其余全部去担土,1人担两筐,这样全班共需要土筐59个,扁担36根,问该班男、女生各有多少人? 思路启迪:
两个未知的数量:男生人数和女生人数
两个等量关系:
抬土扁担数 + 担土扁担数 = 36
抬土筐数 + 担土筐数 = 59
如何由男女生人数来表示这两个等量关系
呢?分析题目中的数量之间的关系成为关键。设该班男生x人,女生y人
抬土人数:y-1+3 =y+2 担土人数:x - 3
抬土扁担数: 担土扁担数:x – 3
抬土筐数: 担土筐数:2(x – 3)
答:该班男生26人,女生24人依题意,得解之,得 正确理解问题情境、分析多种数量之间的关系是列方程组建立数学模型的基础 练习1、怎样把45分成甲、乙、丙、丁
四个数,使甲数加2、乙数减2、丙数加
倍、丁数减半的结果相等?
思路启迪:本题有四个未知数,如果用四元一次方程组来解,显然太繁。
注意到“甲数加2、乙数减2”后正好相等,可知乙数=甲数+4;
又由“丙数加倍、丁数减半”后正好相等,可知:丁数=丙数×4。
因此,只需设甲数和丙数这两个未知数就便于列出方程组了现租用该公司3辆甲种货车及5辆乙种货车一次刚好运完这批货,如果按每吨付运费30元计算,问货主应付运费多少元?问题2、一批货物运往某地,货主准备租用汽车运输公司的甲、乙两种货车。已知过去两次租用这两种货车的情况如下表:思路启迪:
要求出货主应付运费数必须知道运货吨数,
运货总吨数与甲种货车、乙种货车每辆每次
运货吨数有关。
根据表中数据可以先求出甲种货车、乙种货车每辆每次运货吨数解:设甲种货车每辆每次运货x吨,乙种货车每
辆每次运货y吨根据题意,有解得30(3x+5y)=30×(3×4+5×2.5)=735(元)答:货主应付运费735元问题3、某牛奶加工厂现有鲜奶9吨,若在市场上直接销售鲜奶,每吨可获利润500元,制成酸奶销售,每吨可获利1200元,制成奶片销售,每吨可获利2000元,该厂的生产能力是:如制成酸奶每天可加工3吨;制成奶片每天可加工1吨;受条件限制,两种加工方式不能同时进行,受气温影响,牛奶必须在四天内销售或加工完毕,为此,该厂设计了两种方案:
方案一:尽可能多的制成奶片,其余直接销售鲜牛奶;
方案二:一部分制成奶片,其余全部制成酸奶,并保证在四天内完成。
你认为哪种方案获利最多?为什么?方案一、四天加工奶片为1×4(吨),
则鲜奶数量为9-4=5(吨)
所以,总利润为
1×4×2000+(9-1×4)×500
=8000+2500
=10500(元) 产品总量= 9吨 加工总天数= 4天方案二、一部分制成奶片,其余全部制成酸奶,
并保证在四天内完成。
设制成奶片x吨,制成酸奶y吨,根据题意,得解之得 所以总利润为 1.5×2000+7.5 ×1200=3000+9000
=12000(元)因为12000元>10500元,所以方案二获利多。小结:
首先要读懂题意,正确理解问题情境;
然后借助表格列出题目中出现的数量,简化题目使条件一目了然,并分析多种数量之间的关系;
最后根据题意列出方程。
这样就建立了解决实际问题的数学模型。
然后处理数学模型,得出解答,并经事实检验成为实际问题的答案。思考:
小雨去郊游,早上9时下车,先走平路,然后登山,到山顶后又沿原路返回到下车处,此时正好是下午2时,若他走平路时每小时走4千米,爬山时每小时走3千米,下山时每小时走6千米,则小雨从上午到下午一共走了多少千米?为了防沙治沙,政府决定投入资金,鼓励农民植树种草。经测算,植树1亩需资金200元,种草1亩需资金100元,某组农民计划在一年内完成2400亩绿化任务,在实施中由于实际情况所限,植树完成了计划的90%,种草超额完成了计划的20%,恰好完成了计划的绿化任务,那么所结余的资金还能植树多少亩?
谢谢!
