3.1函数的单调性 课件(共40张PPT)
文档属性
| 名称 | 3.1函数的单调性 课件(共40张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-13 15:12:54 | ||
图片预览










文档简介
(共40张PPT)
§3 函数的单调性和最值
3.1 函数的单调性
核心知识目标 核心素养目标
1.从图象直观、定性描述和定量分析三个方面,认识函数的单调性,理解函数单调性的定义.
2.会用函数单调性的定义判断(或证明)一些函数的单调性,会求一些具体函数的单调区间. 1.通过单调区间、单调性等概念的学习,培养抽象概括素养.
2.通过用定义证明函数的单调性,培养逻辑推理素养.
知识探究·素养培育
探究点一
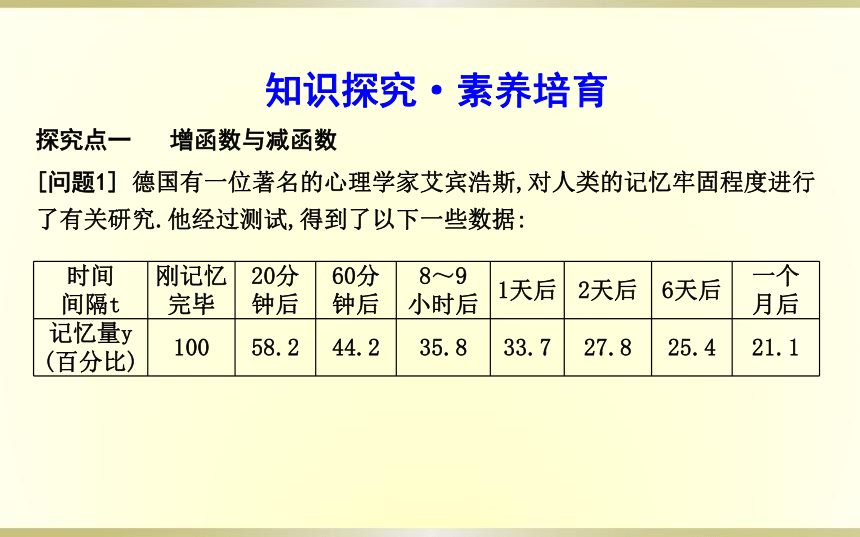
[问题1] 德国有一位著名的心理学家艾宾浩斯,对人类的记忆牢固程度进行了有关研究.他经过测试,得到了以下一些数据:
增函数与减函数
时间
间隔t 刚记忆
完毕 20分
钟后 60分
钟后 8~9
小时后 1天后 2天后 6天后 一个
月后
记忆量y
(百分比) 100 58.2 44.2 35.8 33.7 27.8 25.4 21.1
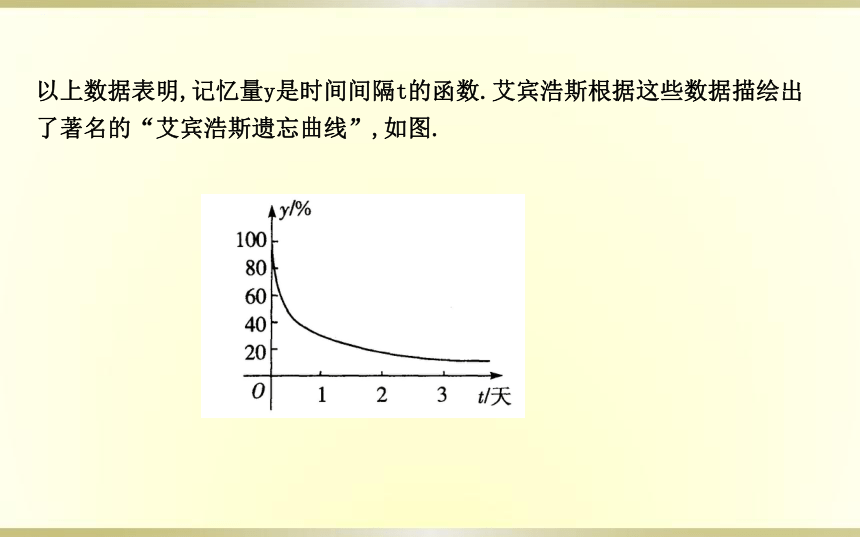
以上数据表明,记忆量y是时间间隔t的函数.艾宾浩斯根据这些数据描绘出了著名的“艾宾浩斯遗忘曲线”,如图.
(1)当时间间隔t逐渐增大,你能看出对应的函数值y有什么变化趋势 通过这个试验,你打算以后如何对待刚学过的知识
(2)“艾宾浩斯遗忘曲线”从左至右是逐渐下降的,对此,我们如何用数学观点进行解释
提示:(1)随着时间间隔t逐渐增大,函数值y逐渐变小,这个试验告诉我们,在学习中,我们应及时复习刚学习过的知识.
(2)“艾宾浩斯遗忘曲线”是减函数曲线.
知识点1:增函数与减函数的定义
设函数y=f(x)的定义域是D:
如果对于任意的x1,x2∈D,当x1如果对于任意的x1,x2∈D,当x1f(x2),那么就称函数y=f(x)是 函数.特别地,当I是定义域D上的一个区间时,也称函数y=f(x)在区间I上 .
增
单调递增
减
单调递减
(2)当x≥1时,f(x)单调递增,
当x<1时,f(x)单调递减,
所以f(x)的定义域为(-∞,1),[1,+∞).
并且函数f(x)在(-∞,1)上单调递减,在[1,+∞)上单调递增.
[例1] 求下列函数的定义域,并指出该函数在其定义域(或其定义域上的不同区间)上单调递增还是单调递减.
(3)f(x)=-x2+2|x|+3.
变式训练1-1:讨论函数f(x)=-(x-3)|x|的单调性.
方法总结
判断函数单调性的方法
(1)利用基本初等函数的单调性,如本例(1)和(2),其中分段函数的单调性要根据函数的自变量的取值范围分段求解;
(2)利用函数的图象.
探究点二
函数的单调性
知识点2:函数的单调性
如果函数y=f(x)在区间I上单调递增或单调递减,那么就称函数y=f(x)在区间I上具有单调性.此时,区间I为函数y=f(x)的 .
单调区间
[思考2] 已知函数f(x)与g(x)在公共区间上具有单调性,
(1)若函数f(x)与g(x)均为增函数,那么F(x)=f(x)+g(x)的单调性如何
(2)若函数f(x)为增函数,g(x)为减函数,那么F(x)=f(x)-g(x)的单调性如何
(3)若函数f(x)为减函数,g(x)为减函数,那么F(x)=f(x)+g(x)的单调性如何
(4)若函数f(x)为减函数,g(x)为增函数,那么F(x)=f(x)-g(x)的单调性如何
提示:(1)F(x)=f(x)+g(x)单调递增;
(2)F(x)=f(x)-g(x)单调递增;
(3)F(x)=f(x)+g(x)单调递减;
(4)F(x)=f(x)-g(x)单调递减.
(2)判断函数f(x)在(1,+∞)上的单调性,并加以证明.
(2)试判断函数在(-1,+∞)上的单调性,并给予证明.
方法总结
证明函数f(x)在区间D上的单调性的步骤
(1)在区间D上任取两个自变量的值x1,x2,并规定 x1(2)计算f(x1)-f(x2),将f(x1)-f(x2)分解为若干个可以直接确定符号的式子;
(3)确定f(x1)-f(x2)的符号.若f(x1)-f(x2)<0,则函数f(x)在区间D上单调递增;若f(x1)-f(x2)>0,则函数f(x)在区间D上单调递减.
易错警示
证明单调性的步骤中,作差f(x1)-f(x2)变形时,应注意若函数解析式是多项式,常将差式变形后提取公因式.若f(x)解析式含分式,需将分式通分后变形.若f(x)的解析式含根式,常将“差式”进行有理化变形.
探究点三
单调性的应用
[问题3] (1)若函数f(x)是其定义域上的增函数,且f(a)>f(b),则a,b满足什么关系 如果函数f(x)是减函数呢
(2)决定一元二次函数f(x)=ax2+bx+c单调性的因素有哪些
提示:(1)若函数f(x)是其定义域上的增函数,那么当f(a)>f(b)时,a>b;若函数f(x)是其定义域上的减函数,那么当f(a)>f(b)时,a答案:(1)C
(2)已知二次函数f(x)=x2-6ax+1.
①若函数f(x)的一个单调区间是(-∞,6],则a的取值集合是 ;
②若函数f(x)在(-∞,6]上是减函数,则a的取值集合是 .
解析:(2)①因为f(x)=x2-6ax+1的单调递减区间是(-∞,3a],
又由题意知f(x)的一个单调区间是(-∞,6],所以3a=6,所以a=2.
所以满足条件的a的取值集合是{2}.
②因为f(x)=x2-6ax+1的单调递减区间是(-∞,3a],
又f(x)在(-∞,6]上是减函数,所以3a≥6,所以a≥2.
所以a的取值集合是{a|a≥2}.
答案:(2)①{2} ②{a|a≥2}
变式训练3-1:(1)若函数f(x)=x2+2(a-1)x+2a2-1在区间[-2,2]上是单调函数,则实数a的取值范围是( )
(A)(-∞,-1] (B)[-1,3]
(C)[3,+∞) (D)[3,+∞)∪(-∞,-1]
解析:(1)因为函数f(x)=x2+2(a-1)x+2a2-1的图象开口向上,对称轴方程为x=1-a,
又因为f(x)=x2+2(a-1)x+2a2-1在区间[-2,2]上是单调函数,
所以1-a≥2或1-a≤-2,
解得a≥3或a≤-1.故选D.
方法总结
函数单调性的应用
(1)若一个函数在区间[a,b]上是单调的,则此函数在这一单调区间内的任意子集上也是单调的.注意函数在某个区间I上单调与函数的单调区间是I的区别.前者是函数相应单调区间的子集,而后者就是函数的单调区间.
(2)对于分段函数在实数集R上的单调递增(减)问题,除了保证在定义域的每一个区间上单调性相同之外,还要考虑在分界点处的函数值的大小关系.若函数是增函数,则左边函数值小于或等于右边函数值(若函数是减函数,则右边函数值小于或等于左边函数值),这样才能满足R上的单调递增(减),否则求出的参数范围会出现错误.
拓展探索素养培优
复合函数的单调性
复合函数y=f(g(x)),若u=g(x)在给定的区间(a,b)上是单调函数且y=f(u)在(g(a),g(b))或(g(b),g(a)) 上也是单调函数,则复合函数y=f(g(x))在(a,b)上是单调函数.
①若u=g(x),y=f(u)在所讨论的区间上都是增函数或都是减函数,则y=f(g(x))为增函数;
②若u=g(x),y=f(u)在所讨论的区间上一个是增函数,另一个是减函数,则y=f(g(x))为减函数.
列表如下:
内层函数
u=g(x) 外层函数
y=f(u) 复合函数
y=f(g(x))
增函数 增函数 增函数
增函数 减函数 减函数
减函数 增函数 减函数
减函数 减函数 增函数
复合函数的单调性可简记为“同增异减”,即内外层函数的单调性相同时,复合函数单调递增,相异时单调递减.
(2)函数f(x)是定义在R上的增函数,则函数f(|x-2|)的单调递减区间是
( )
(A)(-∞,2] (B)(-∞,-2]
(C)[2,+∞) (D)R
解析:(2)函数f(|x-2|)可以写成内外层函数y=f(t),t=|x-2|,
内层函数在(-∞,2]上单调递减,在(2,+∞)上单调递增,
外层函数是增函数,可知函数f(|x-2|)在区间(-∞,2]上单调递减.
故选A.
备用例题
解析:由题意知,函数f(x)在R上为增函数,
当x≥a时,f(x)=|x2-2x-3|的图象如图所示.
因为f(x)在R上为增函数,所以a≥3.
当x0,
且在x=a处a2-2a-3≥a2-11,解得a≤4,
综上,3≤a≤4.故选C.
(2)判断y=f(x)在(0,+∞)上的单调性,并给出你的证明;
(3)解不等式f(x2)>f(8x-6)-1.
点击进入 课时训练·分层突破
§3 函数的单调性和最值
3.1 函数的单调性
核心知识目标 核心素养目标
1.从图象直观、定性描述和定量分析三个方面,认识函数的单调性,理解函数单调性的定义.
2.会用函数单调性的定义判断(或证明)一些函数的单调性,会求一些具体函数的单调区间. 1.通过单调区间、单调性等概念的学习,培养抽象概括素养.
2.通过用定义证明函数的单调性,培养逻辑推理素养.
知识探究·素养培育
探究点一
[问题1] 德国有一位著名的心理学家艾宾浩斯,对人类的记忆牢固程度进行了有关研究.他经过测试,得到了以下一些数据:
增函数与减函数
时间
间隔t 刚记忆
完毕 20分
钟后 60分
钟后 8~9
小时后 1天后 2天后 6天后 一个
月后
记忆量y
(百分比) 100 58.2 44.2 35.8 33.7 27.8 25.4 21.1
以上数据表明,记忆量y是时间间隔t的函数.艾宾浩斯根据这些数据描绘出了著名的“艾宾浩斯遗忘曲线”,如图.
(1)当时间间隔t逐渐增大,你能看出对应的函数值y有什么变化趋势 通过这个试验,你打算以后如何对待刚学过的知识
(2)“艾宾浩斯遗忘曲线”从左至右是逐渐下降的,对此,我们如何用数学观点进行解释
提示:(1)随着时间间隔t逐渐增大,函数值y逐渐变小,这个试验告诉我们,在学习中,我们应及时复习刚学习过的知识.
(2)“艾宾浩斯遗忘曲线”是减函数曲线.
知识点1:增函数与减函数的定义
设函数y=f(x)的定义域是D:
如果对于任意的x1,x2∈D,当x1
增
单调递增
减
单调递减
(2)当x≥1时,f(x)单调递增,
当x<1时,f(x)单调递减,
所以f(x)的定义域为(-∞,1),[1,+∞).
并且函数f(x)在(-∞,1)上单调递减,在[1,+∞)上单调递增.
[例1] 求下列函数的定义域,并指出该函数在其定义域(或其定义域上的不同区间)上单调递增还是单调递减.
(3)f(x)=-x2+2|x|+3.
变式训练1-1:讨论函数f(x)=-(x-3)|x|的单调性.
方法总结
判断函数单调性的方法
(1)利用基本初等函数的单调性,如本例(1)和(2),其中分段函数的单调性要根据函数的自变量的取值范围分段求解;
(2)利用函数的图象.
探究点二
函数的单调性
知识点2:函数的单调性
如果函数y=f(x)在区间I上单调递增或单调递减,那么就称函数y=f(x)在区间I上具有单调性.此时,区间I为函数y=f(x)的 .
单调区间
[思考2] 已知函数f(x)与g(x)在公共区间上具有单调性,
(1)若函数f(x)与g(x)均为增函数,那么F(x)=f(x)+g(x)的单调性如何
(2)若函数f(x)为增函数,g(x)为减函数,那么F(x)=f(x)-g(x)的单调性如何
(3)若函数f(x)为减函数,g(x)为减函数,那么F(x)=f(x)+g(x)的单调性如何
(4)若函数f(x)为减函数,g(x)为增函数,那么F(x)=f(x)-g(x)的单调性如何
提示:(1)F(x)=f(x)+g(x)单调递增;
(2)F(x)=f(x)-g(x)单调递增;
(3)F(x)=f(x)+g(x)单调递减;
(4)F(x)=f(x)-g(x)单调递减.
(2)判断函数f(x)在(1,+∞)上的单调性,并加以证明.
(2)试判断函数在(-1,+∞)上的单调性,并给予证明.
方法总结
证明函数f(x)在区间D上的单调性的步骤
(1)在区间D上任取两个自变量的值x1,x2,并规定 x1
(3)确定f(x1)-f(x2)的符号.若f(x1)-f(x2)<0,则函数f(x)在区间D上单调递增;若f(x1)-f(x2)>0,则函数f(x)在区间D上单调递减.
易错警示
证明单调性的步骤中,作差f(x1)-f(x2)变形时,应注意若函数解析式是多项式,常将差式变形后提取公因式.若f(x)解析式含分式,需将分式通分后变形.若f(x)的解析式含根式,常将“差式”进行有理化变形.
探究点三
单调性的应用
[问题3] (1)若函数f(x)是其定义域上的增函数,且f(a)>f(b),则a,b满足什么关系 如果函数f(x)是减函数呢
(2)决定一元二次函数f(x)=ax2+bx+c单调性的因素有哪些
提示:(1)若函数f(x)是其定义域上的增函数,那么当f(a)>f(b)时,a>b;若函数f(x)是其定义域上的减函数,那么当f(a)>f(b)时,a
(2)已知二次函数f(x)=x2-6ax+1.
①若函数f(x)的一个单调区间是(-∞,6],则a的取值集合是 ;
②若函数f(x)在(-∞,6]上是减函数,则a的取值集合是 .
解析:(2)①因为f(x)=x2-6ax+1的单调递减区间是(-∞,3a],
又由题意知f(x)的一个单调区间是(-∞,6],所以3a=6,所以a=2.
所以满足条件的a的取值集合是{2}.
②因为f(x)=x2-6ax+1的单调递减区间是(-∞,3a],
又f(x)在(-∞,6]上是减函数,所以3a≥6,所以a≥2.
所以a的取值集合是{a|a≥2}.
答案:(2)①{2} ②{a|a≥2}
变式训练3-1:(1)若函数f(x)=x2+2(a-1)x+2a2-1在区间[-2,2]上是单调函数,则实数a的取值范围是( )
(A)(-∞,-1] (B)[-1,3]
(C)[3,+∞) (D)[3,+∞)∪(-∞,-1]
解析:(1)因为函数f(x)=x2+2(a-1)x+2a2-1的图象开口向上,对称轴方程为x=1-a,
又因为f(x)=x2+2(a-1)x+2a2-1在区间[-2,2]上是单调函数,
所以1-a≥2或1-a≤-2,
解得a≥3或a≤-1.故选D.
方法总结
函数单调性的应用
(1)若一个函数在区间[a,b]上是单调的,则此函数在这一单调区间内的任意子集上也是单调的.注意函数在某个区间I上单调与函数的单调区间是I的区别.前者是函数相应单调区间的子集,而后者就是函数的单调区间.
(2)对于分段函数在实数集R上的单调递增(减)问题,除了保证在定义域的每一个区间上单调性相同之外,还要考虑在分界点处的函数值的大小关系.若函数是增函数,则左边函数值小于或等于右边函数值(若函数是减函数,则右边函数值小于或等于左边函数值),这样才能满足R上的单调递增(减),否则求出的参数范围会出现错误.
拓展探索素养培优
复合函数的单调性
复合函数y=f(g(x)),若u=g(x)在给定的区间(a,b)上是单调函数且y=f(u)在(g(a),g(b))或(g(b),g(a)) 上也是单调函数,则复合函数y=f(g(x))在(a,b)上是单调函数.
①若u=g(x),y=f(u)在所讨论的区间上都是增函数或都是减函数,则y=f(g(x))为增函数;
②若u=g(x),y=f(u)在所讨论的区间上一个是增函数,另一个是减函数,则y=f(g(x))为减函数.
列表如下:
内层函数
u=g(x) 外层函数
y=f(u) 复合函数
y=f(g(x))
增函数 增函数 增函数
增函数 减函数 减函数
减函数 增函数 减函数
减函数 减函数 增函数
复合函数的单调性可简记为“同增异减”,即内外层函数的单调性相同时,复合函数单调递增,相异时单调递减.
(2)函数f(x)是定义在R上的增函数,则函数f(|x-2|)的单调递减区间是
( )
(A)(-∞,2] (B)(-∞,-2]
(C)[2,+∞) (D)R
解析:(2)函数f(|x-2|)可以写成内外层函数y=f(t),t=|x-2|,
内层函数在(-∞,2]上单调递减,在(2,+∞)上单调递增,
外层函数是增函数,可知函数f(|x-2|)在区间(-∞,2]上单调递减.
故选A.
备用例题
解析:由题意知,函数f(x)在R上为增函数,
当x≥a时,f(x)=|x2-2x-3|的图象如图所示.
因为f(x)在R上为增函数,所以a≥3.
当x
且在x=a处a2-2a-3≥a2-11,解得a≤4,
综上,3≤a≤4.故选C.
(2)判断y=f(x)在(0,+∞)上的单调性,并给出你的证明;
(3)解不等式f(x2)>f(8x-6)-1.
点击进入 课时训练·分层突破
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
