2021-2022学年高一上学期数学人教A版(2019)必修第一册2.3.1一元二次不等式的解法 课件(15张PPT)
文档属性
| 名称 | 2021-2022学年高一上学期数学人教A版(2019)必修第一册2.3.1一元二次不等式的解法 课件(15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 825.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-13 15:22:59 | ||
图片预览






文档简介
2.3.1 一元二次不等式解法
1.会结合二次函数的图象,判断一元二次方程实根的存在性及实根的个数.
2.了解二次函数零点与一元二次方程根的关系.
3.能借助二次函数求解一元二次不等式,并能用集合表示一元二次不等式的解集.
学习目标
新知学习
函数、方程、不等式知识回顾
在初中,我们从一次函数的角度看一元一次方程,一元一次不等式,
发现了三者之间的内在联系,利用这种联系可以让我们更简便的解决问题:
?
?
?
?
?
?
?
对于二次函数、一元二次方程和一元二次不等式,
他们的联系又是怎样的呢?
?
?
?
在初中,我们学习了从一次函数的观点看一元一次次方程、一元一次不等式的思想方法.类似的,能否从二次函数的观点来看一元二次不等式,进而得到
一元二次不等式的求解方法呢?
?
?
?
【注意】零点不是点,是交点的横坐标,是数
二次函数的零点
(2,0 )
(10,0 ).
图像与x轴有两个交点.它们的横坐标就是方程 的两个实根_____,____,即交点坐标为_____和_____,我们把使得 的实数x叫做函数 的零点.所以函数 的零点就是 ____, _____.
观察一下一元二次不等式 和二次函数 的关系.如图在坐标系中画出二次函数的图像,
?
?
?
?
?
?
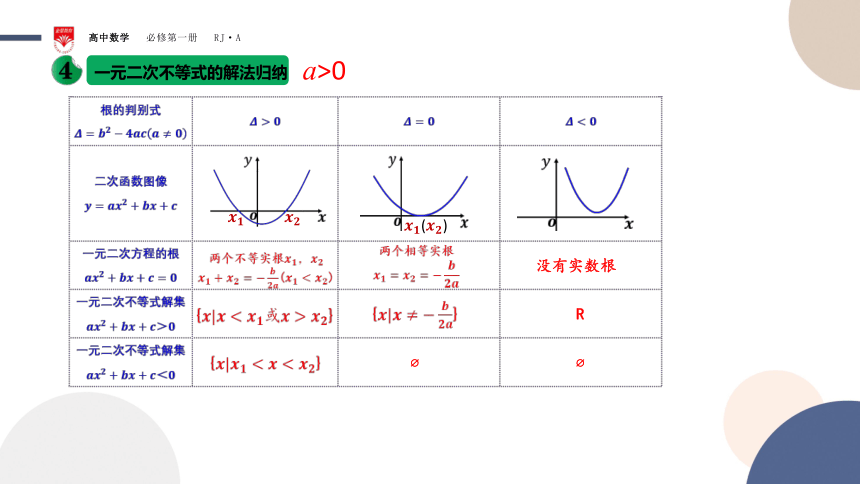
一元二次不等式的解法
上述方法可以推广到求一元二次不等式ax2+bx+c>0(a>0),ax2+bx+c<0(a>0)的解集吗?
一元二次不等式的解法归纳
????????
?
????????
?
????????(????????)
?
?
?
没有实数根
?
?
R
?
?
?
a>0
二次函数y=x2-5x的图象如图所示.
(1)若y>0,则x满足的条件是________;
(2)若y≤0,则x满足的条件是________.
即时巩固
x<0或x>5
0≤x≤5
?
?
?
?
?
?
?
?
?
例题赏析
5、
解不含参数的一元二次不等式的一般步骤
(1)化标准.通过对不等式的变形,使不等式右侧为0,使二次项系数为正.
(2)判别式.对不等式左侧因式分解,若不易分解,则计算对应方程的判别式.
(3)求实根.求出相应的一元二次方程的根或根据判别式说明方程有无实根.
(4)画草图.根据一元二次方程根的情况画出对应的二次函数的草图.
(5)写解集.根据图象写出不等式的解集.
(1) x2-5x+6<0;
解 ∵Δ=(-5)2-4×1×6=1>0,
∴方程x2-5x+6=0
有两个不相等的实数根:x1=2,x2=3.
由二次函数y=x2-5x+6的图象,
得原不等式的解集为{x|2巩固练习
(2) - x2+4x - 5<0.
解 原不等式可化为x2-4x+5>0
∵Δ=16-20=-4<0,
∴方程x2-4x+5=0无实根,
函数y=x2-4x+5的图象是开口向上的抛物线,与x轴无交点.
观察图象可得,不等式的解集为R.
(3)4x2-4x+1>0;
作出函数y=4x2-4x+1的图象如图.
解:∵Δ=16-16=0,
∴方程4x2-4x+1=0有两个相等的实数根 ,
课堂小结
本节课你有什么收获?还存在哪些困惑?
7、
课时分层作业(十四)A组
作业
8、
?
?
【解含参数的一元二次不等式】
?
?
?
?
?
挑战自我 力争满分
1.会结合二次函数的图象,判断一元二次方程实根的存在性及实根的个数.
2.了解二次函数零点与一元二次方程根的关系.
3.能借助二次函数求解一元二次不等式,并能用集合表示一元二次不等式的解集.
学习目标
新知学习
函数、方程、不等式知识回顾
在初中,我们从一次函数的角度看一元一次方程,一元一次不等式,
发现了三者之间的内在联系,利用这种联系可以让我们更简便的解决问题:
?
?
?
?
?
?
?
对于二次函数、一元二次方程和一元二次不等式,
他们的联系又是怎样的呢?
?
?
?
在初中,我们学习了从一次函数的观点看一元一次次方程、一元一次不等式的思想方法.类似的,能否从二次函数的观点来看一元二次不等式,进而得到
一元二次不等式的求解方法呢?
?
?
?
【注意】零点不是点,是交点的横坐标,是数
二次函数的零点
(2,0 )
(10,0 ).
图像与x轴有两个交点.它们的横坐标就是方程 的两个实根_____,____,即交点坐标为_____和_____,我们把使得 的实数x叫做函数 的零点.所以函数 的零点就是 ____, _____.
观察一下一元二次不等式 和二次函数 的关系.如图在坐标系中画出二次函数的图像,
?
?
?
?
?
?
一元二次不等式的解法
上述方法可以推广到求一元二次不等式ax2+bx+c>0(a>0),ax2+bx+c<0(a>0)的解集吗?
一元二次不等式的解法归纳
????????
?
????????
?
????????(????????)
?
?
?
没有实数根
?
?
R
?
?
?
a>0
二次函数y=x2-5x的图象如图所示.
(1)若y>0,则x满足的条件是________;
(2)若y≤0,则x满足的条件是________.
即时巩固
x<0或x>5
0≤x≤5
?
?
?
?
?
?
?
?
?
例题赏析
5、
解不含参数的一元二次不等式的一般步骤
(1)化标准.通过对不等式的变形,使不等式右侧为0,使二次项系数为正.
(2)判别式.对不等式左侧因式分解,若不易分解,则计算对应方程的判别式.
(3)求实根.求出相应的一元二次方程的根或根据判别式说明方程有无实根.
(4)画草图.根据一元二次方程根的情况画出对应的二次函数的草图.
(5)写解集.根据图象写出不等式的解集.
(1) x2-5x+6<0;
解 ∵Δ=(-5)2-4×1×6=1>0,
∴方程x2-5x+6=0
有两个不相等的实数根:x1=2,x2=3.
由二次函数y=x2-5x+6的图象,
得原不等式的解集为{x|2
(2) - x2+4x - 5<0.
解 原不等式可化为x2-4x+5>0
∵Δ=16-20=-4<0,
∴方程x2-4x+5=0无实根,
函数y=x2-4x+5的图象是开口向上的抛物线,与x轴无交点.
观察图象可得,不等式的解集为R.
(3)4x2-4x+1>0;
作出函数y=4x2-4x+1的图象如图.
解:∵Δ=16-16=0,
∴方程4x2-4x+1=0有两个相等的实数根 ,
课堂小结
本节课你有什么收获?还存在哪些困惑?
7、
课时分层作业(十四)A组
作业
8、
?
?
【解含参数的一元二次不等式】
?
?
?
?
?
挑战自我 力争满分
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
