一次函数和二元一次方程组[上学期]
文档属性
| 名称 | 一次函数和二元一次方程组[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 510.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2005-11-10 18:41:00 | ||
图片预览




文档简介
课件23张PPT。一次函数与二元一次方程(组)3x+5y=8这是什么?一次函数?这两个问题给我们什么启示?二元一次方程?思
考
与
研
讨 1.一次函数与二元一次方程的关系以方程 x+y=3 的解为坐标的所有点组成的图
象就是 的图象.二元一次方程 3x+5y=8 用 x 的式子表示 y一次函数 的图象上所有
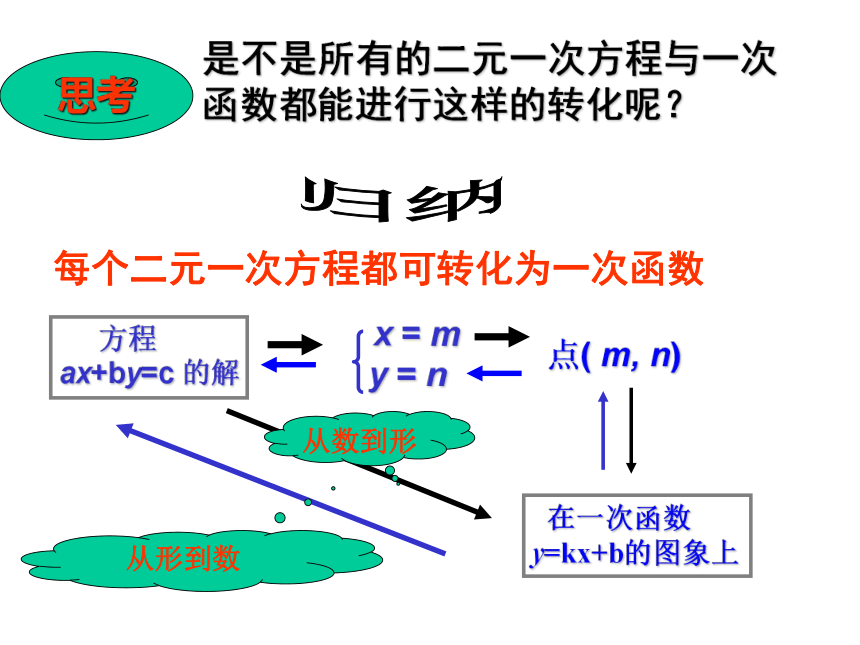
坐标都是二元一次方程3x+5y=8解 即: ,y是x的一次函数一次函数 归纳每个二元一次方程都可转化为一次函数 在一次函数
y=kx+b的图象上点( m, n) 方程
ax+by=c 的解从数到形
是不是所有的二元一次方程与一次
函数都能进行这样的转化呢?思考2. 二元一次方程组与一次函数的关系 二元一次方程组的解就是求直线y=-0.6x+1.6和直线y=2x-1的交点坐标.
求方程组的解就是求
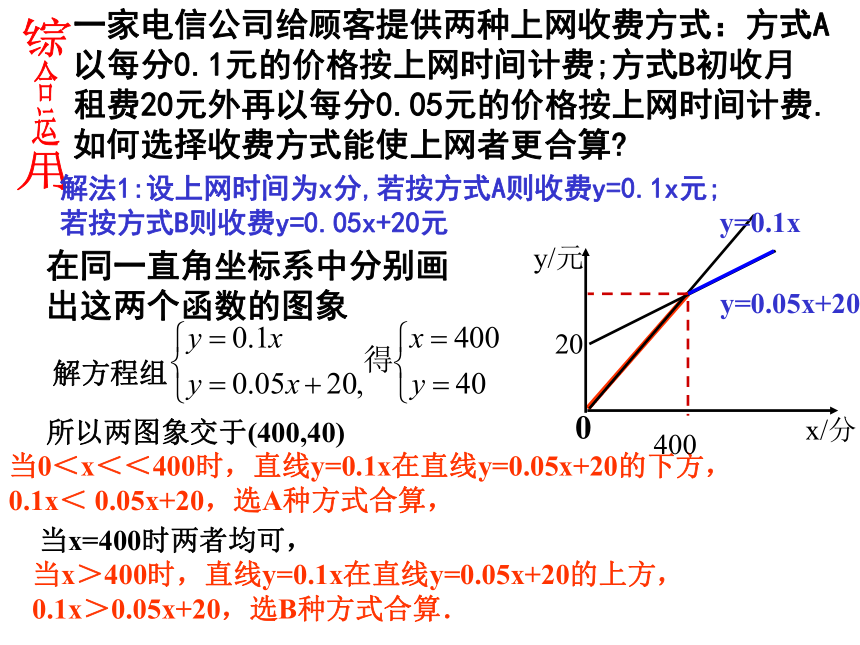
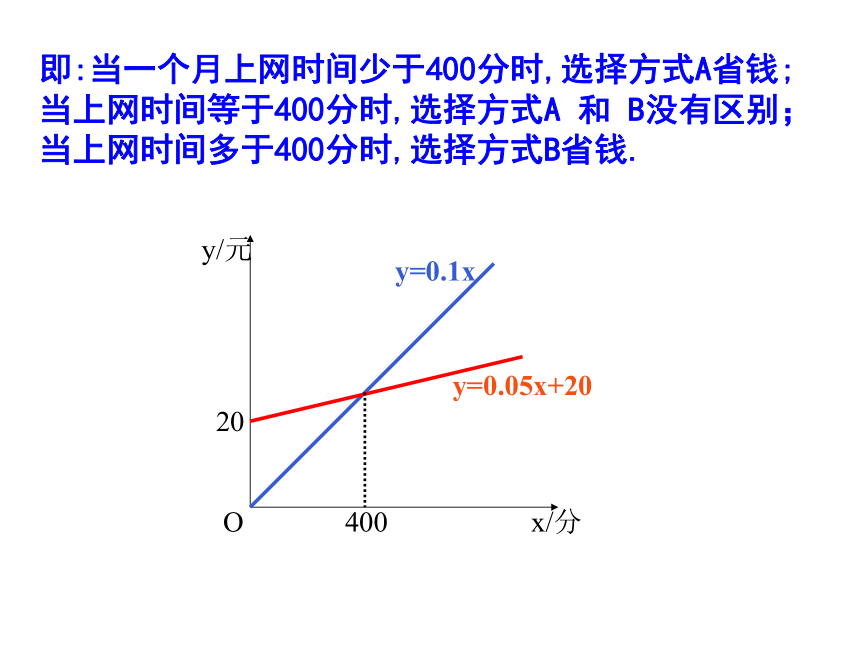
两个函数值相等时自变量的值和函数值xP(1,1)y=2x-1y y=-0.6x+1.6即:-0.6x+1.6=2x-1得x =1y =1x =1y =1解方程组由图象得从“形”的角度: 从“数”角度:根据下列图象,你能说出哪个方程组的解?这些解是什么?(1)xyO-21y=x+3学以致用我一定能行(2)yxO- 4y= - x - 4根据下列图象,你能说出哪个方程组的解?这些解是什么?综合运用一家电信公司给顾客提供两种上网收费方式:方式A以每分0.1元的价格按上网时间计费;方式B初收月租费20元外再以每分0.05元的价格按上网时间计费.如何选择收费方式能使上网者更合算?解法1:设上网时间为x分,若按方式A则收费y=0.1x元;若按方式B则收费y=0.05x+20元在同一直角坐标系中分别画出这两个函数的图象解方程组所以两图象交于(400,40)当0<x<<400时,直线y=0.1x在直线y=0.05x+20的下方, 0.1x< 0.05x+20,选A种方式合算,当x=400时两者均可,当x>400时,直线y=0.1x在直线y=0.05x+20的上方, 0.1x>0.05x+20,选B种方式合算.即:当一个月上网时间少于400分时,选择方式A省钱;当上网时间等于400分时,选择方式A 和 B没有区别;当上网时间多于400分时,选择方式B省钱.解法2:设上网时间为x分,方式A与方式B两种计费差额为y元,画出这个函数的图象400解方程-0.05x+200=0,得x=400,所以图象与x轴交点为(400,0)由图象可知:当x=400时,y=0,两者均可;当x>400时,y>0,选B方式合算
展
现
自
我
因此,当一个月上网时间少于400分时,选择方式A省钱;当上网时间
等于400分时,选择方式A 和 B没有区别;当上网时间多于400分时,
选择方式B省钱.
当0<x<400时,y>0,选A方式合算
则y与x的函数关系式为:y=(0.05x+20) -0.1x
即:y =-0.05x+200
议一议 A,B两地相距100千米,甲、乙两人骑车同时分别从A,B两地相向而行。假设他们都保持匀速行驶,则他们各自到A地的距离s(千米)都是骑车时间t(时)的一次函数。1时后乙距离A地80千米;2时后甲距离A地30千米。问经过多长时间两人将相遇?佳佳1232080100406012030甲乙 观察图像,说说你所了解到得 信息112-1猜想0.511.55202510153022.57.522.5如图,直线a, b分别表示甲走路与乙骑自行车(在同一条路上)行走的路程s与时间t的关系,观察图象并回答下列问题:补充题ab0.511.55202510153022.57.522.5(1)乙出发时,与甲相距 ;补充题10千米ab(2)走了一段路程后,乙的自行车发生故障,停下来修理,修车的时间为 ___ 小时.10.511.55202510153022.57.522.5(3)乙从出发起,经过 小时与甲相遇;补充题2.50.511.55202510153022.57.522.5(4)甲行走的路程s(km)与时间t(h)之间的函数关系是 .补充题(1)对应关系 ①将方程组中各方程化为y=kx+b的形式;
②画出各个一次函数的图象;
③由交点坐标得出方程组的解. (2)图象法解方程组的步骤:谈一谈你的收获你掌握了吗?(3) 数形结合思想的综合运用再见我学习 我快乐!1、理解一次函数与二元一次方程组的关系,会用图象法解二元一次方程组;
2. 学习用函数的观点看待方程组的方法,进一步感受数形结合的思想方法;
3. 经历图象法解方程组的探究过程,学习用联系的观点看待数学问题的辩证思想。 你掌握了吗?求直线 与 直线的交点坐标。你有哪些方法?与同伴交流,并一起分析各种方法的利弊. 解法思路2:由解方程组,得到交点坐标.(把形的问题归结为数的解决,便捷准确)
解法思路l:画出图象找出交点,确定交点坐标近似值.(因作图误差可能有较大差别)探究利用函数图象解二元一次方程组例题讲解解: 转化为在同一坐标系分别画出
和y=–3x+5的图象由图象可得
方程组的解:
考
与
研
讨 1.一次函数与二元一次方程的关系以方程 x+y=3 的解为坐标的所有点组成的图
象就是 的图象.二元一次方程 3x+5y=8 用 x 的式子表示 y一次函数 的图象上所有
坐标都是二元一次方程3x+5y=8解 即: ,y是x的一次函数一次函数 归纳每个二元一次方程都可转化为一次函数 在一次函数
y=kx+b的图象上点( m, n) 方程
ax+by=c 的解从数到形
是不是所有的二元一次方程与一次
函数都能进行这样的转化呢?思考2. 二元一次方程组与一次函数的关系 二元一次方程组的解就是求直线y=-0.6x+1.6和直线y=2x-1的交点坐标.
求方程组的解就是求
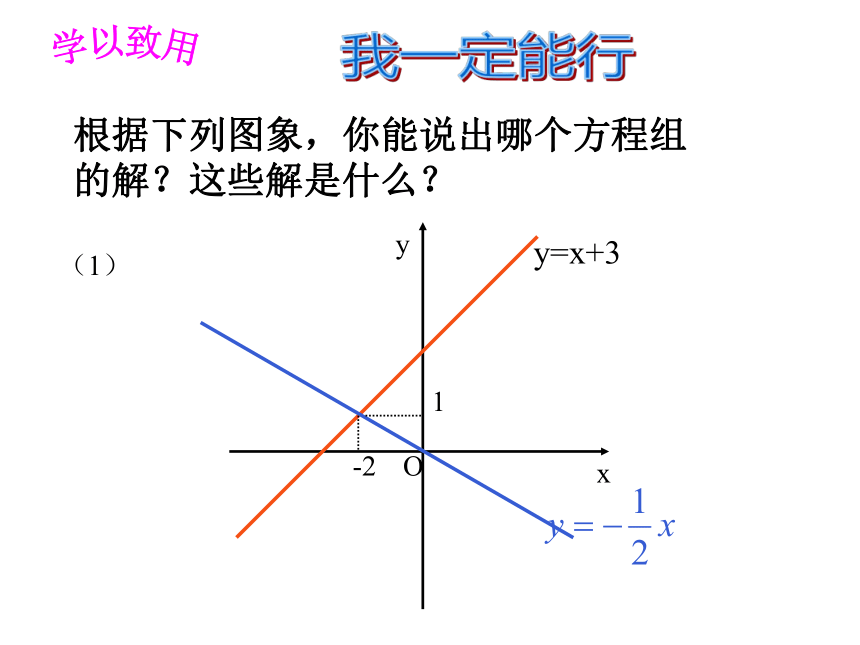
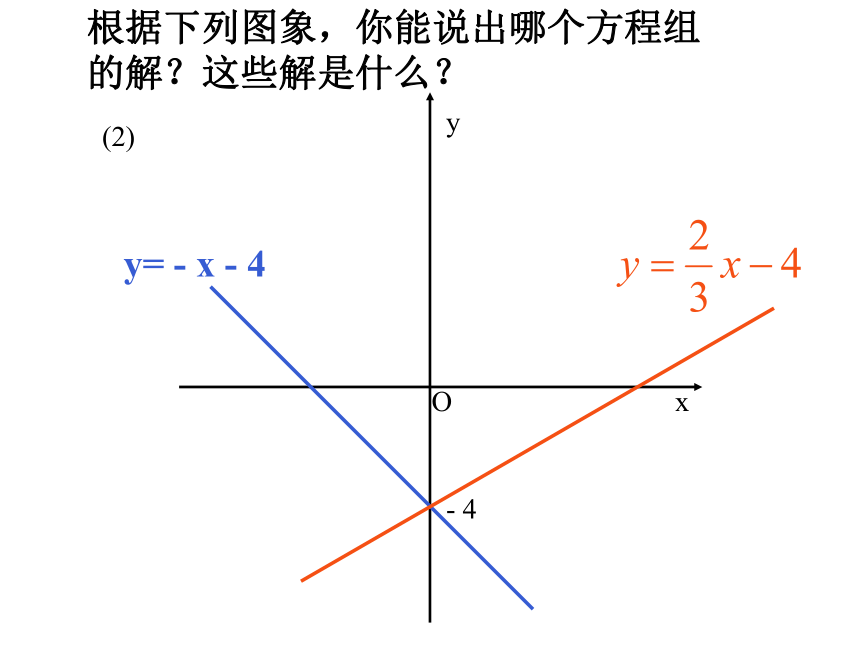
两个函数值相等时自变量的值和函数值xP(1,1)y=2x-1y y=-0.6x+1.6即:-0.6x+1.6=2x-1得x =1y =1x =1y =1解方程组由图象得从“形”的角度: 从“数”角度:根据下列图象,你能说出哪个方程组的解?这些解是什么?(1)xyO-21y=x+3学以致用我一定能行(2)yxO- 4y= - x - 4根据下列图象,你能说出哪个方程组的解?这些解是什么?综合运用一家电信公司给顾客提供两种上网收费方式:方式A以每分0.1元的价格按上网时间计费;方式B初收月租费20元外再以每分0.05元的价格按上网时间计费.如何选择收费方式能使上网者更合算?解法1:设上网时间为x分,若按方式A则收费y=0.1x元;若按方式B则收费y=0.05x+20元在同一直角坐标系中分别画出这两个函数的图象解方程组所以两图象交于(400,40)当0<x<<400时,直线y=0.1x在直线y=0.05x+20的下方, 0.1x< 0.05x+20,选A种方式合算,当x=400时两者均可,当x>400时,直线y=0.1x在直线y=0.05x+20的上方, 0.1x>0.05x+20,选B种方式合算.即:当一个月上网时间少于400分时,选择方式A省钱;当上网时间等于400分时,选择方式A 和 B没有区别;当上网时间多于400分时,选择方式B省钱.解法2:设上网时间为x分,方式A与方式B两种计费差额为y元,画出这个函数的图象400解方程-0.05x+200=0,得x=400,所以图象与x轴交点为(400,0)由图象可知:当x=400时,y=0,两者均可;当x>400时,y>0,选B方式合算
展
现
自
我
因此,当一个月上网时间少于400分时,选择方式A省钱;当上网时间
等于400分时,选择方式A 和 B没有区别;当上网时间多于400分时,
选择方式B省钱.
当0<x<400时,y>0,选A方式合算
则y与x的函数关系式为:y=(0.05x+20) -0.1x
即:y =-0.05x+200
议一议 A,B两地相距100千米,甲、乙两人骑车同时分别从A,B两地相向而行。假设他们都保持匀速行驶,则他们各自到A地的距离s(千米)都是骑车时间t(时)的一次函数。1时后乙距离A地80千米;2时后甲距离A地30千米。问经过多长时间两人将相遇?佳佳1232080100406012030甲乙 观察图像,说说你所了解到得 信息112-1猜想0.511.55202510153022.57.522.5如图,直线a, b分别表示甲走路与乙骑自行车(在同一条路上)行走的路程s与时间t的关系,观察图象并回答下列问题:补充题ab0.511.55202510153022.57.522.5(1)乙出发时,与甲相距 ;补充题10千米ab(2)走了一段路程后,乙的自行车发生故障,停下来修理,修车的时间为 ___ 小时.10.511.55202510153022.57.522.5(3)乙从出发起,经过 小时与甲相遇;补充题2.50.511.55202510153022.57.522.5(4)甲行走的路程s(km)与时间t(h)之间的函数关系是 .补充题(1)对应关系 ①将方程组中各方程化为y=kx+b的形式;
②画出各个一次函数的图象;
③由交点坐标得出方程组的解. (2)图象法解方程组的步骤:谈一谈你的收获你掌握了吗?(3) 数形结合思想的综合运用再见我学习 我快乐!1、理解一次函数与二元一次方程组的关系,会用图象法解二元一次方程组;
2. 学习用函数的观点看待方程组的方法,进一步感受数形结合的思想方法;
3. 经历图象法解方程组的探究过程,学习用联系的观点看待数学问题的辩证思想。 你掌握了吗?求直线 与 直线的交点坐标。你有哪些方法?与同伴交流,并一起分析各种方法的利弊. 解法思路2:由解方程组,得到交点坐标.(把形的问题归结为数的解决,便捷准确)
解法思路l:画出图象找出交点,确定交点坐标近似值.(因作图误差可能有较大差别)探究利用函数图象解二元一次方程组例题讲解解: 转化为在同一坐标系分别画出
和y=–3x+5的图象由图象可得
方程组的解:
