华师大版数学七年级上册 5.1.1 对顶角 课件(共24张PPT)
文档属性
| 名称 | 华师大版数学七年级上册 5.1.1 对顶角 课件(共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-13 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
第5章 相交线与平行线
5.1 相交线
第1课时 对顶角
1
课堂讲解
对顶角的定义、对顶角的性质
2
课时流程
逐点
导讲练
课堂小结
作业提升
1
知识点
对顶角的定义
定义:两个角具有相同的顶点,并且一个角的两边与
另一个角的两边互为反向延长线,我们把这样的两个
角叫做对顶角.如图,∠1和∠3是对顶角,∠2和∠4
也是对顶角.
知1-讲
知1-讲
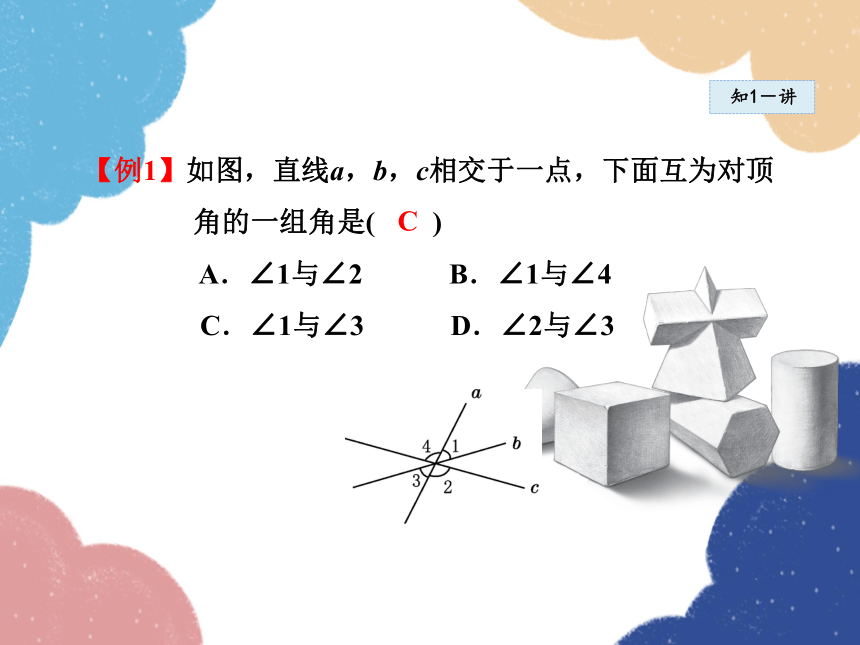
【例1】如图,直线a,b,c相交于一点,下面互为对顶
角的一组角是( )
A.∠1与∠2 B.∠1与∠4
C.∠1与∠3 D.∠2与∠3
C
知1-讲
导引:判断两个角是不是对顶角,要紧扣对顶角的定
义:∠1与∠2仅一边互为反向延长线,因此不
是对顶角;∠1与∠4的两边都不互为反向延长
线,因此不是对顶角;∠1与∠3符合对顶角的
定义;∠2与∠3的两边都不互为反向延长线,
因此也不是对顶角.
总 结
知1-讲
判断两个角是否互为对顶角的方法:一看它们有
没有公共顶点;二看这两个角的两边是否互为反向延
长线,实质就是看这两个角是否是两条直线相交所成
的没有公共边的两个角.
知1-练
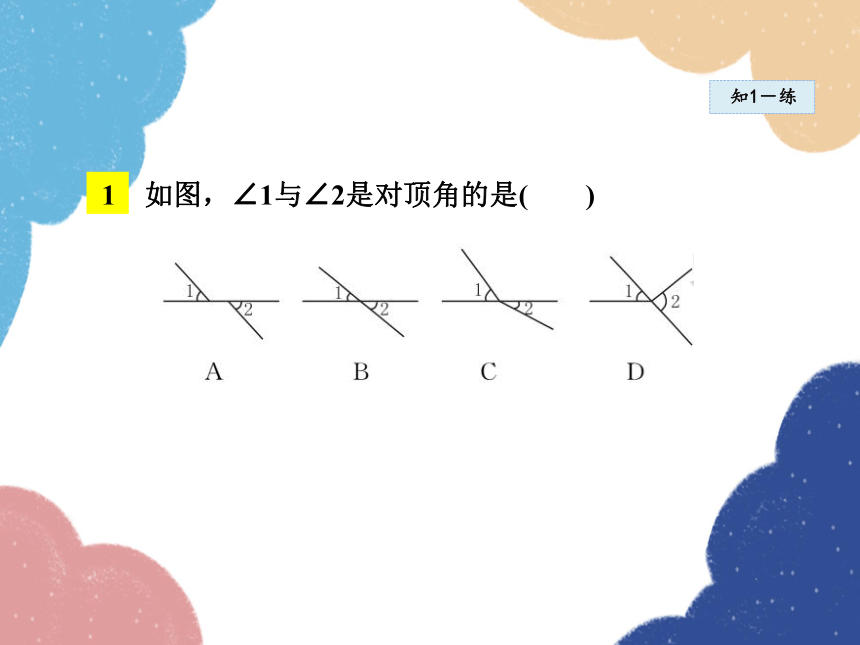
1 如图,∠1与∠2是对顶角的是( )
2 下列语句正确的是( )
A. 顶点相对的两个角是对顶角
B. 有公共顶点并且相等的两个角是对顶角
C. 两条直线相交,有公共顶点的两个角是对顶角
D. 两条直线相交,有公共顶点且没有公共边的两个
角是对顶角
知1-练
4 如图,直线AB,CD,EF相交于点O,
则图中共有_____对对顶角.
3 如图,下列各组角中,是对顶角的一组
是( )
A.∠1和∠2 B.∠3和∠5
C.∠3和∠4 D.∠1和∠5
知1-练
2
知识点
对顶角的性质
知2-导
【例2】在图中,∠1=30。,那么∠2、∠3和∠4 各等
于多少度?图中存在哪些相等关系?
解:∠2 = 180°-∠1 =180°-30° = 150°,
∠3 = 180°- ∠2 = 180°-150° =30°,
∠4 = 180°-∠1 =180°-30° = 150°.
由此,我们得到
∠1 = ∠3,∠2 =∠4.
归 纳
知2-导
对顶角的性质:对顶角相等.
知2-讲
【例3】如图,直线AB、CD相交于点E,∠AEC=50。,求
∠BED的度数.
解:因为直线AB、CD相交于点
E,所以∠AEC与∠BED是
对顶角.根据对顶角相等,得
∠BED =∠AEC = 50°.
(来自教材)
知2-讲
【例4】如图,已知直线AB,CD,EF相交于点O, ∠DOE
=90°,∠AOE=36°,求∠BOC的度数.
导引:因为∠BOC=∠AOD,∠BOC
=∠BOF+∠COF,所以有两
种途径;求∠AOD或∠BOF,
∠COF;而它们都可由已知∠DOE
=90°,∠AOE=36°求出.
解法一:因为直线AB、CD相交于点O,
所以∠BOC=∠AOD(对顶角相等).
因为∠DOE=90°,∠AOE=36°,
所以∠AOD=∠DOE+∠AOE=90°+36°=126°.
所以∠BOC=∠AOD=126°.
解法二:因为直线AB,CD,EF相交于点O,
所以∠COF=∠DOE,∠BOF=∠AOE(对顶角相等).
因为∠DOE=90°, ∠AOE=36°,
所以∠COF=90°, ∠BOF=36°.
所以∠BOC=∠COF+∠BOF =126°.
知2-讲
总 结
知2-讲
在进行计算或证明时,“对顶角相等”这个结论
常常被用来将要求的角和特征相同的两个角转化成与
已知条件相关的角;即对顶角构建了一个已知条件和
待求结论之间的“桥梁”.
知2-讲
【例5】如图,OC平分∠AOB,反向延长OC至D,反向
延长OA至E,∠3=25°,求∠BOE的度数.
导引:由图可知∠BOE+∠AOB=
180°,故要求∠BOE的度
数,只需求出∠AOB的度数
即可.因为OC平分∠AOB,即∠AOB=2∠2,
所以只需求出∠2的度数即可求出∠AOB的度数.
解:由对顶角相等,得∠2=∠3=25°.
因为OC平分∠AOB,
所以∠AOB=2∠2=50°.
又因为∠BOE与∠AOB互为邻补角,
所以∠BOE=180°-∠AOB=180°-50°=130°.
知2-讲
总 结
知2-讲
本例把两直线相交所成的角与角平分线有机地结
合在一起,通过邻补角及对顶角反映不同位置上的角
之间的关系,求角及证明相关角之间的关系是解决几
何问题的一种重要手段.
知2-练
1 如图,直线 AB,CD相交于点O,若∠1=30°,则
∠2,∠3的度数分别为( )
A.120°,60° B.130°,50°
C.140°,40° D.150°,30°
2 如图,三条直线AB,CD,EF相交于一点O,则
∠AOE+∠DOB+∠COF等于( )
A.150° B.180° C.210° D.120°
知2-练
3 如图,直线AB,CD相交于点O,∠AOC=75°,
OE把∠BOD分成两部分,且∠BOE∶∠EOD=
1∶2,则∠AOE=( )
A.165° B.155°
C.150° D.130°
知2-练
4 图中是对顶角量角器,用它测量角的
原理是____________________________.
知2-练
(1)对顶角都是成对出现的,当两个角互为对顶角时,其中
一个角叫做另一个角的对顶角;
(2)对顶角的两边互为反向延长线即在同一直线上,其实质
是:对顶角是两直线相交所成的没有公共边的两个角;
(3)对顶角的条件:①有公共顶点;②两边互为反向延长线.
(4)互为对顶角的两个角相等,但相等的两个角不一定是对
顶角.
第5章 相交线与平行线
5.1 相交线
第1课时 对顶角
1
课堂讲解
对顶角的定义、对顶角的性质
2
课时流程
逐点
导讲练
课堂小结
作业提升
1
知识点
对顶角的定义
定义:两个角具有相同的顶点,并且一个角的两边与
另一个角的两边互为反向延长线,我们把这样的两个
角叫做对顶角.如图,∠1和∠3是对顶角,∠2和∠4
也是对顶角.
知1-讲
知1-讲
【例1】如图,直线a,b,c相交于一点,下面互为对顶
角的一组角是( )
A.∠1与∠2 B.∠1与∠4
C.∠1与∠3 D.∠2与∠3
C
知1-讲
导引:判断两个角是不是对顶角,要紧扣对顶角的定
义:∠1与∠2仅一边互为反向延长线,因此不
是对顶角;∠1与∠4的两边都不互为反向延长
线,因此不是对顶角;∠1与∠3符合对顶角的
定义;∠2与∠3的两边都不互为反向延长线,
因此也不是对顶角.
总 结
知1-讲
判断两个角是否互为对顶角的方法:一看它们有
没有公共顶点;二看这两个角的两边是否互为反向延
长线,实质就是看这两个角是否是两条直线相交所成
的没有公共边的两个角.
知1-练
1 如图,∠1与∠2是对顶角的是( )
2 下列语句正确的是( )
A. 顶点相对的两个角是对顶角
B. 有公共顶点并且相等的两个角是对顶角
C. 两条直线相交,有公共顶点的两个角是对顶角
D. 两条直线相交,有公共顶点且没有公共边的两个
角是对顶角
知1-练
4 如图,直线AB,CD,EF相交于点O,
则图中共有_____对对顶角.
3 如图,下列各组角中,是对顶角的一组
是( )
A.∠1和∠2 B.∠3和∠5
C.∠3和∠4 D.∠1和∠5
知1-练
2
知识点
对顶角的性质
知2-导
【例2】在图中,∠1=30。,那么∠2、∠3和∠4 各等
于多少度?图中存在哪些相等关系?
解:∠2 = 180°-∠1 =180°-30° = 150°,
∠3 = 180°- ∠2 = 180°-150° =30°,
∠4 = 180°-∠1 =180°-30° = 150°.
由此,我们得到
∠1 = ∠3,∠2 =∠4.
归 纳
知2-导
对顶角的性质:对顶角相等.
知2-讲
【例3】如图,直线AB、CD相交于点E,∠AEC=50。,求
∠BED的度数.
解:因为直线AB、CD相交于点
E,所以∠AEC与∠BED是
对顶角.根据对顶角相等,得
∠BED =∠AEC = 50°.
(来自教材)
知2-讲
【例4】如图,已知直线AB,CD,EF相交于点O, ∠DOE
=90°,∠AOE=36°,求∠BOC的度数.
导引:因为∠BOC=∠AOD,∠BOC
=∠BOF+∠COF,所以有两
种途径;求∠AOD或∠BOF,
∠COF;而它们都可由已知∠DOE
=90°,∠AOE=36°求出.
解法一:因为直线AB、CD相交于点O,
所以∠BOC=∠AOD(对顶角相等).
因为∠DOE=90°,∠AOE=36°,
所以∠AOD=∠DOE+∠AOE=90°+36°=126°.
所以∠BOC=∠AOD=126°.
解法二:因为直线AB,CD,EF相交于点O,
所以∠COF=∠DOE,∠BOF=∠AOE(对顶角相等).
因为∠DOE=90°, ∠AOE=36°,
所以∠COF=90°, ∠BOF=36°.
所以∠BOC=∠COF+∠BOF =126°.
知2-讲
总 结
知2-讲
在进行计算或证明时,“对顶角相等”这个结论
常常被用来将要求的角和特征相同的两个角转化成与
已知条件相关的角;即对顶角构建了一个已知条件和
待求结论之间的“桥梁”.
知2-讲
【例5】如图,OC平分∠AOB,反向延长OC至D,反向
延长OA至E,∠3=25°,求∠BOE的度数.
导引:由图可知∠BOE+∠AOB=
180°,故要求∠BOE的度
数,只需求出∠AOB的度数
即可.因为OC平分∠AOB,即∠AOB=2∠2,
所以只需求出∠2的度数即可求出∠AOB的度数.
解:由对顶角相等,得∠2=∠3=25°.
因为OC平分∠AOB,
所以∠AOB=2∠2=50°.
又因为∠BOE与∠AOB互为邻补角,
所以∠BOE=180°-∠AOB=180°-50°=130°.
知2-讲
总 结
知2-讲
本例把两直线相交所成的角与角平分线有机地结
合在一起,通过邻补角及对顶角反映不同位置上的角
之间的关系,求角及证明相关角之间的关系是解决几
何问题的一种重要手段.
知2-练
1 如图,直线 AB,CD相交于点O,若∠1=30°,则
∠2,∠3的度数分别为( )
A.120°,60° B.130°,50°
C.140°,40° D.150°,30°
2 如图,三条直线AB,CD,EF相交于一点O,则
∠AOE+∠DOB+∠COF等于( )
A.150° B.180° C.210° D.120°
知2-练
3 如图,直线AB,CD相交于点O,∠AOC=75°,
OE把∠BOD分成两部分,且∠BOE∶∠EOD=
1∶2,则∠AOE=( )
A.165° B.155°
C.150° D.130°
知2-练
4 图中是对顶角量角器,用它测量角的
原理是____________________________.
知2-练
(1)对顶角都是成对出现的,当两个角互为对顶角时,其中
一个角叫做另一个角的对顶角;
(2)对顶角的两边互为反向延长线即在同一直线上,其实质
是:对顶角是两直线相交所成的没有公共边的两个角;
(3)对顶角的条件:①有公共顶点;②两边互为反向延长线.
(4)互为对顶角的两个角相等,但相等的两个角不一定是对
顶角.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
