3.4 第3课时分段计费与方案决策问题 课件(共19张PPT)
文档属性
| 名称 | 3.4 第3课时分段计费与方案决策问题 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 974.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-13 13:36:18 | ||
图片预览




文档简介
(共19张PPT)
3.4 第3课时
分段计费与方案决策问题
人教版 七年级上册
教学目标
教学目标:
1.掌握应用方程解决实际问题的方法步骤,提高分析问题、解决问题的能力。
2.通过探索球赛积分表中数量关系的过程,进一步体会方程是解决实际问题的数学模型,并且明确用方程解决实际问题时,不仅要注意解方程的过程是否正确,还要检验方程的解是否符合问题的实际意义。
3.鼓励学生自主探究,合作交流,养成自觉反思的良好习惯。
重点:把实际问题转化为数学问题,不仅会列方程求出问题的解,还会进行推理判断.
难点:把实际问题转化为数学问题.
新知导入
我市某县城为鼓励居民节约用水,对自来水用户按分段计费方式收取水费,若每月用水量不超过7 m3,则按每立方米1元收费;若每月用水量超过7 m3,则超过部分按每立方米2元收费.如果某户居民今年5月份缴纳了17元水费,那么这户居民今年5月份的用水量为多少立方米?
解:设5月份用水量为x m3,
则超出7 m3的部分为(x-7)m3.
根据题意,得7×1+(x-7)×2=17,
解得x=12.
答:这户居民今年5月份的用水量为12 m3.
新知讲解
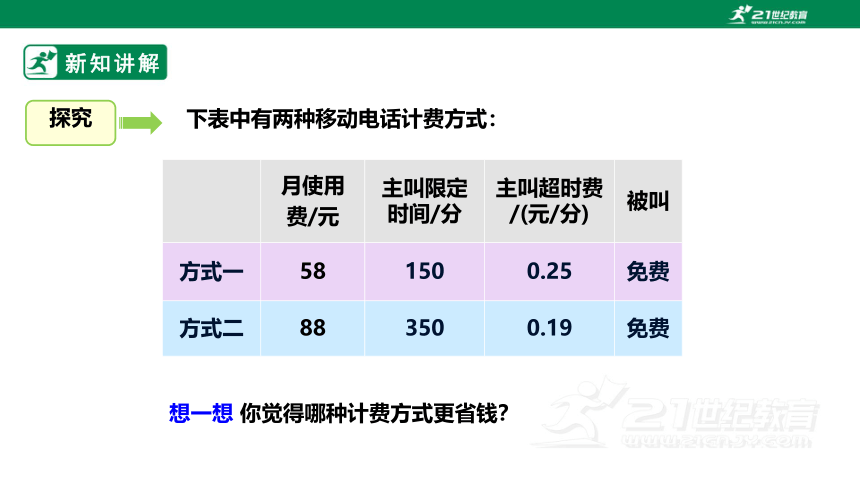
下表中有两种移动电话计费方式:
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费/(元/分)
主叫限定时间/分
月使用
费/元
探究
想一想 你觉得哪种计费方式更省钱?
新知讲解
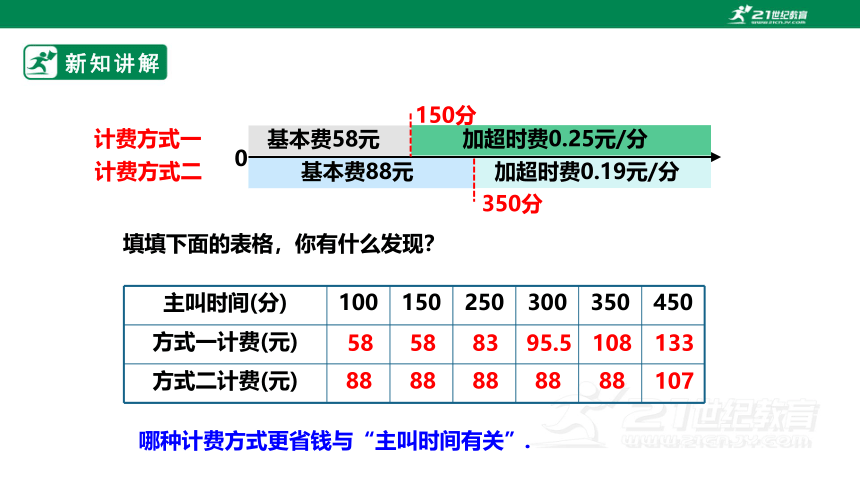
填填下面的表格,你有什么发现?
主叫时间(分) 100 150 250 300 350 450
方式一计费(元)
方式二计费(元)
58
58
83
95.5
108
133
88
88
88
88
88
107
计费方式一
0
加超时费0.19元/分
基本费88元
基本费58元
加超时费0.25元/分
150分
350分
计费方式二
哪种计费方式更省钱与“主叫时间有关”.
新知讲解
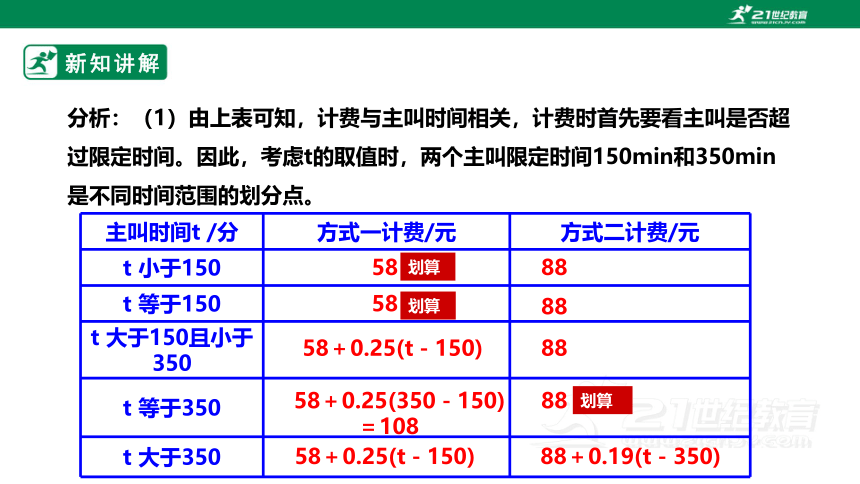
分析:(1)由上表可知,计费与主叫时间相关,计费时首先要看主叫是否超过限定时间。因此,考虑t的取值时,两个主叫限定时间150min和350min是不同时间范围的划分点。
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150
t 等于150
t 大于150且小于 350
t 等于350
t 大于350
58
88
58
88
88
88
58+0.25(t-150)
58+0.25(350-150)
=108
58+0.25(t-150)
88+0.19(t-350)
划算
划算
划算
新知讲解
主叫时间t /分 方式一计费/元 方式二计费/元
t 大于150且小于 350 58+0.25(t-150) 88
依题意得: 58+0.25(t-150) = 88
去括号得: 58+0.25t-37.5 = 88
移项、合并同类项得: 0.25t = 67.5
系数化1得: t =270
∴当 t =270分时,两种计费方式的费用相等,
新知讲解
因此,如果主叫时间恰是270min,按两种方式的计费相等,都是88元;
如果主叫时间大于150min且小于270,按方式一的计费少于按方式二的计费;
如果主叫时间大于270min且小于350min,按方式一的计费多于按方式二的计费。
主叫时间t /分 方式一计费/元 方式二计费/元
t 大于350 58+0.25(t-150) 88+0.19(t-350)
当t >350分时,两种计费方式哪种更合算呢?
新知讲解
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150
t 等于150
t 大于150且小于 350
t 等于350
t 大于350
月使用费/元 主叫限定时间(元/min) 主叫超时费 (元/min) 被叫
方式一 58 150 0.25 免费
方式二 88 350 0.19 免费
58
88
58
88
88
88
58+0.25(t-150)
58+0.25(350-150)
=108
58+0.25(t-150)
88+0.19(t-350)
划算
270
划算
108+0.25(t-350)
新知讲解
加超时费0.19元/分
基本费88元
加超时费0.25元/分
基本费58元
350
0
150
计费方式一
108
88
58
88
( t 是正整数)
t /分
88
88
?
270
综合以上的分析,可以发现:
时,选择方式一省钱;
时,选择方式二省钱.
t 小于 270分
t 大于 270分
课堂练习
1. 小明所在城市的“阶梯水价”收费办法是:每户用水不超过5吨,每吨水费x元;超过5吨,超过部分每吨加收2元,小明家今年5月份用水9吨,共交水费为44元,根据题意列出关于x的方程正确的是( )
A.5x+4(x+2)=44 B.5x+4(x-2)=44
C.9(x+2)=44 D.9(x+2)-4×2=44
A
课堂练习
2.某市出租车起步价是5元(3 km及3 km以内为起步价),以后每千米是1.6元,不足1 km按1 km收费,小明乘出租车到达目的地时计价器显示为11.4元,则此出租车行驶的路程可能是( )
A.5.5 km B.6.9 km C.7.5 km D.8.1 km
3.某服装商店出售一种优惠购物卡,花200元买这种卡后,凭卡可在这家商店按八折购物,下列情况买卡购物合算的是( )
A.购900元 B.购500元
C.购1 200元 D.购1 000元
B
C
课堂练习
4. 某市生活拨号上网有两种收费方式,用户可以任选其一.
A计时制:0.05 元/分钟;B包月制:60 元/月(限一部个人住宅电话上网). 此外,两种上网方式都得加收通信费 0.02 元/分钟.
(1) 某用户某月上网时间为x小时,请分别写出两种收费方式下该用户应该支付的费用;
(2) 你认为采用哪种方式比较合算?
课堂练习
(2) 由 4.2x = 60+1.2x,得 x=20. 又由题意可知,
上网时间越长,采用包月制越合算.
所以,当 0 < x < 20 时,采用计时制合算;
当 x=20 时,两种方式费用相同;
当 x > 20 时,采用包月制合算.
解:(1) 采用计时制:(0.05+0.02)×60x=4.2x,
采用包月制:60+0.02×60x=60+1.2x;
课堂练习
5.为鼓励居民节约用电,某省试行阶梯电价收费制,具体执行方案如下表:
档次 每户每月用电量(度) 执行电价(元/度)
第一档 小于或等于200 0.55
第二档 大于200且小于400 0.6
第三档 大于或等于400 0.85
例如:一户居民七月份用电420度,则需缴电费420×0.85=357(元).某户居民五、六月份共用电500度,缴电费290.5元.已知该用户六月份用电量大于五月份,且五、六月份的用电量均小于400度,则该户居民五、六月份各用电多少度?
课堂练习
解:∵该户居民两个月用电量共为500度,
∴两个月用电量不可能都在第一档.
假设该户居民五月、六月每月用电均超过200度,
500×0.6=300(元),
而300>290.5,不符合题意.
又∵六月份用电量大于五月份,∴五月份用电量在第一档,
假设六月份用电量在第三档,不符合题意,
∴六月份用电量在第二档.
由此,设该户居民五月份用电x度,则六月份用电(500-x)度.
根据题意,得
0.55x+0.6(500-x)=290.5,
解得x=190,
则500-190=310(度).
答:该户居民五月份用电190度,六月份用电310度.
课堂总结
方法
解决电话计费问题需要明确“哪种计费方式更省钱”与“主叫时间”有关.
关键
此类问题的关键是能够根据已知条件找到合适的分段点,然后建立方程模型分类讨论,从而得出整体选择方案.
计费
问题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.4 第3课时
分段计费与方案决策问题
人教版 七年级上册
教学目标
教学目标:
1.掌握应用方程解决实际问题的方法步骤,提高分析问题、解决问题的能力。
2.通过探索球赛积分表中数量关系的过程,进一步体会方程是解决实际问题的数学模型,并且明确用方程解决实际问题时,不仅要注意解方程的过程是否正确,还要检验方程的解是否符合问题的实际意义。
3.鼓励学生自主探究,合作交流,养成自觉反思的良好习惯。
重点:把实际问题转化为数学问题,不仅会列方程求出问题的解,还会进行推理判断.
难点:把实际问题转化为数学问题.
新知导入
我市某县城为鼓励居民节约用水,对自来水用户按分段计费方式收取水费,若每月用水量不超过7 m3,则按每立方米1元收费;若每月用水量超过7 m3,则超过部分按每立方米2元收费.如果某户居民今年5月份缴纳了17元水费,那么这户居民今年5月份的用水量为多少立方米?
解:设5月份用水量为x m3,
则超出7 m3的部分为(x-7)m3.
根据题意,得7×1+(x-7)×2=17,
解得x=12.
答:这户居民今年5月份的用水量为12 m3.
新知讲解
下表中有两种移动电话计费方式:
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费/(元/分)
主叫限定时间/分
月使用
费/元
探究
想一想 你觉得哪种计费方式更省钱?
新知讲解
填填下面的表格,你有什么发现?
主叫时间(分) 100 150 250 300 350 450
方式一计费(元)
方式二计费(元)
58
58
83
95.5
108
133
88
88
88
88
88
107
计费方式一
0
加超时费0.19元/分
基本费88元
基本费58元
加超时费0.25元/分
150分
350分
计费方式二
哪种计费方式更省钱与“主叫时间有关”.
新知讲解
分析:(1)由上表可知,计费与主叫时间相关,计费时首先要看主叫是否超过限定时间。因此,考虑t的取值时,两个主叫限定时间150min和350min是不同时间范围的划分点。
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150
t 等于150
t 大于150且小于 350
t 等于350
t 大于350
58
88
58
88
88
88
58+0.25(t-150)
58+0.25(350-150)
=108
58+0.25(t-150)
88+0.19(t-350)
划算
划算
划算
新知讲解
主叫时间t /分 方式一计费/元 方式二计费/元
t 大于150且小于 350 58+0.25(t-150) 88
依题意得: 58+0.25(t-150) = 88
去括号得: 58+0.25t-37.5 = 88
移项、合并同类项得: 0.25t = 67.5
系数化1得: t =270
∴当 t =270分时,两种计费方式的费用相等,
新知讲解
因此,如果主叫时间恰是270min,按两种方式的计费相等,都是88元;
如果主叫时间大于150min且小于270,按方式一的计费少于按方式二的计费;
如果主叫时间大于270min且小于350min,按方式一的计费多于按方式二的计费。
主叫时间t /分 方式一计费/元 方式二计费/元
t 大于350 58+0.25(t-150) 88+0.19(t-350)
当t >350分时,两种计费方式哪种更合算呢?
新知讲解
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150
t 等于150
t 大于150且小于 350
t 等于350
t 大于350
月使用费/元 主叫限定时间(元/min) 主叫超时费 (元/min) 被叫
方式一 58 150 0.25 免费
方式二 88 350 0.19 免费
58
88
58
88
88
88
58+0.25(t-150)
58+0.25(350-150)
=108
58+0.25(t-150)
88+0.19(t-350)
划算
270
划算
108+0.25(t-350)
新知讲解
加超时费0.19元/分
基本费88元
加超时费0.25元/分
基本费58元
350
0
150
计费方式一
108
88
58
88
( t 是正整数)
t /分
88
88
?
270
综合以上的分析,可以发现:
时,选择方式一省钱;
时,选择方式二省钱.
t 小于 270分
t 大于 270分
课堂练习
1. 小明所在城市的“阶梯水价”收费办法是:每户用水不超过5吨,每吨水费x元;超过5吨,超过部分每吨加收2元,小明家今年5月份用水9吨,共交水费为44元,根据题意列出关于x的方程正确的是( )
A.5x+4(x+2)=44 B.5x+4(x-2)=44
C.9(x+2)=44 D.9(x+2)-4×2=44
A
课堂练习
2.某市出租车起步价是5元(3 km及3 km以内为起步价),以后每千米是1.6元,不足1 km按1 km收费,小明乘出租车到达目的地时计价器显示为11.4元,则此出租车行驶的路程可能是( )
A.5.5 km B.6.9 km C.7.5 km D.8.1 km
3.某服装商店出售一种优惠购物卡,花200元买这种卡后,凭卡可在这家商店按八折购物,下列情况买卡购物合算的是( )
A.购900元 B.购500元
C.购1 200元 D.购1 000元
B
C
课堂练习
4. 某市生活拨号上网有两种收费方式,用户可以任选其一.
A计时制:0.05 元/分钟;B包月制:60 元/月(限一部个人住宅电话上网). 此外,两种上网方式都得加收通信费 0.02 元/分钟.
(1) 某用户某月上网时间为x小时,请分别写出两种收费方式下该用户应该支付的费用;
(2) 你认为采用哪种方式比较合算?
课堂练习
(2) 由 4.2x = 60+1.2x,得 x=20. 又由题意可知,
上网时间越长,采用包月制越合算.
所以,当 0 < x < 20 时,采用计时制合算;
当 x=20 时,两种方式费用相同;
当 x > 20 时,采用包月制合算.
解:(1) 采用计时制:(0.05+0.02)×60x=4.2x,
采用包月制:60+0.02×60x=60+1.2x;
课堂练习
5.为鼓励居民节约用电,某省试行阶梯电价收费制,具体执行方案如下表:
档次 每户每月用电量(度) 执行电价(元/度)
第一档 小于或等于200 0.55
第二档 大于200且小于400 0.6
第三档 大于或等于400 0.85
例如:一户居民七月份用电420度,则需缴电费420×0.85=357(元).某户居民五、六月份共用电500度,缴电费290.5元.已知该用户六月份用电量大于五月份,且五、六月份的用电量均小于400度,则该户居民五、六月份各用电多少度?
课堂练习
解:∵该户居民两个月用电量共为500度,
∴两个月用电量不可能都在第一档.
假设该户居民五月、六月每月用电均超过200度,
500×0.6=300(元),
而300>290.5,不符合题意.
又∵六月份用电量大于五月份,∴五月份用电量在第一档,
假设六月份用电量在第三档,不符合题意,
∴六月份用电量在第二档.
由此,设该户居民五月份用电x度,则六月份用电(500-x)度.
根据题意,得
0.55x+0.6(500-x)=290.5,
解得x=190,
则500-190=310(度).
答:该户居民五月份用电190度,六月份用电310度.
课堂总结
方法
解决电话计费问题需要明确“哪种计费方式更省钱”与“主叫时间”有关.
关键
此类问题的关键是能够根据已知条件找到合适的分段点,然后建立方程模型分类讨论,从而得出整体选择方案.
计费
问题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
