活动单导学课程 苏教版高中数学选择性必修第一册第四章数列4.4.1 数学归纳法(1) 学案(有答案)
文档属性
| 名称 | 活动单导学课程 苏教版高中数学选择性必修第一册第四章数列4.4.1 数学归纳法(1) 学案(有答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 229.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 00:00:00 | ||
图片预览


文档简介
4.4.1 数学归纳法(1)
1. 了解数学归纳法原理,能用数学归纳法证明一些简单的数学命题.
2. 通过数学归纳法的学习,体会用不完全归纳法发现规律,用数学归纳法证明规律的途径.
活动一 了解数学归纳法的背景
情境1:有一种多米诺骨牌游戏,在一个平面上摆一排骨牌(每块骨牌都竖起),假定这排骨牌有无数块,我们要使所有的骨牌都倒下,只要做两件事就行了.第一,使第一块骨牌倒下;第二,保证前一块骨牌倒下后一定能击倒下一块骨牌.
思考1
这个游戏中,能使所有多米诺骨牌全部倒下的条件是什么?
情境2:对于数列{an},已知a1=1,且an+1=(n=1,2,3……),通过对n=1,2,3,4,前4项的归纳,我们可以猜想出其通项公式为an=,但归纳推理得出的猜想不一定成立,必须经过严格的证明.
要证明这个猜想,同学们自然就会想到从n=5开始一个个往下验证,当n较小时可以逐个验证,但当n较大时,逐个验证起来会很麻烦,特别是证明n取所有正整数时,逐个验证是不可能的.故需要寻求一种方法,通过有限个步骤的推理,证明n取所有正整数n都成立.
思考2
你认为证明数列的通项公式是an=这个猜想与上述多米诺骨牌游戏有相似性吗?试类比多米诺骨牌游戏解决这个问题.
活动二 了解数学归纳法的原理
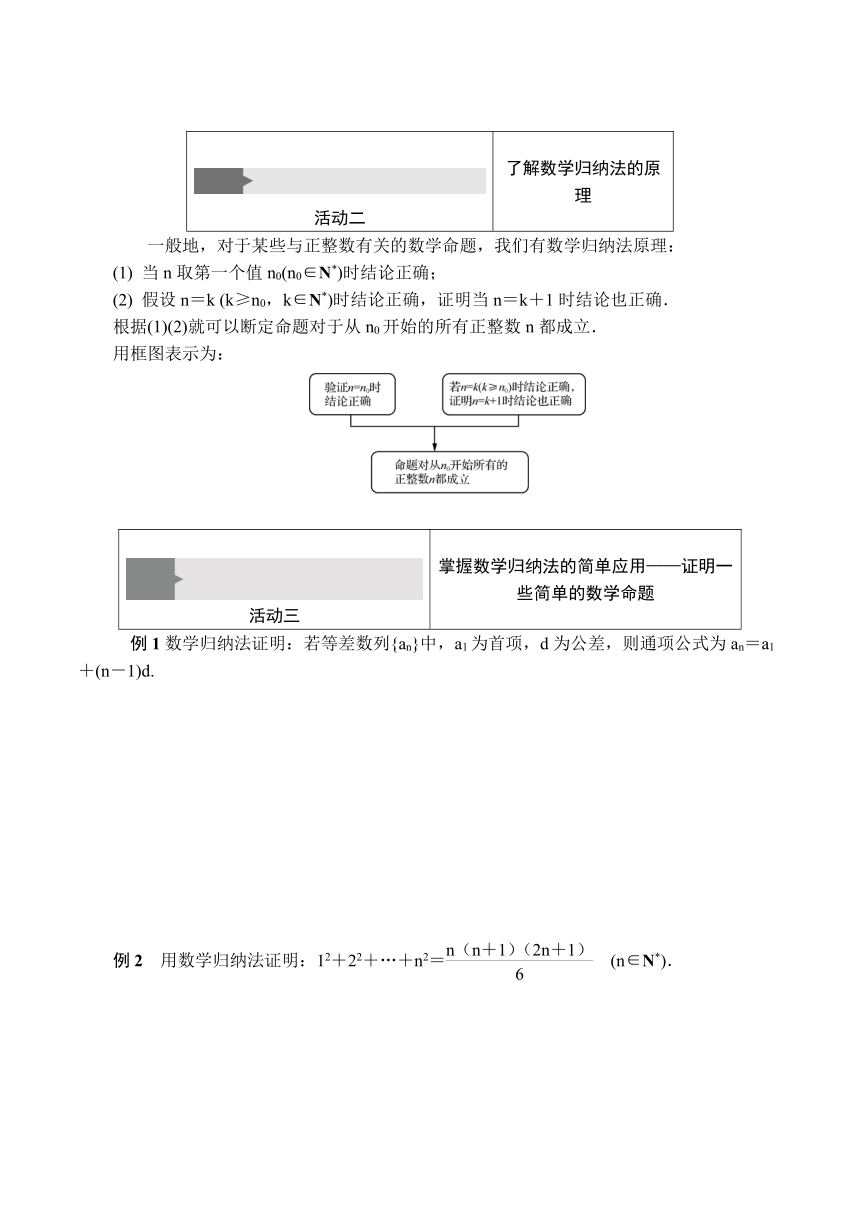
一般地,对于某些与正整数有关的数学命题,我们有数学归纳法原理:
(1) 当n取第一个值n0(n0∈N*)时结论正确;
(2) 假设n=k (k≥n0,k∈N*)时结论正确,证明当n=k+1时结论也正确.
根据(1)(2)就可以断定命题对于从n0开始的所有正整数n都成立.
用框图表示为:
活动三 掌握数学归纳法的简单应用——证明一些简单的数学命题
例1数学归纳法证明:若等差数列{an}中,a1为首项,d为公差,则通项公式为an=a1+(n-1)d.
例2 用数学归纳法证明:12+22+…+n2= (n∈N*).
用数学归纳法证明:当n≥2,n∈N*时,…(1-)=.
活动四 用数学归纳法证明不等式
例3 求证:++…+>(n≥2,n∈N*).
用数学归纳法证明不等式的四个关键:
(1) 验证第一个n的值时,要注意n0不一定为1,若n>k(k为正整数),则n0=k+1;
(2) 证明不等式的第二步中,从n=k到n=k+1的推导过程中,一定要用归纳假设,不运用归纳假设的证明不是数学归纳法,因为缺少归纳假设;
(3) 用数学归纳法证明与n有关的不等式一般有两种具体形式:一是直接给出不等式,按要求进行证明;二是给出两个式子,按要求比较它们的大小.对第二类形式往往要先对n取前k个值的情况分别验证比较,以免出现判断失误,最后猜出从某个k值开始都成立的结论,常用数学归纳法证明;
(4) 用数学归纳法证明不等式的关键是由n=k时成立,得n=k+1时成立,主要方法有比较法、放缩法等.
1. 若f(n)=1+++…+(n∈N*),则n=1时,f(n)等于( )
A. 1 B.
C. 1++ D. 以上答案均不正确
2. 已知n∈N?,用数学归纳法证明f(n)=1+4+7+…+(3n-2)=时,假设当n=k(k∈N*)时命题成立,证明当n=k+1时命题也成立,需要用到的f(k+1)与f(k)之间的关系式是( )
A. f(k+1)=f(k)+3k-5 B. f(k+1)=f(k)+3k-2
C. f(k+1)=f(k)+3k+1 D. f(k+1)=f(k)+3k+4
3. (多选)已知一个命题F(k),k=2n(n∈N*),当n=1,2,…,999时,F(k)成立,并且当n=999+1时,它也成立,则下列命题中不正确的是( )
A. F(k)对于k=2 002成立 B. F(k)对于每一个自然数k成立
C. F(k)对于每一个偶数k成立 D. F(k)对于某些偶数可能不成立
4. 用数学归纳法证明1+2+3+…+2n=n(2n+1)时,从n=k推证n=k+1时,左边增加的代数式是________.
5. 用数学归纳法证明:1+2+3+…+(n+3)=(n∈N*).
参考答案与解析
【活动方案】
思考1:①第一张骨牌倒下;
②任意相邻的两张骨牌,前一张倒下一定导致后一张倒下.
思考2:相似.
①易知,当n=1时,猜想成立;
②假设当n=k,k∈N*时,猜想成立,即ak=,
则当n=k+1时,ak+1===,
即n=k+1时,猜想也成立.
综合①②知,猜想成立.
例1 ①当n=1时,a1=a1+0×d=a1,结论成立;
②假设当n=k时,结论成立,即ak=a1+(k-1)d.
当n=k+1时,ak+1=ak+d=a1+(k-1)d+d=a1+[(k+1)-1]d,
所以当n=k+1时,结论也成立.
综上,an=a1+(n-1)d,对任意n∈N*都成立.
例2 ①当n=1时,12==1,结论成立;
②假设当n=k(k≥1,k∈N*)时,结论也成立,
即12+22+…+k2=.
则当n=k+1时,
12+22+…+k2+(k+1)2
=+(k+1)2
=
=
=,
所以当n=k+1时,结论也成立.
综上,对任意n∈N*,等式都成立.
跟踪训练 ①当n=2时,左边=1-=,右边==,所以n=2时等式成立;
②假设当n=k(k≥2,k∈N*)时等式成立,
即…(1-)=,
则当n=k+1时,
…
=·
===,
所以当n=k+1时,等式也成立.
综上,对任意n≥2,n∈N*,等式都成立.
例3 ①当n=2时,左边=+++=,故左边>右边,不等式成立;
②假设当n=k(k≥2,k∈N*)时,不等式成立,即++…+>,
则当n=k+1时,++…++++
=++…++(++-)>+(++-).
要证++-≥0,
只需证(3k+2)(3k+3)+(3k+1)(3k+3)+(3k+1)(3k+2)-3(3k+1)(3k+2)≥0,
只需证(9k2+15k+6)+(9k2+12k+3)+(9k2+9k+2)-(27k2+27k+6)≥0,
只需证9k+5≥0,显然成立,
所以当n=k+1时,不等式也成立.
综上,对任意n≥2,n∈N*,不等式都成立.
【检测反馈】
1. C
2. C 解析:由题意,得当n=k时,f(k)=1+4+7+…+(3k-2).当n=k+1时,f(k+1)=1+4+7+…+(3k-2)+[3(k+1)-2],则f(k+1)=f(k)+3k+1.
3. ABC 解析:由于命题F(k),k=2n(n∈N*),当n=1,2,…,999时,F(k)成立,并且当n=999+1时,它也成立,可得F(k)对于1~2 000内的偶数均成立,而对于其他数不一定成立,故F(k)对于k=2 002不一定成立,F(k)对于每一个自然数k不一定成立,F(k)对于每一个偶数k不一定成立,F(k)对于某些偶数可能不成立.故选ABC.
4. 4k+3 解析:由题意,可得当n=1时,等式左边=1+2;当n=k时,等式左边=1+2+3+…+2k;当n=k+1时,等式左边=1+2+3+…+2k+(2k+1)+2(k+1),所以从k到k+1时,左边需增加的代数式是(2k+1)+2(k+1)=4k+3.
5. ①当n=1时,左边=1+2+3+4=10,右边==10,等式成立.
②假设n=k(k∈N*)时等式成立,即1+2+3+…+(k+3)=,
那么当n=k+1时,1+2+3+…+(k+3)+(k+4)=+(k+4)=,
即当n=k+1时,等式成立.
综上,1+2+3+…+(n+3)=(n∈N*)成立.
1. 了解数学归纳法原理,能用数学归纳法证明一些简单的数学命题.
2. 通过数学归纳法的学习,体会用不完全归纳法发现规律,用数学归纳法证明规律的途径.
活动一 了解数学归纳法的背景
情境1:有一种多米诺骨牌游戏,在一个平面上摆一排骨牌(每块骨牌都竖起),假定这排骨牌有无数块,我们要使所有的骨牌都倒下,只要做两件事就行了.第一,使第一块骨牌倒下;第二,保证前一块骨牌倒下后一定能击倒下一块骨牌.
思考1
这个游戏中,能使所有多米诺骨牌全部倒下的条件是什么?
情境2:对于数列{an},已知a1=1,且an+1=(n=1,2,3……),通过对n=1,2,3,4,前4项的归纳,我们可以猜想出其通项公式为an=,但归纳推理得出的猜想不一定成立,必须经过严格的证明.
要证明这个猜想,同学们自然就会想到从n=5开始一个个往下验证,当n较小时可以逐个验证,但当n较大时,逐个验证起来会很麻烦,特别是证明n取所有正整数时,逐个验证是不可能的.故需要寻求一种方法,通过有限个步骤的推理,证明n取所有正整数n都成立.
思考2
你认为证明数列的通项公式是an=这个猜想与上述多米诺骨牌游戏有相似性吗?试类比多米诺骨牌游戏解决这个问题.
活动二 了解数学归纳法的原理
一般地,对于某些与正整数有关的数学命题,我们有数学归纳法原理:
(1) 当n取第一个值n0(n0∈N*)时结论正确;
(2) 假设n=k (k≥n0,k∈N*)时结论正确,证明当n=k+1时结论也正确.
根据(1)(2)就可以断定命题对于从n0开始的所有正整数n都成立.
用框图表示为:
活动三 掌握数学归纳法的简单应用——证明一些简单的数学命题
例1数学归纳法证明:若等差数列{an}中,a1为首项,d为公差,则通项公式为an=a1+(n-1)d.
例2 用数学归纳法证明:12+22+…+n2= (n∈N*).
用数学归纳法证明:当n≥2,n∈N*时,…(1-)=.
活动四 用数学归纳法证明不等式
例3 求证:++…+>(n≥2,n∈N*).
用数学归纳法证明不等式的四个关键:
(1) 验证第一个n的值时,要注意n0不一定为1,若n>k(k为正整数),则n0=k+1;
(2) 证明不等式的第二步中,从n=k到n=k+1的推导过程中,一定要用归纳假设,不运用归纳假设的证明不是数学归纳法,因为缺少归纳假设;
(3) 用数学归纳法证明与n有关的不等式一般有两种具体形式:一是直接给出不等式,按要求进行证明;二是给出两个式子,按要求比较它们的大小.对第二类形式往往要先对n取前k个值的情况分别验证比较,以免出现判断失误,最后猜出从某个k值开始都成立的结论,常用数学归纳法证明;
(4) 用数学归纳法证明不等式的关键是由n=k时成立,得n=k+1时成立,主要方法有比较法、放缩法等.
1. 若f(n)=1+++…+(n∈N*),则n=1时,f(n)等于( )
A. 1 B.
C. 1++ D. 以上答案均不正确
2. 已知n∈N?,用数学归纳法证明f(n)=1+4+7+…+(3n-2)=时,假设当n=k(k∈N*)时命题成立,证明当n=k+1时命题也成立,需要用到的f(k+1)与f(k)之间的关系式是( )
A. f(k+1)=f(k)+3k-5 B. f(k+1)=f(k)+3k-2
C. f(k+1)=f(k)+3k+1 D. f(k+1)=f(k)+3k+4
3. (多选)已知一个命题F(k),k=2n(n∈N*),当n=1,2,…,999时,F(k)成立,并且当n=999+1时,它也成立,则下列命题中不正确的是( )
A. F(k)对于k=2 002成立 B. F(k)对于每一个自然数k成立
C. F(k)对于每一个偶数k成立 D. F(k)对于某些偶数可能不成立
4. 用数学归纳法证明1+2+3+…+2n=n(2n+1)时,从n=k推证n=k+1时,左边增加的代数式是________.
5. 用数学归纳法证明:1+2+3+…+(n+3)=(n∈N*).
参考答案与解析
【活动方案】
思考1:①第一张骨牌倒下;
②任意相邻的两张骨牌,前一张倒下一定导致后一张倒下.
思考2:相似.
①易知,当n=1时,猜想成立;
②假设当n=k,k∈N*时,猜想成立,即ak=,
则当n=k+1时,ak+1===,
即n=k+1时,猜想也成立.
综合①②知,猜想成立.
例1 ①当n=1时,a1=a1+0×d=a1,结论成立;
②假设当n=k时,结论成立,即ak=a1+(k-1)d.
当n=k+1时,ak+1=ak+d=a1+(k-1)d+d=a1+[(k+1)-1]d,
所以当n=k+1时,结论也成立.
综上,an=a1+(n-1)d,对任意n∈N*都成立.
例2 ①当n=1时,12==1,结论成立;
②假设当n=k(k≥1,k∈N*)时,结论也成立,
即12+22+…+k2=.
则当n=k+1时,
12+22+…+k2+(k+1)2
=+(k+1)2
=
=
=,
所以当n=k+1时,结论也成立.
综上,对任意n∈N*,等式都成立.
跟踪训练 ①当n=2时,左边=1-=,右边==,所以n=2时等式成立;
②假设当n=k(k≥2,k∈N*)时等式成立,
即…(1-)=,
则当n=k+1时,
…
=·
===,
所以当n=k+1时,等式也成立.
综上,对任意n≥2,n∈N*,等式都成立.
例3 ①当n=2时,左边=+++=,故左边>右边,不等式成立;
②假设当n=k(k≥2,k∈N*)时,不等式成立,即++…+>,
则当n=k+1时,++…++++
=++…++(++-)>+(++-).
要证++-≥0,
只需证(3k+2)(3k+3)+(3k+1)(3k+3)+(3k+1)(3k+2)-3(3k+1)(3k+2)≥0,
只需证(9k2+15k+6)+(9k2+12k+3)+(9k2+9k+2)-(27k2+27k+6)≥0,
只需证9k+5≥0,显然成立,
所以当n=k+1时,不等式也成立.
综上,对任意n≥2,n∈N*,不等式都成立.
【检测反馈】
1. C
2. C 解析:由题意,得当n=k时,f(k)=1+4+7+…+(3k-2).当n=k+1时,f(k+1)=1+4+7+…+(3k-2)+[3(k+1)-2],则f(k+1)=f(k)+3k+1.
3. ABC 解析:由于命题F(k),k=2n(n∈N*),当n=1,2,…,999时,F(k)成立,并且当n=999+1时,它也成立,可得F(k)对于1~2 000内的偶数均成立,而对于其他数不一定成立,故F(k)对于k=2 002不一定成立,F(k)对于每一个自然数k不一定成立,F(k)对于每一个偶数k不一定成立,F(k)对于某些偶数可能不成立.故选ABC.
4. 4k+3 解析:由题意,可得当n=1时,等式左边=1+2;当n=k时,等式左边=1+2+3+…+2k;当n=k+1时,等式左边=1+2+3+…+2k+(2k+1)+2(k+1),所以从k到k+1时,左边需增加的代数式是(2k+1)+2(k+1)=4k+3.
5. ①当n=1时,左边=1+2+3+4=10,右边==10,等式成立.
②假设n=k(k∈N*)时等式成立,即1+2+3+…+(k+3)=,
那么当n=k+1时,1+2+3+…+(k+3)+(k+4)=+(k+4)=,
即当n=k+1时,等式成立.
综上,1+2+3+…+(n+3)=(n∈N*)成立.
