人教版八年级数学上册13.2.2 用坐标表示轴对称 同步练习(含答案)
文档属性
| 名称 | 人教版八年级数学上册13.2.2 用坐标表示轴对称 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 167.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-13 15:22:43 | ||
图片预览


文档简介
13.2.2 用坐标表示轴对称
一.选择题
1.点P(-2,3)关于x轴对称的点的坐标是( )
A.(-2,3) B.(-3,2)
C.(-2,-3) D.(2,3)
2. 在平面直角坐标系中,已知点A(1,2),则点A关于y轴对称的点的坐标为( )
A.(-1,2) B.(1,-2)
C.(2,1) D.(-1,-2)
3. 点(4,-3)关于x轴对称的点的坐标在( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
4. 若点P(5,-6)和点Q(a-1,b+2)关于x轴对称,则a,b的值为( )
A.a=6,b=4 B.a=-6,b=4
C.a=6,b=-4 D.a=-6,b=-4
5.如图,在平面直角坐标系中,△ABC的顶点都在格点上,如果将△ABC先沿y轴翻折,再向上平移3个单位长度,得到△A'B'C',那么点B的对应点B'的坐标为( )
A.(1,7) B.(0,5) C.(3,4) D.(-3,2)
二.填空题
1.已知点P(a,3),Q(-2,b)关于x轴对称,则a=_______,b=_______.
2.点M(-2,1)关于y轴对称的点N的坐标是______,直线MN与y轴的位置关系是________.
3. 如图,△ABO是关于y轴对称的轴对称图形,点A的坐标为(-2,3),则点B的坐标为 .
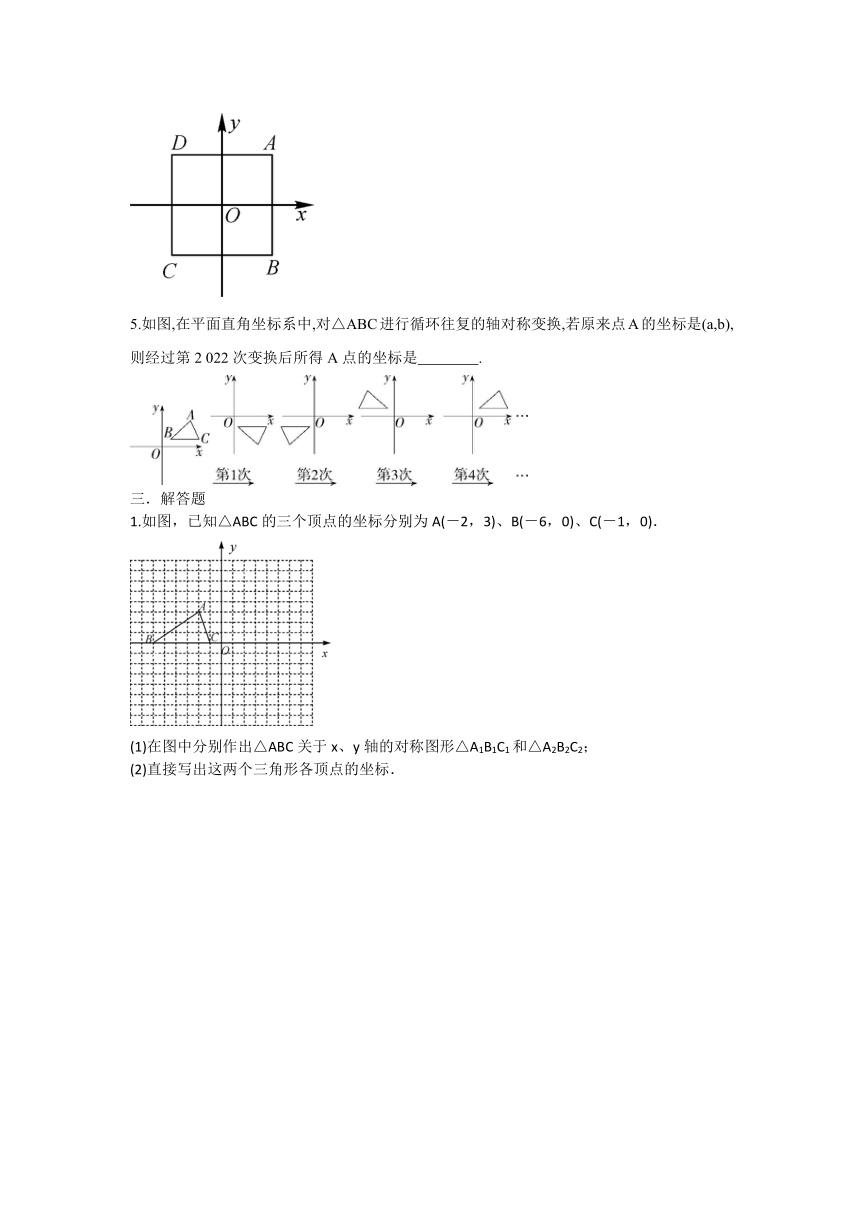
4.已知正方形ABCD在坐标轴上的位置如图所示,x轴、y轴分别是正方形的两条对称轴,若A(2,2),则B点的坐标为________,C点的坐标为_______,D点的坐标为_______.2-1-c-n-j-y
5.如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A的坐标是(a,b),则经过第2 022次变换后所得A点的坐标是 .
解答题
1.如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
(1)在图中分别作出△ABC关于x、y轴的对称图形△A1B1C1和△A2B2C2;
(2)直接写出这两个三角形各顶点的坐标.
2.如图,已知A(2,3),B(3,1),C(-2,-2).
(1)利用关于坐标轴对称的点的坐标的特点,在坐标系中作出△ABC关于y轴对称的图形△A1B1C1,并写出△A1B1C1各个顶点的坐标;
(2)求出△ABC的面积.
3.已知点A(2a-b,5+a),B(2b-1,-a+b).
(1)若点A,B关于x轴对称,求a,b的值;
(2)若点A,B关于y轴对称,求(4a+b)2022的值.
13.2.2 用坐标表示轴对称
参考答案
一.选择题
1.点P(-2,3)关于x轴对称的点的坐标是( C )
A.(-2,3) B.(-3,2)
C.(-2,-3) D.(2,3)
2. 在平面直角坐标系中,已知点A(1,2),则点A关于y轴对称的点的坐标为( A )
A.(-1,2) B.(1,-2)
C.(2,1) D.(-1,-2)
3. 点(4,-3)关于x轴对称的点的坐标在( A )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
4. 若点P(5,-6)和点Q(a-1,b+2)关于x轴对称,则a,b的值为( A )
A.a=6,b=4 B.a=-6,b=4
C.a=6,b=-4 D.a=-6,b=-4
5.如图,在平面直角坐标系中,△ABC的顶点都在格点上,如果将△ABC先沿y轴翻折,再向上平移3个单位长度,得到△A'B'C',那么点B的对应点B'的坐标为( C )
A.(1,7) B.(0,5) C.(3,4) D.(-3,2)
二.填空题
1.已知点P(a,3),Q(-2,b)关于x轴对称,则a=____-2____,b=___-3_____.
2.点M(-2,1)关于y轴对称的点N的坐标是__(2,1)______,直线MN与y轴的位置关系是___垂直_____.
3. 如图,△ABO是关于y轴对称的轴对称图形,点A的坐标为(-2,3),则点B的坐标为 (2,3).
4.已知正方形ABCD在坐标轴上的位置如图所示,x轴、y轴分别是正方形的两条对称轴,若A(2,2),则B点的坐标为__(2,-2)______,C点的坐标为____(-2,-2) ____,D点的坐标为___(-2,2)_____.2-1-c-n-j-y
5.如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A的坐标是(a,b),则经过第2 022次变换后所得A点的坐标是 (-a,-b) .
解答题
1.如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
(1)在图中分别作出△ABC关于x、y轴的对称图形△A1B1C1和△A2B2C2;
(2)直接写出这两个三角形各顶点的坐标.
解(1)图略.(2)A1(-2,-3),B1(-6,0),C1(-1,0),A2(2,3),B2(6,0),C2(1,0).
2.如图,已知A(2,3),B(3,1),C(-2,-2).
(1)利用关于坐标轴对称的点的坐标的特点,在坐标系中作出△ABC关于y轴对称的图形△A1B1C1,并写出△A1B1C1各个顶点的坐标;
(2)求出△ABC的面积.
解:(1)图略,
A1(-2,3),
B1(-3,1),
C1(2,-2).
(2)S△ABC=5×5-×3×5-×1×2-×5×4=.
3.已知点A(2a-b,5+a),B(2b-1,-a+b).
(1)若点A,B关于x轴对称,求a,b的值;
(2)若点A,B关于y轴对称,求(4a+b)2022的值.
解:(1)∵点A,B关于x轴对称,
∴
解得
(2)∵点A,B关于y轴对称,
∴
解得
∴(4a+b)2022=[4×(-1)+3]2022=1.
一.选择题
1.点P(-2,3)关于x轴对称的点的坐标是( )
A.(-2,3) B.(-3,2)
C.(-2,-3) D.(2,3)
2. 在平面直角坐标系中,已知点A(1,2),则点A关于y轴对称的点的坐标为( )
A.(-1,2) B.(1,-2)
C.(2,1) D.(-1,-2)
3. 点(4,-3)关于x轴对称的点的坐标在( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
4. 若点P(5,-6)和点Q(a-1,b+2)关于x轴对称,则a,b的值为( )
A.a=6,b=4 B.a=-6,b=4
C.a=6,b=-4 D.a=-6,b=-4
5.如图,在平面直角坐标系中,△ABC的顶点都在格点上,如果将△ABC先沿y轴翻折,再向上平移3个单位长度,得到△A'B'C',那么点B的对应点B'的坐标为( )
A.(1,7) B.(0,5) C.(3,4) D.(-3,2)
二.填空题
1.已知点P(a,3),Q(-2,b)关于x轴对称,则a=_______,b=_______.
2.点M(-2,1)关于y轴对称的点N的坐标是______,直线MN与y轴的位置关系是________.
3. 如图,△ABO是关于y轴对称的轴对称图形,点A的坐标为(-2,3),则点B的坐标为 .
4.已知正方形ABCD在坐标轴上的位置如图所示,x轴、y轴分别是正方形的两条对称轴,若A(2,2),则B点的坐标为________,C点的坐标为_______,D点的坐标为_______.2-1-c-n-j-y
5.如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A的坐标是(a,b),则经过第2 022次变换后所得A点的坐标是 .
解答题
1.如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
(1)在图中分别作出△ABC关于x、y轴的对称图形△A1B1C1和△A2B2C2;
(2)直接写出这两个三角形各顶点的坐标.
2.如图,已知A(2,3),B(3,1),C(-2,-2).
(1)利用关于坐标轴对称的点的坐标的特点,在坐标系中作出△ABC关于y轴对称的图形△A1B1C1,并写出△A1B1C1各个顶点的坐标;
(2)求出△ABC的面积.
3.已知点A(2a-b,5+a),B(2b-1,-a+b).
(1)若点A,B关于x轴对称,求a,b的值;
(2)若点A,B关于y轴对称,求(4a+b)2022的值.
13.2.2 用坐标表示轴对称
参考答案
一.选择题
1.点P(-2,3)关于x轴对称的点的坐标是( C )
A.(-2,3) B.(-3,2)
C.(-2,-3) D.(2,3)
2. 在平面直角坐标系中,已知点A(1,2),则点A关于y轴对称的点的坐标为( A )
A.(-1,2) B.(1,-2)
C.(2,1) D.(-1,-2)
3. 点(4,-3)关于x轴对称的点的坐标在( A )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
4. 若点P(5,-6)和点Q(a-1,b+2)关于x轴对称,则a,b的值为( A )
A.a=6,b=4 B.a=-6,b=4
C.a=6,b=-4 D.a=-6,b=-4
5.如图,在平面直角坐标系中,△ABC的顶点都在格点上,如果将△ABC先沿y轴翻折,再向上平移3个单位长度,得到△A'B'C',那么点B的对应点B'的坐标为( C )
A.(1,7) B.(0,5) C.(3,4) D.(-3,2)
二.填空题
1.已知点P(a,3),Q(-2,b)关于x轴对称,则a=____-2____,b=___-3_____.
2.点M(-2,1)关于y轴对称的点N的坐标是__(2,1)______,直线MN与y轴的位置关系是___垂直_____.
3. 如图,△ABO是关于y轴对称的轴对称图形,点A的坐标为(-2,3),则点B的坐标为 (2,3).
4.已知正方形ABCD在坐标轴上的位置如图所示,x轴、y轴分别是正方形的两条对称轴,若A(2,2),则B点的坐标为__(2,-2)______,C点的坐标为____(-2,-2) ____,D点的坐标为___(-2,2)_____.2-1-c-n-j-y
5.如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A的坐标是(a,b),则经过第2 022次变换后所得A点的坐标是 (-a,-b) .
解答题
1.如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
(1)在图中分别作出△ABC关于x、y轴的对称图形△A1B1C1和△A2B2C2;
(2)直接写出这两个三角形各顶点的坐标.
解(1)图略.(2)A1(-2,-3),B1(-6,0),C1(-1,0),A2(2,3),B2(6,0),C2(1,0).
2.如图,已知A(2,3),B(3,1),C(-2,-2).
(1)利用关于坐标轴对称的点的坐标的特点,在坐标系中作出△ABC关于y轴对称的图形△A1B1C1,并写出△A1B1C1各个顶点的坐标;
(2)求出△ABC的面积.
解:(1)图略,
A1(-2,3),
B1(-3,1),
C1(2,-2).
(2)S△ABC=5×5-×3×5-×1×2-×5×4=.
3.已知点A(2a-b,5+a),B(2b-1,-a+b).
(1)若点A,B关于x轴对称,求a,b的值;
(2)若点A,B关于y轴对称,求(4a+b)2022的值.
解:(1)∵点A,B关于x轴对称,
∴
解得
(2)∵点A,B关于y轴对称,
∴
解得
∴(4a+b)2022=[4×(-1)+3]2022=1.
