人教版八年级数学上册13.3.2.2含30°角的直角三角形的性质 同步练习(含答案)
文档属性
| 名称 | 人教版八年级数学上册13.3.2.2含30°角的直角三角形的性质 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 61.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-13 15:23:17 | ||
图片预览


文档简介
13.3.2.2 含30°角的直角三角形的性质
一.选择题
1.有一直角三角板,30°角所对直角边长是6 cm,则斜边的长是( )
A.3 cm B.6 cm
C.10 cm D.12 cm
2.△ABC中,∠A∶∠B∶∠C=1∶2∶3,则BC∶AB等于( )
A.2∶1 B.1∶2
C.1∶3 D.2∶3
3.Rt△ABC中,CD是斜边AB上的高,∠B=30°,AD=2 cm,则AB的长度是( )
A.2 cm B.4 cm
C.8 cm D.16 cm
4. 如图,在等边三角形ABC中,AB=10 cm,D是AB的中点,过点D作DE⊥AC于点E,则AE的长是( )
A.2.5 cm B.5 cm
C.7 cm D.7.5 cm
5. 如图,在Rt△ABC中,∠C=90°,∠A=30°,AB+BC=9 cm,则AB的长为( )
A. 3 cm B. 4 cm
C. 5 cm D. 6 cm
二.填空题
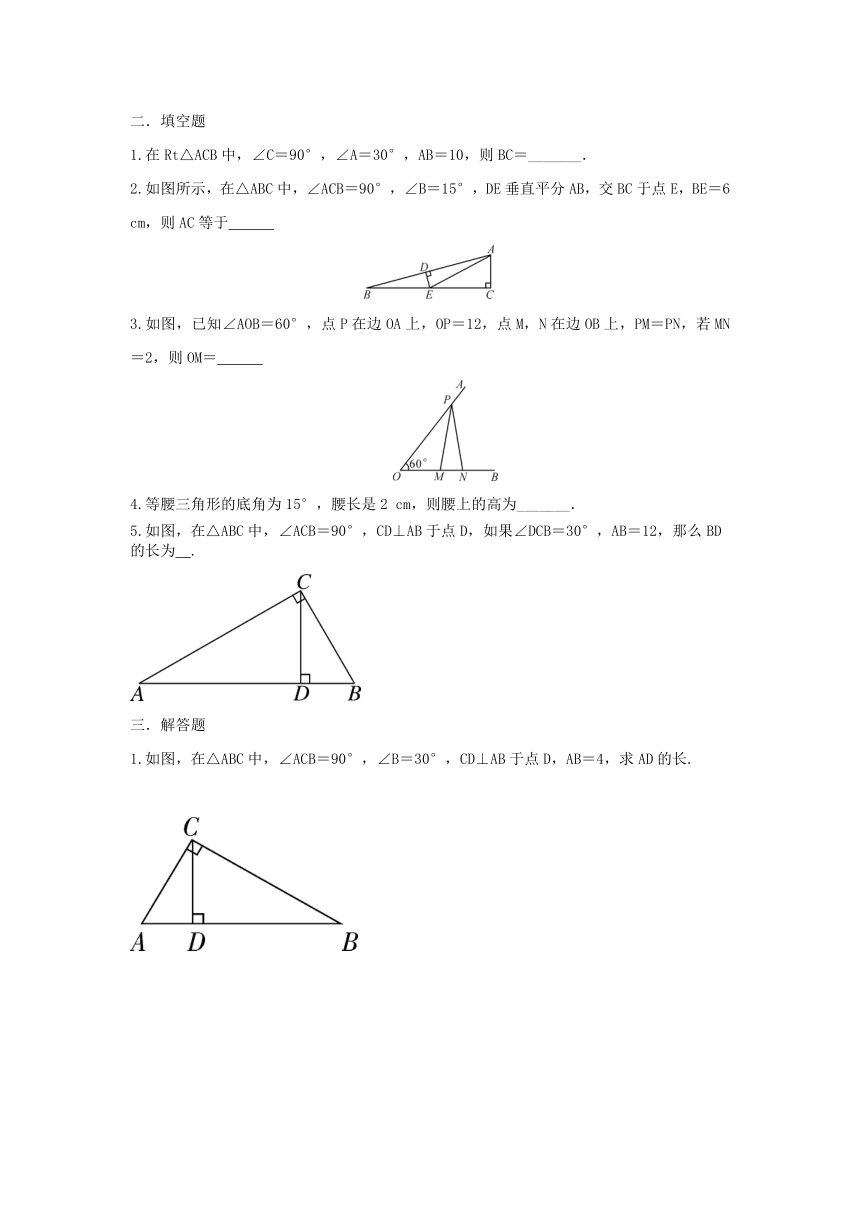
1.在Rt△ACB中,∠C=90°,∠A=30°,AB=10,则BC=_______.
2.如图所示,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,BE=6 cm,则AC等于
3.如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=
4.等腰三角形的底角为15°,腰长是2 cm,则腰上的高为_______.
5.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,如果∠DCB=30°,AB=12,那么BD的长为 .
解答题
1.如图,在△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于点D,AB=4,求AD的长.
2. 如图,在Rt△ABC中,∠C=90°,∠B=15°,DE垂直平分AB交BC于点E,BE=4,求AC的长.
3. 如图,在△ABC中,AB=AC,∠BAC=120°,D为BC的中点,DE⊥AC于点E,AE=8,求CE的长.
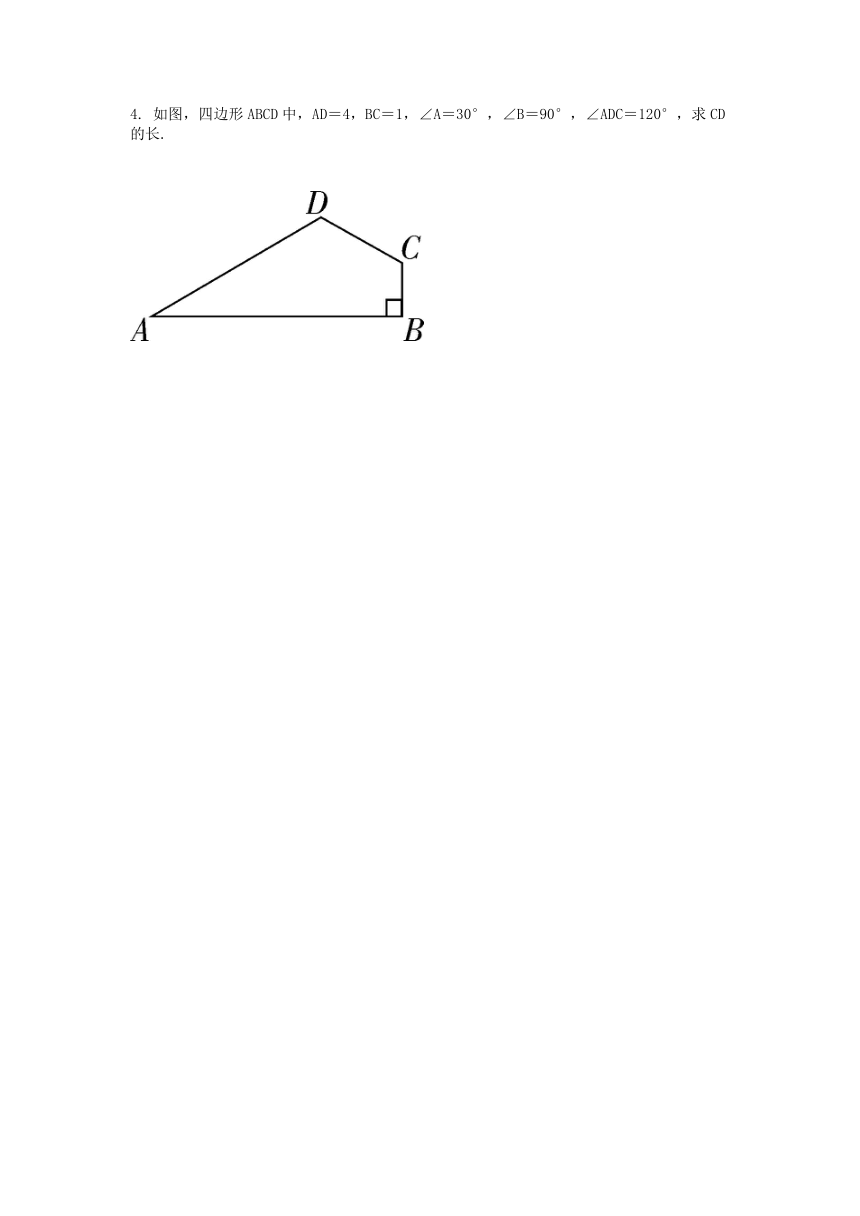
4. 如图,四边形ABCD中,AD=4,BC=1,∠A=30°,∠B=90°,∠ADC=120°,求CD的长.
13.3.2.2 含30°角的直角三角形的性质
参考答案
一.选择题
1.有一直角三角板,30°角所对直角边长是6 cm,则斜边的长是( D )
A.3 cm B.6 cm
C.10 cm D.12 cm
2.△ABC中,∠A∶∠B∶∠C=1∶2∶3,则BC∶AB等于( B )
A.2∶1 B.1∶2
C.1∶3 D.2∶3
3.Rt△ABC中,CD是斜边AB上的高,∠B=30°,AD=2 cm,则AB的长度是( C )
A.2 cm B.4 cm
C.8 cm D.16 cm
4. 如图,在等边三角形ABC中,AB=10 cm,D是AB的中点,过点D作DE⊥AC于点E,则AE的长是( A )
A.2.5 cm B.5 cm
C.7 cm D.7.5 cm
5. 如图,在Rt△ABC中,∠C=90°,∠A=30°,AB+BC=9 cm,则AB的长为( D )
A. 3 cm B. 4 cm
C. 5 cm D. 6 cm
二.填空题
1.在Rt△ACB中,∠C=90°,∠A=30°,AB=10,则BC=___5_____.
2.如图所示,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,BE=6 cm,则AC等于 3cm
3.如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM= 5
4.等腰三角形的底角为15°,腰长是2 cm,则腰上的高为_____1cm___.
5.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,如果∠DCB=30°,AB=12,那么BD的长为 3 .
解答题
1.如图,在△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于点D,AB=4,求AD的长.
解:∵∠ACB=90°,∠B=30°,
∴AC=AB=2.
∵∠ACB=90°,
∴∠ACD+∠BCD=90°.
∵CD⊥AB,
∴∠B+∠BCD=90°.
∴∠ACD=∠B=30°.
∴AD=AC=1.
2. 如图,在Rt△ABC中,∠C=90°,∠B=15°,DE垂直平分AB交BC于点E,BE=4,求AC的长.
解:∵DE垂直平分AB,
∴AE=BE=4.
∴∠BAE=∠B=15°.∴∠AEC=∠BAE+∠B=15°+15°=30°.
∵∠C=90°,∴AC=AE=×4=2.
3. 如图,在△ABC中,AB=AC,∠BAC=120°,D为BC的中点,DE⊥AC于点E,AE=8,求CE的长.
解:连接AD.
∵AB=AC,∠BAC=120°,D为BC的中点,
∴AD⊥BC,AD平分∠BAC,∠B=∠C=30°.
∴∠DAC=∠BAC=60°.
∵DE⊥AC于点E,∴∠AED=90°.
∴∠ADE=30°.
在Rt△ADE中,AE=8,∠ADE=30°,
∴AD=2AE=16.
在Rt△ADC中,AD=16,∠C=30°,
∴AC=2AD=32.
∴CE=AC-AE=32-8=24.
4. 如图,四边形ABCD中,AD=4,BC=1,∠A=30°,∠B=90°,∠ADC=120°,求CD的长.
解:延长AD,BC交于点E.
∵∠A=30°,∠B=90°,
∴∠E=60°.
∵∠ADC=120°,
∴∠EDC=60°.
∴△EDC是等边三角形.
设CD=CE=DE=x,∵AD=4,BC=1,
∴2(1+x)=x+4.解得x=2.∴CD=2.
一.选择题
1.有一直角三角板,30°角所对直角边长是6 cm,则斜边的长是( )
A.3 cm B.6 cm
C.10 cm D.12 cm
2.△ABC中,∠A∶∠B∶∠C=1∶2∶3,则BC∶AB等于( )
A.2∶1 B.1∶2
C.1∶3 D.2∶3
3.Rt△ABC中,CD是斜边AB上的高,∠B=30°,AD=2 cm,则AB的长度是( )
A.2 cm B.4 cm
C.8 cm D.16 cm
4. 如图,在等边三角形ABC中,AB=10 cm,D是AB的中点,过点D作DE⊥AC于点E,则AE的长是( )
A.2.5 cm B.5 cm
C.7 cm D.7.5 cm
5. 如图,在Rt△ABC中,∠C=90°,∠A=30°,AB+BC=9 cm,则AB的长为( )
A. 3 cm B. 4 cm
C. 5 cm D. 6 cm
二.填空题
1.在Rt△ACB中,∠C=90°,∠A=30°,AB=10,则BC=_______.
2.如图所示,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,BE=6 cm,则AC等于
3.如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=
4.等腰三角形的底角为15°,腰长是2 cm,则腰上的高为_______.
5.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,如果∠DCB=30°,AB=12,那么BD的长为 .
解答题
1.如图,在△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于点D,AB=4,求AD的长.
2. 如图,在Rt△ABC中,∠C=90°,∠B=15°,DE垂直平分AB交BC于点E,BE=4,求AC的长.
3. 如图,在△ABC中,AB=AC,∠BAC=120°,D为BC的中点,DE⊥AC于点E,AE=8,求CE的长.
4. 如图,四边形ABCD中,AD=4,BC=1,∠A=30°,∠B=90°,∠ADC=120°,求CD的长.
13.3.2.2 含30°角的直角三角形的性质
参考答案
一.选择题
1.有一直角三角板,30°角所对直角边长是6 cm,则斜边的长是( D )
A.3 cm B.6 cm
C.10 cm D.12 cm
2.△ABC中,∠A∶∠B∶∠C=1∶2∶3,则BC∶AB等于( B )
A.2∶1 B.1∶2
C.1∶3 D.2∶3
3.Rt△ABC中,CD是斜边AB上的高,∠B=30°,AD=2 cm,则AB的长度是( C )
A.2 cm B.4 cm
C.8 cm D.16 cm
4. 如图,在等边三角形ABC中,AB=10 cm,D是AB的中点,过点D作DE⊥AC于点E,则AE的长是( A )
A.2.5 cm B.5 cm
C.7 cm D.7.5 cm
5. 如图,在Rt△ABC中,∠C=90°,∠A=30°,AB+BC=9 cm,则AB的长为( D )
A. 3 cm B. 4 cm
C. 5 cm D. 6 cm
二.填空题
1.在Rt△ACB中,∠C=90°,∠A=30°,AB=10,则BC=___5_____.
2.如图所示,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,BE=6 cm,则AC等于 3cm
3.如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM= 5
4.等腰三角形的底角为15°,腰长是2 cm,则腰上的高为_____1cm___.
5.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,如果∠DCB=30°,AB=12,那么BD的长为 3 .
解答题
1.如图,在△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于点D,AB=4,求AD的长.
解:∵∠ACB=90°,∠B=30°,
∴AC=AB=2.
∵∠ACB=90°,
∴∠ACD+∠BCD=90°.
∵CD⊥AB,
∴∠B+∠BCD=90°.
∴∠ACD=∠B=30°.
∴AD=AC=1.
2. 如图,在Rt△ABC中,∠C=90°,∠B=15°,DE垂直平分AB交BC于点E,BE=4,求AC的长.
解:∵DE垂直平分AB,
∴AE=BE=4.
∴∠BAE=∠B=15°.∴∠AEC=∠BAE+∠B=15°+15°=30°.
∵∠C=90°,∴AC=AE=×4=2.
3. 如图,在△ABC中,AB=AC,∠BAC=120°,D为BC的中点,DE⊥AC于点E,AE=8,求CE的长.
解:连接AD.
∵AB=AC,∠BAC=120°,D为BC的中点,
∴AD⊥BC,AD平分∠BAC,∠B=∠C=30°.
∴∠DAC=∠BAC=60°.
∵DE⊥AC于点E,∴∠AED=90°.
∴∠ADE=30°.
在Rt△ADE中,AE=8,∠ADE=30°,
∴AD=2AE=16.
在Rt△ADC中,AD=16,∠C=30°,
∴AC=2AD=32.
∴CE=AC-AE=32-8=24.
4. 如图,四边形ABCD中,AD=4,BC=1,∠A=30°,∠B=90°,∠ADC=120°,求CD的长.
解:延长AD,BC交于点E.
∵∠A=30°,∠B=90°,
∴∠E=60°.
∵∠ADC=120°,
∴∠EDC=60°.
∴△EDC是等边三角形.
设CD=CE=DE=x,∵AD=4,BC=1,
∴2(1+x)=x+4.解得x=2.∴CD=2.
