人教版八年级数学上册14.2乘法公式 随堂练习(含答案)
文档属性
| 名称 | 人教版八年级数学上册14.2乘法公式 随堂练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 206.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-13 15:24:56 | ||
图片预览

文档简介
14.2 乘法公式(随堂练习)-人教版八年级上册
一.选择题
1.如图所示,将四张全等的长方形硬纸片围成一个正方形,根据图形阴影部分面积的关系,可以直观地得到一个关于a、b的恒等式为( )
A.a2﹣b2=(a+b)(a﹣b) B.(a+b)2=a2+2ab+b2
C.(a﹣b)2=(a+b)2﹣4ab D.a2+ab=a(a+b)
2.若x2+2mx+16是完全平方式,则(m﹣1)2+2的值是( )
A.11 B.3 C.11或27 D.3或11
3.对于等式(a+b)2=a2+b2,甲、乙、丙三人有不同看法,则下列说法正确的是( )
甲:无论a和b取何值,等式均不能成立. 乙:只有当a=0时,等式才能成立. 丙:当a=0或b=0时,等式成立.
A.只有甲正确 B.只有乙正确
C.只有丙正确 D.三人说法均不正确
.如图,4张边长分别为a、b的长方形纸片围成一个正方形,从中可以得到的等式是( )
A.(a+b)(a﹣b)=a2﹣b2 B.(a+b)2=a2+2ab+b2
C.(a﹣b)2=a2﹣2ab+b2 D.(a+b)2﹣(a﹣b)2=4ab
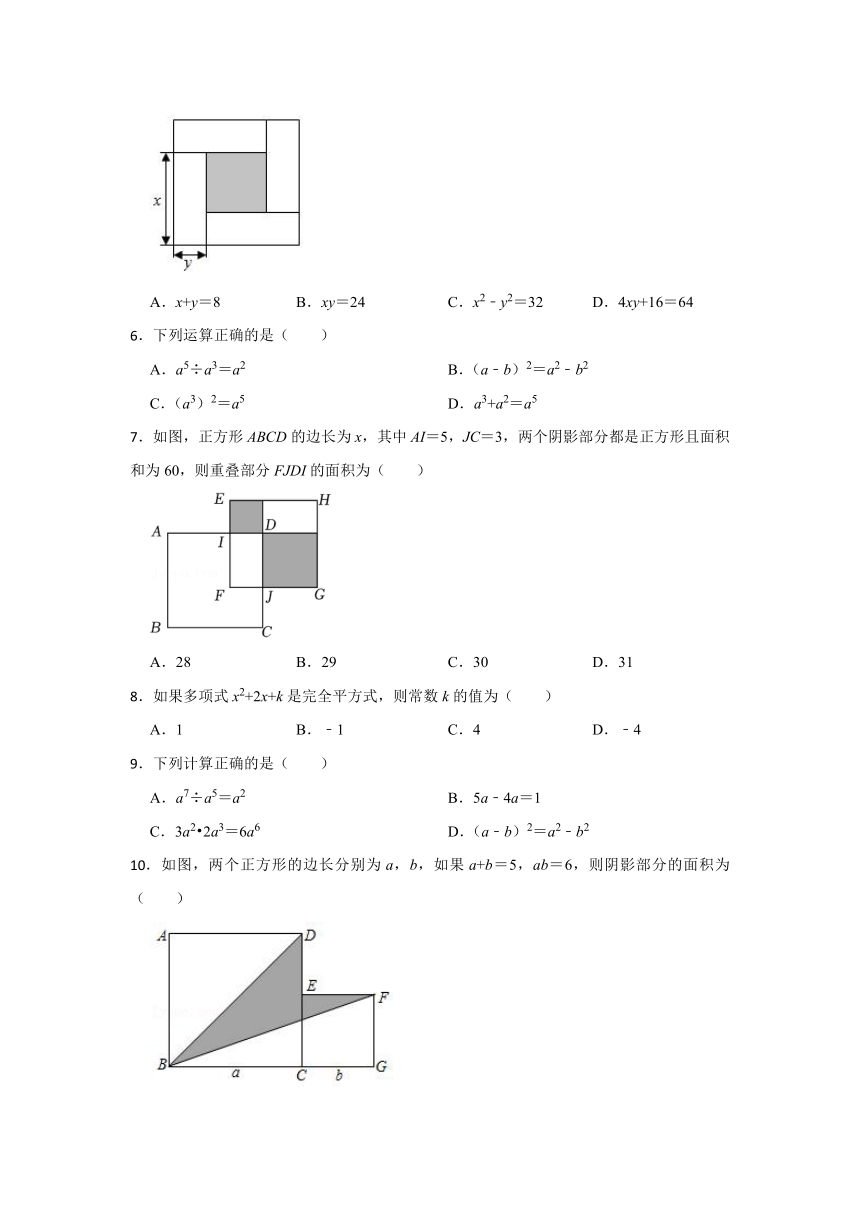
.如图所示的是4个全等的小长方形与1个小正方形密铺而成的正方形图案,已知该图案的面积为64,小正方形的面积为16,若分别为x,y(x>y)表示为小长方形的长和宽,则下列关系式中不正确的是( )
A.x+y=8 B.xy=24 C.x2﹣y2=32 D.4xy+16=64
.下列运算正确的是( )
A.a5÷a3=a2 B.(a﹣b)2=a2﹣b2
C.(a3)2=a5 D.a3+a2=a5
.如图,正方形ABCD的边长为x,其中AI=5,JC=3,两个阴影部分都是正方形且面积和为60,则重叠部分FJDI的面积为( )
A.28 B.29 C.30 D.31
.如果多项式x2+2x+k是完全平方式,则常数k的值为( )
A.1 B.﹣1 C.4 D.﹣4
.下列计算正确的是( )
A.a7÷a5=a2 B.5a﹣4a=1
C.3a2 2a3=6a6 D.(a﹣b)2=a2﹣b2
.如图,两个正方形的边长分别为a,b,如果a+b=5,ab=6,则阴影部分的面积为( )
A.2.5 B.2 C.3.5 D.1
二.填空题
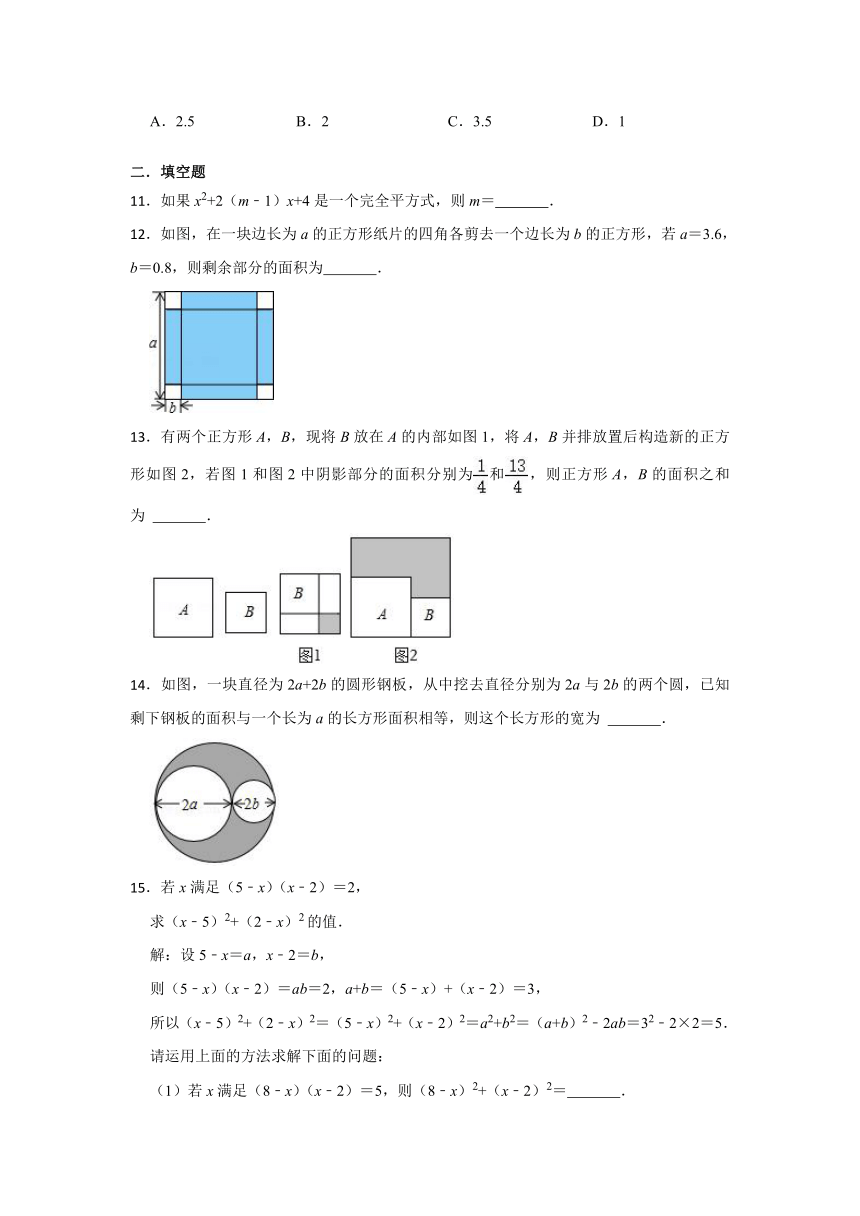
.如果x2+2(m﹣1)x+4是一个完全平方式,则m= .
.如图,在一块边长为a的正方形纸片的四角各剪去一个边长为b的正方形,若a=3.6,b=0.8,则剩余部分的面积为 .
.有两个正方形A,B,现将B放在A的内部如图1,将A,B并排放置后构造新的正方形如图2,若图1和图2中阴影部分的面积分别为和,则正方形A,B的面积之和为 .
.如图,一块直径为2a+2b的圆形钢板,从中挖去直径分别为2a与2b的两个圆,已知剩下钢板的面积与一个长为a的长方形面积相等,则这个长方形的宽为 .
.若x满足(5﹣x)(x﹣2)=2,
求(x﹣5)2+(2﹣x)2的值.
解:设5﹣x=a,x﹣2=b,
则(5﹣x)(x﹣2)=ab=2,a+b=(5﹣x)+(x﹣2)=3,
所以(x﹣5)2+(2﹣x)2=(5﹣x)2+(x﹣2)2=a2+b2=(a+b)2﹣2ab=32﹣2×2=5.
请运用上面的方法求解下面的问题:
(1)若x满足(8﹣x)(x﹣2)=5,则(8﹣x)2+(x﹣2)2= .
(2)已知正方形ABCD的边长为x,E、F分别是AD、DC上的点,且AE=1,CF=3,长方形EMFD的面积是35,则长方形EMFD的周长为 .
三.解答题
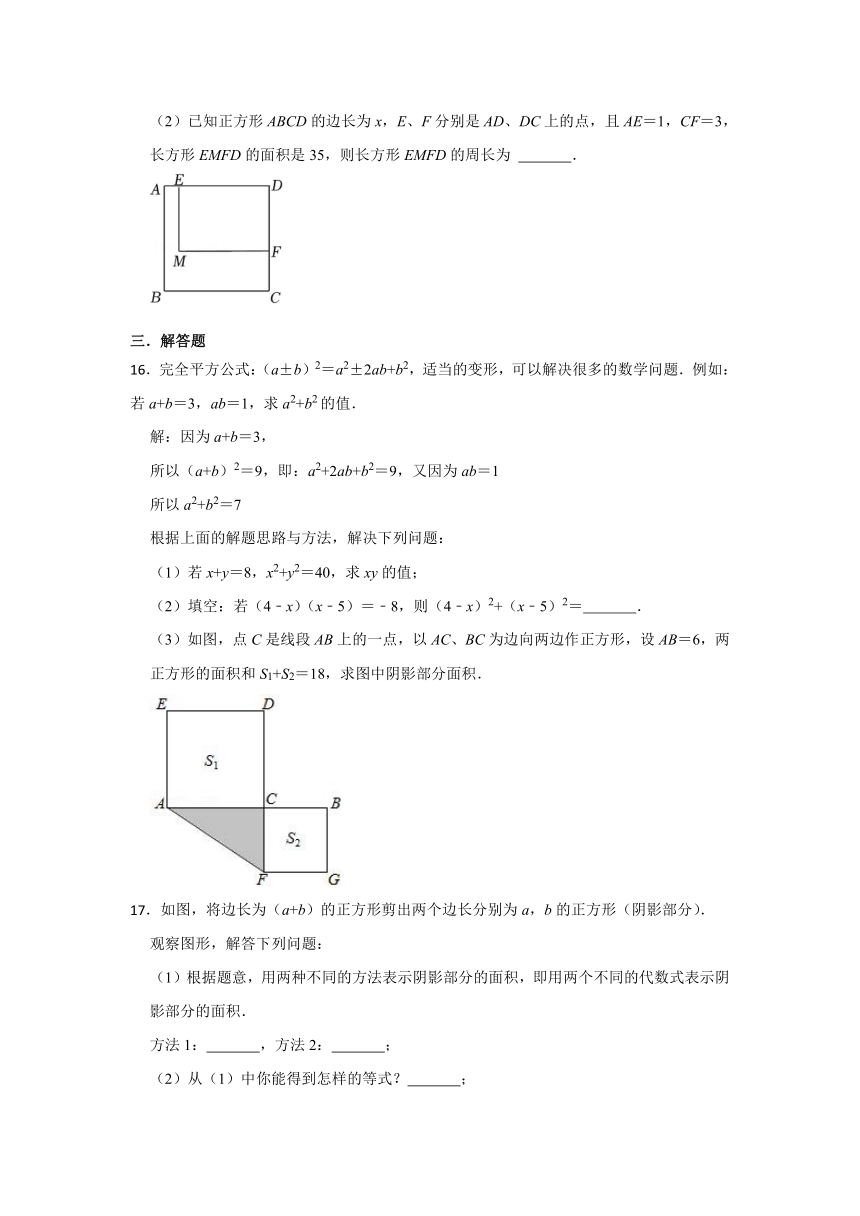
.完全平方公式:(a±b)2=a2±2ab+b2,适当的变形,可以解决很多的数学问题.例如:若a+b=3,ab=1,求a2+b2的值.
解:因为a+b=3,
所以(a+b)2=9,即:a2+2ab+b2=9,又因为ab=1
所以a2+b2=7
根据上面的解题思路与方法,解决下列问题:
(1)若x+y=8,x2+y2=40,求xy的值;
(2)填空:若(4﹣x)(x﹣5)=﹣8,则(4﹣x)2+(x﹣5)2= .
(3)如图,点C是线段AB上的一点,以AC、BC为边向两边作正方形,设AB=6,两正方形的面积和S1+S2=18,求图中阴影部分面积.
.如图,将边长为(a+b)的正方形剪出两个边长分别为a,b的正方形(阴影部分).
观察图形,解答下列问题:
(1)根据题意,用两种不同的方法表示阴影部分的面积,即用两个不同的代数式表示阴影部分的面积.
方法1: ,方法2: ;
(2)从(1)中你能得到怎样的等式? ;
(3)运用你发现的结论,解决下列问题:
①已知x+y=6,xy=2,求x2+y2的值;
②已知(2022﹣x)2+(x﹣2021)2=9,求(2022﹣x)(x﹣2021)的值.
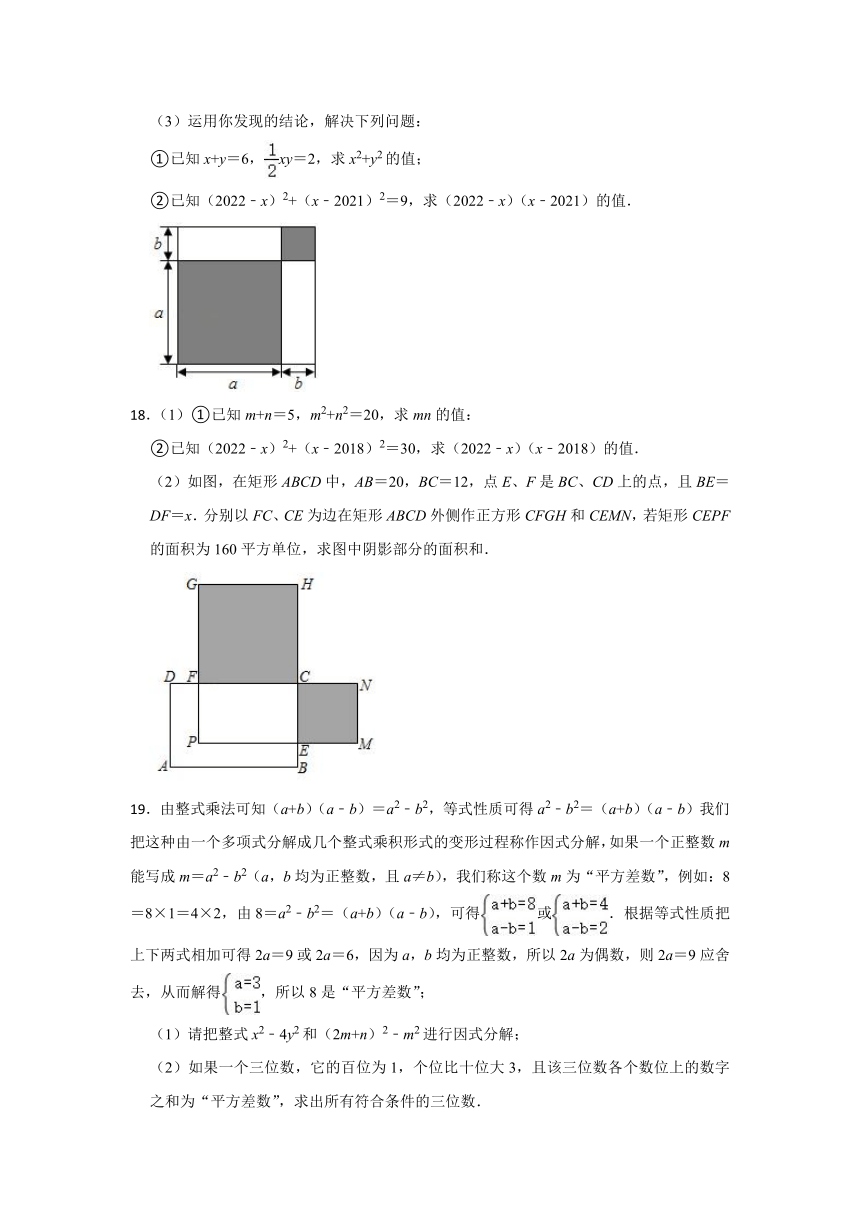
.(1)①已知m+n=5,m2+n2=20,求mn的值:
②已知(2022﹣x)2+(x﹣2018)2=30,求(2022﹣x)(x﹣2018)的值.
(2)如图,在矩形ABCD中,AB=20,BC=12,点E、F是BC、CD上的点,且BE=DF=x.分别以FC、CE为边在矩形ABCD外侧作正方形CFGH和CEMN,若矩形CEPF的面积为160平方单位,求图中阴影部分的面积和.
.由整式乘法可知(a+b)(a﹣b)=a2﹣b2,等式性质可得a2﹣b2=(a+b)(a﹣b)我们把这种由一个多项式分解成几个整式乘积形式的变形过程称作因式分解,如果一个正整数m能写成m=a2﹣b2(a,b均为正整数,且a≠b),我们称这个数m为“平方差数”,例如:8=8×1=4×2,由8=a2﹣b2=(a+b)(a﹣b),可得或.根据等式性质把上下两式相加可得2a=9或2a=6,因为a,b均为正整数,所以2a为偶数,则2a=9应舍去,从而解得,所以8是“平方差数”;
(1)请把整式x2﹣4y2和(2m+n)2﹣m2进行因式分解;
(2)如果一个三位数,它的百位为1,个位比十位大3,且该三位数各个数位上的数字之和为“平方差数”,求出所有符合条件的三位数.
.在学习《整式的乘除》时,对于整式乘法公式的验证,我们经常采用“算两次”的思想.现在有两张大小不一的正方形卡片,边长分别为a、b,小明同学通过用它们进行不同的拼接,验证了两个常见的整式乘法公式,具体拼接方法如下:
(1)若拼接方法如图1所示,阴影部分的面积可以表示为 ,还可以表示为 ,用这两次算面积的结果可以验证哪个等式? .
(2)若拼接方法如图2所示,阴影部分的面积可以表示为 ,还可以表示为 ,用这两次算面积的结果可以验证哪个等式? .
(3)拓展应用:
①若拼接方法如图3所示,且a+b=6,ab=4,则△ABC与△ACD的面积之和为 .
②若拼接方法如图4所示,且a+b=6,a﹣b=4,则△BEF与△ACD的面积之差为 .
参考答案与试题解析
一.选择题
.【解答】解:方法一阴影部分的面积为:(a﹣b)2,
方法二阴影部分的面积为:(a+b)2﹣4ab,
所以根据图形阴影部分面积的关系,可以直观地得到一个关于a、b的恒等式为(a﹣b)2=(a+b)2﹣4ab.
故选:C.
.【解答】解:∵x2+2mx+16是完全平方式.
∴m2=16.
∴m=±4.
当m=4时,(m﹣1)2+2=9+2=11.
当m=﹣4时(m﹣1)2+2=25+2=27.
故答案为:C.
故选:C.
.【解答】解:∵(a+b)2=a2+b2+2ab,
∴当(a+b)2=a2+b2,则a2+2ab+b2=a2+b2.
∴2ab=0.
∴a=0或b=0.
故选:C.
.【解答】解:设大正方形的面积S1,小正方形的面积S2,
大正方形的边长为a+b,则大正方形面积S1=(a+b)2,
小正方形的边长为a﹣b,则小正方形面积S2=(a﹣b)2,
四个长方形的面积为4ab,
∵S1﹣S2=4ab,
∴(a+b)2﹣(a﹣b)2=4ab,
故选:D.
.【解答】解:由题意得:(x+y)2=64且(x﹣y)2=16.(x>y>0).
∴
解得:
∴x+y=8,xy=12,x2﹣y2=32,4xy+16=64.
故选:B.
.【解答】解:a5÷a3=a2,A符合题意;
(a﹣b)2=a2﹣2ab+b2,B不符合题意;
(a3)2=a6,C不符合题意;
a3+a2=a3+a2,D不符合题意;
故选:A.
.【解答】解:设ID=y,DJ=z,
∵两个阴影部分都是正方形,
∴DN=ID=x,DM=DJ=y,
∵四边形ABCD为正方形,
∴AD=CD,
∵AD=AI+ID,CD=CJ+DJ,
∴AI+ID=CJ+DJ,
∵AI=5,CJ=3,
∴5+y=3+z,
∴y=z﹣2,
:∵阴影部分面积和为60,
∴y2+z2=60,
方法1:将y=z﹣2代入y2+z2=60中,得:
(z﹣2)2+z2=60,
解得:z=1+或z=1﹣(舍),
∴y=z﹣2=﹣1,
∴ID=﹣1,DJ=1+,
∴S长方形FJDI=ID DJ=(﹣1)×(1+)=28;
方法2:∵z﹣y=2,
所以(z﹣y)2=4,
∴y2+z2﹣2yz=4,
∴60﹣2yz=4,
yz=28,
∴S长方形FJDI=ID DJ=28.
故选:A.
.【解答】解:∵2x=2×1 x,
∴k=12=1,
故选A.
.【解答】解:∵a7÷a5=a7﹣5=a2,
∴A的计算正确;
∵5a﹣4a=a,
∴B的计算不正确;
∵3a2 2a3=6a5,
∴C选项的计算不正确;
∵(a﹣b)2=a2﹣2ab+b2,
∴D选项的计算不正确,
综上,计算正确的是A,
故选:A.
.【解答】解:S阴影=a2+b2﹣a2﹣b(a+b)=(a2+b2)﹣ab=(a+b)2﹣ab,
把a+b=5,ab=6代入得:
原式=×25﹣×6=3.5.
故选:C.
二.填空题
.【解答】解:∵x2+2(m﹣1)x+4是完全平方式,
∴m﹣1=±2,
m=3或﹣1
故答案为:3或﹣1
.【解答】解:由题意可得:
剩余部分的面积为:a2﹣4b2=(a+2b)(a﹣2b),
将a=3.6,b=0.8代入上式可得:
原式=(3.6+2×0.8)(3.6﹣2×0.8)=10.4.
故答案为:10.4.
.【解答】解:设A的边长为x,B的边长为y,
由甲、乙阴影面积分别是和,可列方程组:
,
将②化简得2xy=③,
由①得x2+y2﹣2xy=,
将③代入可知x2+y2=3.5.
故答案为:3.5.
.【解答】解:设长方形的宽为x,
S阴影=π×(a+b)2﹣π×a2﹣πb2=ax.
∴2πab=ax.
∴x=2πb.
故答案为:2πb.
.【解答】解:(1)设8﹣x=a,x﹣2=b,
则:a+b=6,ab=5.
∴(8﹣x)2+(x﹣2)2=a2+b2=(a+b)2﹣2ab=36﹣10=26.
故答案为:26.
(2)由题意得:DE=x﹣1,DF=x﹣3,
∵长方形EMFD的面积是35.
∴(x﹣1)(x﹣3)=35.
∴设x﹣1=a,x﹣3=b.则:a﹣b=2,ab=35.
∴(a+b)2=(a﹣b)2+4ab=144.
∵a+b>0,
∴a+b=12.
∴四边形EMFD的周长为:2(DE+DF)=2(a+b)=24.
故答案为:24.
三.解答题
.【解答】解:(1)2xy=(x+y)2﹣(x2+y2)=64﹣40=24,
∴xy=12,
(2)由(4﹣x)﹣(5﹣x)=﹣1,
∴[(4﹣x)﹣(5﹣x)]2=(4﹣x)2﹣2(4﹣x)(5﹣x)+(5﹣x)2=(﹣1)2;
又∵(4﹣x)(5﹣x)=8,
∴(4﹣x)2+(5﹣x)2=1+2(4﹣x)(5﹣x)=1+2×8=17;
故答案为:17.
(3)设AC=m,CF=n,
∵AB=6,
∴m+n=6,
又∵S1+S2=18,
∴m2+n2=18,
由完全平方公式可得,(m+n)2=m2+2mn+n2,
∴62=18+2mn,
∴mn=9,
∴S阴影部分=0.5×mn=0.5×9=4.5,
答:阴影部分的面积为4.5.
.【解答】解:(1)方法1,阴影部分的面积等于两个正方形的面积和,即a2+b2,
方法2,从边长为(a+b)的大正方形面积减去两个长为a,宽为b的长方形面积,即(a+b)2﹣2ab,
故答案为:a2+b2,(a+b)2﹣2ab;
(2)∵(1)中的两种方法都表示阴影部分面积,
∴a2+b2=(a+b)2﹣2ab,
故答案为:a2+b2=(a+b)2﹣2ab;
(3)①∵0.5xy=2,
∴xy=4,
又∵x+y=6,
∴x2+y2=(x+y)2﹣2xy
=62﹣2×4
=36﹣8
=28;
②设a=2022﹣x,b=x﹣2021,则a2+b2=9,a+b=1,
∴2(2022﹣x)(x﹣2021)=2ab=(a+b)2﹣(a2+b2)=1﹣9=﹣8,
∴(2022﹣x)(x﹣2021)=﹣4,
答:(2022﹣x)(x﹣2021)的值为﹣4.
.【解答】解:(1)①∵m+n=5,m2+n2=20,(m+n)2=m2+n2+2mn,
∴25=20+2mn,
∴mn=;
②设a=2022﹣x,b=x﹣2018,则a+b=4,a2+b2=(2022﹣x)2+(x﹣2018)2=30,
由(a+b)2=a2+b2+2ab得,
16=30+2ab,
即ab=﹣7
∴(2022﹣x)(x﹣2018)=﹣7;
(2)∵AB=20,BC=12,BE=DF=x,
∴FC=AB﹣DF=20﹣x,CE=BC﹣BE=12﹣x,
设p=20﹣x,q=12﹣x,则p﹣q=8,
由于矩形CEPF的面积为160平方单位,即pq=160,
∴p2+q2=(p﹣q)2+2pq=64+320=384(平方单位),
即阴影部分的面积和为384平方单位.
.【解答】解:(1)x2﹣4y2=x2﹣(2y)2=(x+2y)(x﹣2y),
(2m+n)2﹣m2=(2m+n+m)(2m+n﹣m)=(3m+n)(m+n);
(2)设该三位数十位上的数字为x,则其各个数位上的数字之和为1+x+(x+3)=2x+4=2(x+2),
由2(x+2)=a2﹣b2=(a+b)(a﹣b),可得或,
可得2a=x+4,
∴x是偶数,
当x=0时,x+3=3,
∴该三位数是103;
当x=2,x+3=5,
∴该三位数是125,
x=4,x+3=7,
∴该三位数是147;
当x=6时,x+3=9,
∴该三位数是169,
∴所有符合条件的三位数为103,125,147或169.
.【解答】解:(1)阴影部分面积为:a2﹣b2,
还可以表示为:a(a﹣b)+b(a﹣b)=(a﹣b)(a+b),
则有:a2﹣b2=(a﹣b)(a+b);
故答案为:a2﹣b2;(a﹣b)(a+b);a2﹣b2=(a﹣b)(a+b);
(2)阴影部分面积为:(a+b)2﹣2ab,
还可以表示为:a2+b2,
则有:(a+b)2﹣2ab=a2+b2;
故答案为:(a+b)2﹣2ab;a2+b2;(a+b)2﹣2ab=a2+b2;
(3)①阴影部分面积为:
a2+b2﹣[a(a+b)+b2]
=a2+b2﹣ab
=(a2+b2)﹣ab
=(a+b)2﹣ab﹣ab
=(a+b)2﹣ab,
∵a+b=6,ab=4,
∴原式=
=18﹣6
=12;
即△ABC与△ACD的面积之和为12.
故答案为:12;
②S△BEF=a2+b2﹣a2﹣b(a+b)+b(a﹣b)=,
S△ACD=a2+b2﹣a(a﹣b)﹣a(a+b)﹣b2=b2,
∴△BEF与△ACD的面积之差为:﹣=(a2﹣b2)=(a﹣b)(a+b),
∵a+b=6,a﹣b=4,
∴原式=×6×4
=12.
故答案为:12.
一.选择题
1.如图所示,将四张全等的长方形硬纸片围成一个正方形,根据图形阴影部分面积的关系,可以直观地得到一个关于a、b的恒等式为( )
A.a2﹣b2=(a+b)(a﹣b) B.(a+b)2=a2+2ab+b2
C.(a﹣b)2=(a+b)2﹣4ab D.a2+ab=a(a+b)
2.若x2+2mx+16是完全平方式,则(m﹣1)2+2的值是( )
A.11 B.3 C.11或27 D.3或11
3.对于等式(a+b)2=a2+b2,甲、乙、丙三人有不同看法,则下列说法正确的是( )
甲:无论a和b取何值,等式均不能成立. 乙:只有当a=0时,等式才能成立. 丙:当a=0或b=0时,等式成立.
A.只有甲正确 B.只有乙正确
C.只有丙正确 D.三人说法均不正确
.如图,4张边长分别为a、b的长方形纸片围成一个正方形,从中可以得到的等式是( )
A.(a+b)(a﹣b)=a2﹣b2 B.(a+b)2=a2+2ab+b2
C.(a﹣b)2=a2﹣2ab+b2 D.(a+b)2﹣(a﹣b)2=4ab
.如图所示的是4个全等的小长方形与1个小正方形密铺而成的正方形图案,已知该图案的面积为64,小正方形的面积为16,若分别为x,y(x>y)表示为小长方形的长和宽,则下列关系式中不正确的是( )
A.x+y=8 B.xy=24 C.x2﹣y2=32 D.4xy+16=64
.下列运算正确的是( )
A.a5÷a3=a2 B.(a﹣b)2=a2﹣b2
C.(a3)2=a5 D.a3+a2=a5
.如图,正方形ABCD的边长为x,其中AI=5,JC=3,两个阴影部分都是正方形且面积和为60,则重叠部分FJDI的面积为( )
A.28 B.29 C.30 D.31
.如果多项式x2+2x+k是完全平方式,则常数k的值为( )
A.1 B.﹣1 C.4 D.﹣4
.下列计算正确的是( )
A.a7÷a5=a2 B.5a﹣4a=1
C.3a2 2a3=6a6 D.(a﹣b)2=a2﹣b2
.如图,两个正方形的边长分别为a,b,如果a+b=5,ab=6,则阴影部分的面积为( )
A.2.5 B.2 C.3.5 D.1
二.填空题
.如果x2+2(m﹣1)x+4是一个完全平方式,则m= .
.如图,在一块边长为a的正方形纸片的四角各剪去一个边长为b的正方形,若a=3.6,b=0.8,则剩余部分的面积为 .
.有两个正方形A,B,现将B放在A的内部如图1,将A,B并排放置后构造新的正方形如图2,若图1和图2中阴影部分的面积分别为和,则正方形A,B的面积之和为 .
.如图,一块直径为2a+2b的圆形钢板,从中挖去直径分别为2a与2b的两个圆,已知剩下钢板的面积与一个长为a的长方形面积相等,则这个长方形的宽为 .
.若x满足(5﹣x)(x﹣2)=2,
求(x﹣5)2+(2﹣x)2的值.
解:设5﹣x=a,x﹣2=b,
则(5﹣x)(x﹣2)=ab=2,a+b=(5﹣x)+(x﹣2)=3,
所以(x﹣5)2+(2﹣x)2=(5﹣x)2+(x﹣2)2=a2+b2=(a+b)2﹣2ab=32﹣2×2=5.
请运用上面的方法求解下面的问题:
(1)若x满足(8﹣x)(x﹣2)=5,则(8﹣x)2+(x﹣2)2= .
(2)已知正方形ABCD的边长为x,E、F分别是AD、DC上的点,且AE=1,CF=3,长方形EMFD的面积是35,则长方形EMFD的周长为 .
三.解答题
.完全平方公式:(a±b)2=a2±2ab+b2,适当的变形,可以解决很多的数学问题.例如:若a+b=3,ab=1,求a2+b2的值.
解:因为a+b=3,
所以(a+b)2=9,即:a2+2ab+b2=9,又因为ab=1
所以a2+b2=7
根据上面的解题思路与方法,解决下列问题:
(1)若x+y=8,x2+y2=40,求xy的值;
(2)填空:若(4﹣x)(x﹣5)=﹣8,则(4﹣x)2+(x﹣5)2= .
(3)如图,点C是线段AB上的一点,以AC、BC为边向两边作正方形,设AB=6,两正方形的面积和S1+S2=18,求图中阴影部分面积.
.如图,将边长为(a+b)的正方形剪出两个边长分别为a,b的正方形(阴影部分).
观察图形,解答下列问题:
(1)根据题意,用两种不同的方法表示阴影部分的面积,即用两个不同的代数式表示阴影部分的面积.
方法1: ,方法2: ;
(2)从(1)中你能得到怎样的等式? ;
(3)运用你发现的结论,解决下列问题:
①已知x+y=6,xy=2,求x2+y2的值;
②已知(2022﹣x)2+(x﹣2021)2=9,求(2022﹣x)(x﹣2021)的值.
.(1)①已知m+n=5,m2+n2=20,求mn的值:
②已知(2022﹣x)2+(x﹣2018)2=30,求(2022﹣x)(x﹣2018)的值.
(2)如图,在矩形ABCD中,AB=20,BC=12,点E、F是BC、CD上的点,且BE=DF=x.分别以FC、CE为边在矩形ABCD外侧作正方形CFGH和CEMN,若矩形CEPF的面积为160平方单位,求图中阴影部分的面积和.
.由整式乘法可知(a+b)(a﹣b)=a2﹣b2,等式性质可得a2﹣b2=(a+b)(a﹣b)我们把这种由一个多项式分解成几个整式乘积形式的变形过程称作因式分解,如果一个正整数m能写成m=a2﹣b2(a,b均为正整数,且a≠b),我们称这个数m为“平方差数”,例如:8=8×1=4×2,由8=a2﹣b2=(a+b)(a﹣b),可得或.根据等式性质把上下两式相加可得2a=9或2a=6,因为a,b均为正整数,所以2a为偶数,则2a=9应舍去,从而解得,所以8是“平方差数”;
(1)请把整式x2﹣4y2和(2m+n)2﹣m2进行因式分解;
(2)如果一个三位数,它的百位为1,个位比十位大3,且该三位数各个数位上的数字之和为“平方差数”,求出所有符合条件的三位数.
.在学习《整式的乘除》时,对于整式乘法公式的验证,我们经常采用“算两次”的思想.现在有两张大小不一的正方形卡片,边长分别为a、b,小明同学通过用它们进行不同的拼接,验证了两个常见的整式乘法公式,具体拼接方法如下:
(1)若拼接方法如图1所示,阴影部分的面积可以表示为 ,还可以表示为 ,用这两次算面积的结果可以验证哪个等式? .
(2)若拼接方法如图2所示,阴影部分的面积可以表示为 ,还可以表示为 ,用这两次算面积的结果可以验证哪个等式? .
(3)拓展应用:
①若拼接方法如图3所示,且a+b=6,ab=4,则△ABC与△ACD的面积之和为 .
②若拼接方法如图4所示,且a+b=6,a﹣b=4,则△BEF与△ACD的面积之差为 .
参考答案与试题解析
一.选择题
.【解答】解:方法一阴影部分的面积为:(a﹣b)2,
方法二阴影部分的面积为:(a+b)2﹣4ab,
所以根据图形阴影部分面积的关系,可以直观地得到一个关于a、b的恒等式为(a﹣b)2=(a+b)2﹣4ab.
故选:C.
.【解答】解:∵x2+2mx+16是完全平方式.
∴m2=16.
∴m=±4.
当m=4时,(m﹣1)2+2=9+2=11.
当m=﹣4时(m﹣1)2+2=25+2=27.
故答案为:C.
故选:C.
.【解答】解:∵(a+b)2=a2+b2+2ab,
∴当(a+b)2=a2+b2,则a2+2ab+b2=a2+b2.
∴2ab=0.
∴a=0或b=0.
故选:C.
.【解答】解:设大正方形的面积S1,小正方形的面积S2,
大正方形的边长为a+b,则大正方形面积S1=(a+b)2,
小正方形的边长为a﹣b,则小正方形面积S2=(a﹣b)2,
四个长方形的面积为4ab,
∵S1﹣S2=4ab,
∴(a+b)2﹣(a﹣b)2=4ab,
故选:D.
.【解答】解:由题意得:(x+y)2=64且(x﹣y)2=16.(x>y>0).
∴
解得:
∴x+y=8,xy=12,x2﹣y2=32,4xy+16=64.
故选:B.
.【解答】解:a5÷a3=a2,A符合题意;
(a﹣b)2=a2﹣2ab+b2,B不符合题意;
(a3)2=a6,C不符合题意;
a3+a2=a3+a2,D不符合题意;
故选:A.
.【解答】解:设ID=y,DJ=z,
∵两个阴影部分都是正方形,
∴DN=ID=x,DM=DJ=y,
∵四边形ABCD为正方形,
∴AD=CD,
∵AD=AI+ID,CD=CJ+DJ,
∴AI+ID=CJ+DJ,
∵AI=5,CJ=3,
∴5+y=3+z,
∴y=z﹣2,
:∵阴影部分面积和为60,
∴y2+z2=60,
方法1:将y=z﹣2代入y2+z2=60中,得:
(z﹣2)2+z2=60,
解得:z=1+或z=1﹣(舍),
∴y=z﹣2=﹣1,
∴ID=﹣1,DJ=1+,
∴S长方形FJDI=ID DJ=(﹣1)×(1+)=28;
方法2:∵z﹣y=2,
所以(z﹣y)2=4,
∴y2+z2﹣2yz=4,
∴60﹣2yz=4,
yz=28,
∴S长方形FJDI=ID DJ=28.
故选:A.
.【解答】解:∵2x=2×1 x,
∴k=12=1,
故选A.
.【解答】解:∵a7÷a5=a7﹣5=a2,
∴A的计算正确;
∵5a﹣4a=a,
∴B的计算不正确;
∵3a2 2a3=6a5,
∴C选项的计算不正确;
∵(a﹣b)2=a2﹣2ab+b2,
∴D选项的计算不正确,
综上,计算正确的是A,
故选:A.
.【解答】解:S阴影=a2+b2﹣a2﹣b(a+b)=(a2+b2)﹣ab=(a+b)2﹣ab,
把a+b=5,ab=6代入得:
原式=×25﹣×6=3.5.
故选:C.
二.填空题
.【解答】解:∵x2+2(m﹣1)x+4是完全平方式,
∴m﹣1=±2,
m=3或﹣1
故答案为:3或﹣1
.【解答】解:由题意可得:
剩余部分的面积为:a2﹣4b2=(a+2b)(a﹣2b),
将a=3.6,b=0.8代入上式可得:
原式=(3.6+2×0.8)(3.6﹣2×0.8)=10.4.
故答案为:10.4.
.【解答】解:设A的边长为x,B的边长为y,
由甲、乙阴影面积分别是和,可列方程组:
,
将②化简得2xy=③,
由①得x2+y2﹣2xy=,
将③代入可知x2+y2=3.5.
故答案为:3.5.
.【解答】解:设长方形的宽为x,
S阴影=π×(a+b)2﹣π×a2﹣πb2=ax.
∴2πab=ax.
∴x=2πb.
故答案为:2πb.
.【解答】解:(1)设8﹣x=a,x﹣2=b,
则:a+b=6,ab=5.
∴(8﹣x)2+(x﹣2)2=a2+b2=(a+b)2﹣2ab=36﹣10=26.
故答案为:26.
(2)由题意得:DE=x﹣1,DF=x﹣3,
∵长方形EMFD的面积是35.
∴(x﹣1)(x﹣3)=35.
∴设x﹣1=a,x﹣3=b.则:a﹣b=2,ab=35.
∴(a+b)2=(a﹣b)2+4ab=144.
∵a+b>0,
∴a+b=12.
∴四边形EMFD的周长为:2(DE+DF)=2(a+b)=24.
故答案为:24.
三.解答题
.【解答】解:(1)2xy=(x+y)2﹣(x2+y2)=64﹣40=24,
∴xy=12,
(2)由(4﹣x)﹣(5﹣x)=﹣1,
∴[(4﹣x)﹣(5﹣x)]2=(4﹣x)2﹣2(4﹣x)(5﹣x)+(5﹣x)2=(﹣1)2;
又∵(4﹣x)(5﹣x)=8,
∴(4﹣x)2+(5﹣x)2=1+2(4﹣x)(5﹣x)=1+2×8=17;
故答案为:17.
(3)设AC=m,CF=n,
∵AB=6,
∴m+n=6,
又∵S1+S2=18,
∴m2+n2=18,
由完全平方公式可得,(m+n)2=m2+2mn+n2,
∴62=18+2mn,
∴mn=9,
∴S阴影部分=0.5×mn=0.5×9=4.5,
答:阴影部分的面积为4.5.
.【解答】解:(1)方法1,阴影部分的面积等于两个正方形的面积和,即a2+b2,
方法2,从边长为(a+b)的大正方形面积减去两个长为a,宽为b的长方形面积,即(a+b)2﹣2ab,
故答案为:a2+b2,(a+b)2﹣2ab;
(2)∵(1)中的两种方法都表示阴影部分面积,
∴a2+b2=(a+b)2﹣2ab,
故答案为:a2+b2=(a+b)2﹣2ab;
(3)①∵0.5xy=2,
∴xy=4,
又∵x+y=6,
∴x2+y2=(x+y)2﹣2xy
=62﹣2×4
=36﹣8
=28;
②设a=2022﹣x,b=x﹣2021,则a2+b2=9,a+b=1,
∴2(2022﹣x)(x﹣2021)=2ab=(a+b)2﹣(a2+b2)=1﹣9=﹣8,
∴(2022﹣x)(x﹣2021)=﹣4,
答:(2022﹣x)(x﹣2021)的值为﹣4.
.【解答】解:(1)①∵m+n=5,m2+n2=20,(m+n)2=m2+n2+2mn,
∴25=20+2mn,
∴mn=;
②设a=2022﹣x,b=x﹣2018,则a+b=4,a2+b2=(2022﹣x)2+(x﹣2018)2=30,
由(a+b)2=a2+b2+2ab得,
16=30+2ab,
即ab=﹣7
∴(2022﹣x)(x﹣2018)=﹣7;
(2)∵AB=20,BC=12,BE=DF=x,
∴FC=AB﹣DF=20﹣x,CE=BC﹣BE=12﹣x,
设p=20﹣x,q=12﹣x,则p﹣q=8,
由于矩形CEPF的面积为160平方单位,即pq=160,
∴p2+q2=(p﹣q)2+2pq=64+320=384(平方单位),
即阴影部分的面积和为384平方单位.
.【解答】解:(1)x2﹣4y2=x2﹣(2y)2=(x+2y)(x﹣2y),
(2m+n)2﹣m2=(2m+n+m)(2m+n﹣m)=(3m+n)(m+n);
(2)设该三位数十位上的数字为x,则其各个数位上的数字之和为1+x+(x+3)=2x+4=2(x+2),
由2(x+2)=a2﹣b2=(a+b)(a﹣b),可得或,
可得2a=x+4,
∴x是偶数,
当x=0时,x+3=3,
∴该三位数是103;
当x=2,x+3=5,
∴该三位数是125,
x=4,x+3=7,
∴该三位数是147;
当x=6时,x+3=9,
∴该三位数是169,
∴所有符合条件的三位数为103,125,147或169.
.【解答】解:(1)阴影部分面积为:a2﹣b2,
还可以表示为:a(a﹣b)+b(a﹣b)=(a﹣b)(a+b),
则有:a2﹣b2=(a﹣b)(a+b);
故答案为:a2﹣b2;(a﹣b)(a+b);a2﹣b2=(a﹣b)(a+b);
(2)阴影部分面积为:(a+b)2﹣2ab,
还可以表示为:a2+b2,
则有:(a+b)2﹣2ab=a2+b2;
故答案为:(a+b)2﹣2ab;a2+b2;(a+b)2﹣2ab=a2+b2;
(3)①阴影部分面积为:
a2+b2﹣[a(a+b)+b2]
=a2+b2﹣ab
=(a2+b2)﹣ab
=(a+b)2﹣ab﹣ab
=(a+b)2﹣ab,
∵a+b=6,ab=4,
∴原式=
=18﹣6
=12;
即△ABC与△ACD的面积之和为12.
故答案为:12;
②S△BEF=a2+b2﹣a2﹣b(a+b)+b(a﹣b)=,
S△ACD=a2+b2﹣a(a﹣b)﹣a(a+b)﹣b2=b2,
∴△BEF与△ACD的面积之差为:﹣=(a2﹣b2)=(a﹣b)(a+b),
∵a+b=6,a﹣b=4,
∴原式=×6×4
=12.
故答案为:12.
