人教版八年级数学上册13.3等腰三角形 提升题(word,无答案)
文档属性
| 名称 | 人教版八年级数学上册13.3等腰三角形 提升题(word,无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 264.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-13 15:26:30 | ||
图片预览

文档简介
13.3 等腰三角形(提升题)-2022年人教版数学八年级上册
一.选择题
51.如图,∠C=∠B,AF⊥BC,垂足为F,点E在BC上,且CD=CE,∠A=34°,则∠D的度数为( )
A.34° B.52° C.56° D.62°
52.下列说法正确的是( )
A.直线外一点与直线上各点连接的线段中,垂线段最短
B.三角形的三条高线交于一点
C.过一点有且只有一条直线与已知直线垂直
D.等腰三角形的高线、中线、角平分线三线重合,也称“三线合一”
53.若等腰三角形的两边长为4和8,则该等腰三角形的第三边为( )
A.4 B.6 C.8 D.4或8
54.如图,在△ABC中,AB=AC=BC,高AD=h,则AB的长为( )
A. B. C.h D.2h
55.若x、y为等腰三角形的两边,且满足|x﹣4|+(x﹣y+2)2=0,则这个等腰三角形的周长为( )
A.16 B.14 C.10 D.16或14
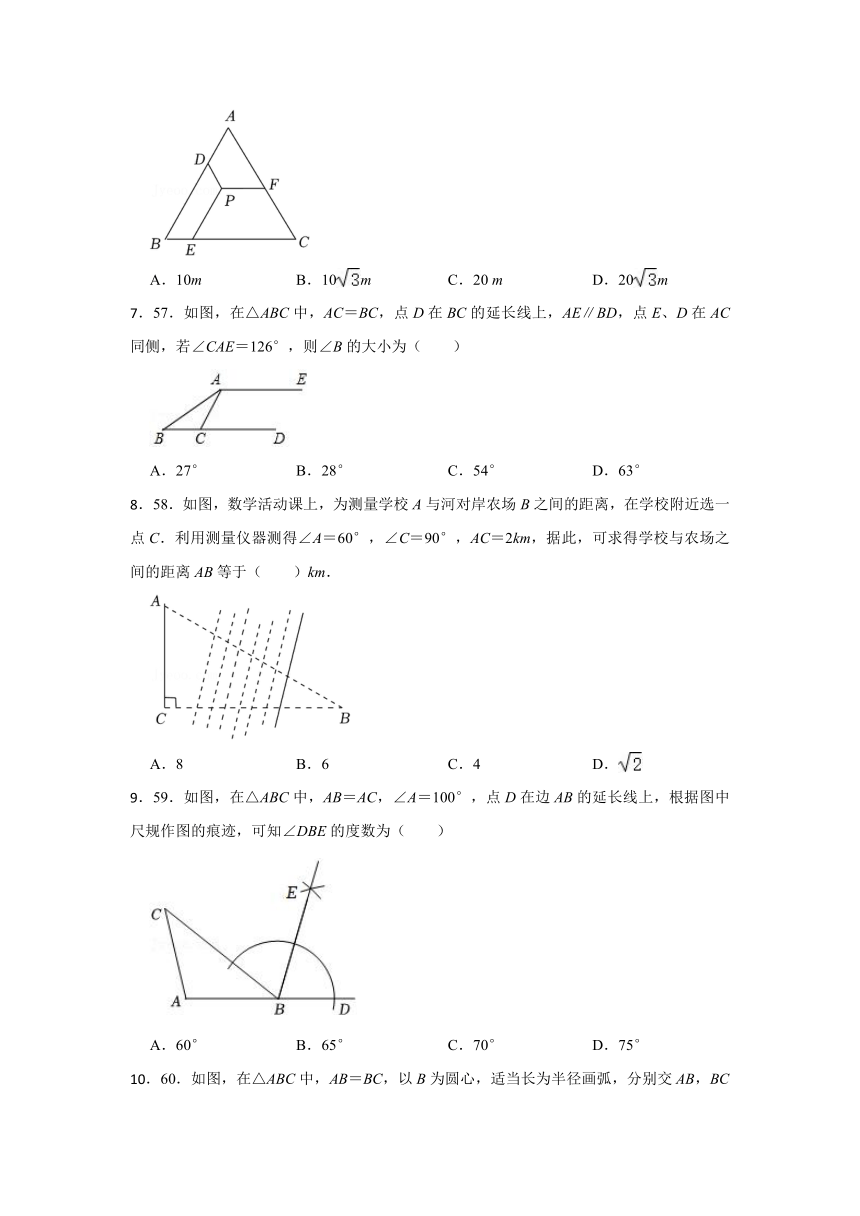
56.如图,等边三角形ABC是一块边长为20m的草坪,点P是草坪内的任意一点,过点P有三条小路PD,PE,PF,且满足PE∥AB,PF∥BC,PD∥AC,则三条小路的总长度为( )
A.10m B.10m C.20 m D.20m
57.如图,在△ABC中,AC=BC,点D在BC的延长线上,AE∥BD,点E、D在AC同侧,若∠CAE=126°,则∠B的大小为( )
A.27° B.28° C.54° D.63°
58.如图,数学活动课上,为测量学校A与河对岸农场B之间的距离,在学校附近选一点C.利用测量仪器测得∠A=60°,∠C=90°,AC=2km,据此,可求得学校与农场之间的距离AB等于( )km.
A.8 B.6 C.4 D.
59.如图,在△ABC中,AB=AC,∠A=100°,点D在边AB的延长线上,根据图中尺规作图的痕迹,可知∠DBE的度数为( )
A.60° B.65° C.70° D.75°
60.如图,在△ABC中,AB=BC,以B为圆心,适当长为半径画弧,分别交AB,BC于点M,N,分别以M,N为圆心,大于MN的长为半径画弧,两弧在∠ABC内部交于点D,作射线BD交AC于点E,点F为BC的中点,连接EF.若BE=AC=2,则△CEF的周长为( )
A.2+1 B.+1 C.+2 D.4
二.填空题
26.如图,在△ABC中,AB=AC,∠C=30°,点D在BC上,AB⊥AD,AD=3cm,则BC的长为 cm.
27.腰长为2a,底角为15°的等腰三角形的面积为 .
28.如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,若△ABC的面积为10,则图中阴影部分的面积为 .
29.已知|x﹣4|+(y﹣2)2=0,则以x,y的值为两边长的等腰三角形的周长为 .
30.如图,在△ABC中,∠A=70°,∠C=30°,点D为AC边上一点,过点D作DE∥AB,交BC于点E,且DE=BE,连接BD,则∠BDC的度数是 .
三.解答题
26.如图,在△ABC中,∠B=30°,∠C=45°,EP是AB边的垂直平分线,FQ是AC边的垂直平分线,连接AE,AF,若AB=12,求EF的长.
27.如图,△ABC是边长为10cm的等边三角形,动点P从点B出发以3cm/s速度沿着B→A→C→B向终点B运动,同时动点Q从点C出发以2cm/s速度沿着C→B→A→C向终点C运动,运动时间为t秒.
(1)当P在AB边上运动时,BP= ,BQ= .
(2)当PQ∥AC时,求t的值.
28.如图,AE平分∠BAC,AC=CE.
(1)求证:AB∥CD.
(2)若∠C=50°,求∠AED的度数.
29.如图,在△ABC中,点O是边AC上一个动点,过点O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长.
30.已知:在△ABC中,AB=AC,∠A=36°,CD是△ABC的角平分线.
(1)如图1,求证:AD=BC;
(2)如图2,过点D作DE∥BC交AC于点E,在不添加任何辅助线的情况下,请直接写出图2中的四个等腰三角形(△ABC除外).
一.选择题
51.如图,∠C=∠B,AF⊥BC,垂足为F,点E在BC上,且CD=CE,∠A=34°,则∠D的度数为( )
A.34° B.52° C.56° D.62°
52.下列说法正确的是( )
A.直线外一点与直线上各点连接的线段中,垂线段最短
B.三角形的三条高线交于一点
C.过一点有且只有一条直线与已知直线垂直
D.等腰三角形的高线、中线、角平分线三线重合,也称“三线合一”
53.若等腰三角形的两边长为4和8,则该等腰三角形的第三边为( )
A.4 B.6 C.8 D.4或8
54.如图,在△ABC中,AB=AC=BC,高AD=h,则AB的长为( )
A. B. C.h D.2h
55.若x、y为等腰三角形的两边,且满足|x﹣4|+(x﹣y+2)2=0,则这个等腰三角形的周长为( )
A.16 B.14 C.10 D.16或14
56.如图,等边三角形ABC是一块边长为20m的草坪,点P是草坪内的任意一点,过点P有三条小路PD,PE,PF,且满足PE∥AB,PF∥BC,PD∥AC,则三条小路的总长度为( )
A.10m B.10m C.20 m D.20m
57.如图,在△ABC中,AC=BC,点D在BC的延长线上,AE∥BD,点E、D在AC同侧,若∠CAE=126°,则∠B的大小为( )
A.27° B.28° C.54° D.63°
58.如图,数学活动课上,为测量学校A与河对岸农场B之间的距离,在学校附近选一点C.利用测量仪器测得∠A=60°,∠C=90°,AC=2km,据此,可求得学校与农场之间的距离AB等于( )km.
A.8 B.6 C.4 D.
59.如图,在△ABC中,AB=AC,∠A=100°,点D在边AB的延长线上,根据图中尺规作图的痕迹,可知∠DBE的度数为( )
A.60° B.65° C.70° D.75°
60.如图,在△ABC中,AB=BC,以B为圆心,适当长为半径画弧,分别交AB,BC于点M,N,分别以M,N为圆心,大于MN的长为半径画弧,两弧在∠ABC内部交于点D,作射线BD交AC于点E,点F为BC的中点,连接EF.若BE=AC=2,则△CEF的周长为( )
A.2+1 B.+1 C.+2 D.4
二.填空题
26.如图,在△ABC中,AB=AC,∠C=30°,点D在BC上,AB⊥AD,AD=3cm,则BC的长为 cm.
27.腰长为2a,底角为15°的等腰三角形的面积为 .
28.如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,若△ABC的面积为10,则图中阴影部分的面积为 .
29.已知|x﹣4|+(y﹣2)2=0,则以x,y的值为两边长的等腰三角形的周长为 .
30.如图,在△ABC中,∠A=70°,∠C=30°,点D为AC边上一点,过点D作DE∥AB,交BC于点E,且DE=BE,连接BD,则∠BDC的度数是 .
三.解答题
26.如图,在△ABC中,∠B=30°,∠C=45°,EP是AB边的垂直平分线,FQ是AC边的垂直平分线,连接AE,AF,若AB=12,求EF的长.
27.如图,△ABC是边长为10cm的等边三角形,动点P从点B出发以3cm/s速度沿着B→A→C→B向终点B运动,同时动点Q从点C出发以2cm/s速度沿着C→B→A→C向终点C运动,运动时间为t秒.
(1)当P在AB边上运动时,BP= ,BQ= .
(2)当PQ∥AC时,求t的值.
28.如图,AE平分∠BAC,AC=CE.
(1)求证:AB∥CD.
(2)若∠C=50°,求∠AED的度数.
29.如图,在△ABC中,点O是边AC上一个动点,过点O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长.
30.已知:在△ABC中,AB=AC,∠A=36°,CD是△ABC的角平分线.
(1)如图1,求证:AD=BC;
(2)如图2,过点D作DE∥BC交AC于点E,在不添加任何辅助线的情况下,请直接写出图2中的四个等腰三角形(△ABC除外).
