2013-2014学年冀教版九年级数学下学期期中检测题及答案解析
文档属性
| 名称 | 2013-2014学年冀教版九年级数学下学期期中检测题及答案解析 |
|
|
| 格式 | zip | ||
| 文件大小 | 311.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-11-07 00:00:00 | ||
图片预览




文档简介
期中检测题
(本检测题满分:120分,时间:120分钟)
一、选择题(每小题3分,共36分)
1.下列说法正确的是( )
A.过一点的圆的圆心可以是平面上任意点
B.过两点的圆的圆心在一条直线上
C.过三点的圆的圆心有且只有一点
D.过四点的圆不存在
2.(2013 江西中考)若二次函数的图像与轴有两个交点,坐标分别为且图像上有一点在轴下方,则下列判断正确的 是( )
A. B.
C. D.
3.已知两圆的半径分别为,且这两圆有公共点,则这两圆的圆心距为( )
A.4 B.10 C.4或10 D.
4.在△中,∠°,,以为圆心作和相切,则的半径长为( )
A.8 B.4 C.9.6 D.4.8
5.(2013 南京中考)如图,⊙、⊙的圆心、在直线l上,⊙的半径为2 cm,⊙的半径为3 cm,=8 cm.⊙以1 cm/s的速度沿直线l向右运动,7 s后停止运动.在此过程中,⊙与⊙没有出现的位置关系是( )
A.外切 B.相交 C.内切 D.内含
第5题图
6.一次函数与二次函数在同一坐标系中的图像可能是( )
7.已知抛物线的顶点坐标是,则和的值分别是( )
A.2,4 B. C.2, D.,0
8.对于函数,使得随的增大而增大的的取值范围是( )
A. B. C. D.
9.对于任意实数,抛物线 总经过一个固定的点,这个点是( )
A. (1, 0) B.(, 0) C.(, 3) D. (1, 3)
10.已知抛物线经过原点和第一、二、三象限,那么( )
A. B.
C. D.
11.若(2, 5)、(4, 5)是抛物线上的两点,则它的对称轴是( )
A. B. C. D.
12.小敏在今年的校运动会跳远比赛中跳出了满意一跳,函数(的单位:s,的单位:m)可以描述他跳跃时重心高度的变化.则他起跳后到重心最高时所用的时间
是( )
A.0.71 s B.0.70 s C.0.63 s D.0.36 s
二、填空题(每小题3分,共24分)
13.锐角三角形的外心在__________;直角三角形的外心在__________;钝角三角形的外心
在___________.
14.如图,已知为的直径,是的切线,为切点,
,则的度数为______.
15.已知和的半径分别是一元二次方程的两根,
且则和的位置关系是_______.
16.对于二次函数,已知当由1增加到2时,函数值减少3,则常
数的值是 .
17.将抛物线向右平移2个单位后,再向下平移5个单位,所得抛物线的顶点坐标为_______.
18.设三点依次分别是抛物线与轴的交点以及与轴的两个交点,则△的面积是 .
19.函数写成的形式是________,其图像的顶点坐标是
_______,对称轴是__________.
20.有一个二次函数的图像,三位同学分别说出了它的一些特点:
甲:对称轴为直线;
乙:与轴两个交点的横坐标都是整数;
丙:与轴交点的纵坐标也是整数,且以这三个点为顶点的三角形面积为3.请你写出满足上述全部特点的一个二次函数解析式__________________.
三、解答题(共60分)
21.(6分)已知二次函数的图像经过点、,对称轴为,求这个函数的解析式.
22.(6分)如图,AB是⊙O的直径,AC是弦,CD是⊙O的切 线,C为切点,AD⊥CD于点D.
求证:(1)∠AOC=2∠ACD;
(2)AC2=AB·AD.
第22题图
23.(6分)炮弹的运行轨道若不计空气阻力是一条抛物线.现测得我军炮位A与射击目标B的水平距离为600 m,炮弹运行的最大高度为1 200 m.
(1)求此抛物线的解析式.
(2)若在A、B之间距离A点500 m处有一高350 m的障碍物,计算炮弹能否越过障碍物.
24.(7分)某商店进行促销活动,如果将进价为8元的商品按每件10元出售,每天可销售100件,现采用提高售价,减少进货量的办法增加利润,已知这种商品每涨价1元,其销售量就要减少10件,问将售价定为多少元时,才能使每天所赚的利润最大?并求出最大利润.
25.(7分)(2013 湖北黄冈中考)某公司生产的一种健身产品在市场上受到普遍欢迎,每年可在国内、国外市场上全部售完,该公司的年产量为6千件,若在国内市场销售,平均每件产品的利润(元)与国内销售数量(千件)的关系为:若在国外销售,平均每件产品的利润(元)与国外的销售数量(千件)的关系为:
(1)用的代数式表示为=__________;
当时,与的函数解析式为=___________;
当_______时,
(2)求每年该公司销售这种健身产品的总利润(千元)与国内的销售数量(千件)的函数解析式,并指出的取值范围.
(3)该公司每年国内、国外的销售量各为多少时,可使公司每年的总利润最大?最大值为多少?
26.(7分)如图,在△ABC中,∠C= 90°,以AB上一点O为圆心,OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F.
(1)若AC=6,AB= 10,求⊙O的半径;
(2)连接OE、ED、DF、EF.若四边形BDEF是平行四边形,试判断四边形OFDE的形状,并说明理由.
27.(7分)如图,一位运动员在距篮圈下4米处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.
(1)建立如图所示的直角坐标系,求抛物线的解析式;
(2)已知该运动员身高1.8米,在这次跳投中,球在头顶上方0.25米处出手,问:球出手时,他跳离地面的高度是多少?
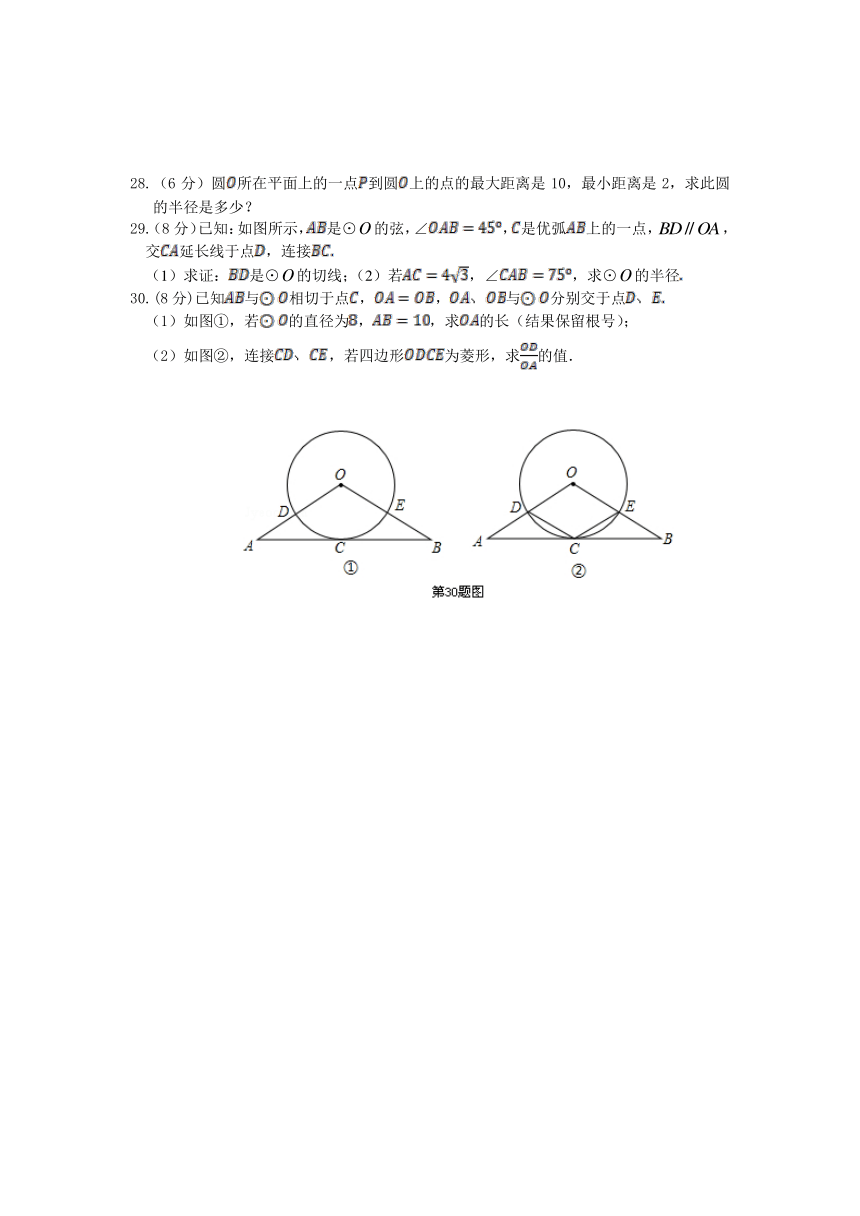
28.(6分)圆所在平面上的一点到圆上的点的最大距离是10,最小距离是2,求此圆的半径是多少?
29.(8分)已知:如图所示,是⊙的弦,∠,是优弧上的一点,,交延长线于点,连接
(1)求证:是⊙的切线;(2)若,∠,求⊙的半径
30.(8分)已知与相切于点,,与分别交于点
(1)如图①,若的直径为,,求的长(结果保留根号);
(2)如图②,连接,若四边形为菱形,求的值.
期中检测题参考答案
1.B 解析:选项A中过一点的圆的圆心不可以是点;选项C中只有当三点不共线时才有圆;选项D中过四点的圆不一定存在.只有B选项正确.
2.D 解析:二次函数与轴有两个交点,则所以选项B错误.二次函数图象的开口方向可能向上,也可能向下,所以选项A错误.符合条件的点有多种可能,当时,;当时,有两种情况:一种是,另一种是,所以选项C错误.而当时,,所以;当时,无论还是,都小于0,所以选项D正确.
3.D 解析:两圆相交或相切.
4.D 解析:在△中,∠°,,所以
过点则的半径长为.
5.D 解析:∵ =8 cm,⊙以1 cm/s的速度沿直线l向右运动,7 s后停止运动,∴ 7 s后两圆的圆心距为1 cm,两圆的半径的差为3-2=1(cm),∴ 此时两圆内切,
∴ 移动过程中没有内含这种位置关系,故选D.
6.C 解析:当时,二次函数图像开口向下,一次函数图像经过第二、四象限,此时C,D符合,又由二次函数的对称轴在轴左侧,所以,即,只有C符合.同理可讨论当时的情况.
7.B 解析: 抛物线的顶点坐标是(),
所以,解得.
8.D 解析:由于函数图像开口向下,所以在对称轴左侧随的增大而增大,由对称轴为,知的取值范围是.
9.D 解析:当时,,故抛物线经过固定点(1,3).
10.D 解析:画出抛物线简图可以看出,所以.
11.D 解析:由于已知两点的纵坐标相同,所以横坐标应关于对称轴对称,从而抛物线的对称轴为.
12.A 解析:当时,解得,从而所用时间为(s).
13.三角形的内部 三角形的斜边的中点 三角形的外部
14. 解析:∵ 是的切线,为的直径,∴ .
∴ .∵ ,∴ .
又∵ ,切于点.∴.∴为等边三角形.
∴.
15.相交 解析:将方程化为,解得,.
∵ ∴ ,∴ 和相交.
16. 解析:因为当时,, 当时,,所以.
17.(5,-2)
18. 解析:令,令,得,
因为,
所以△的面积是.
19.
20.本题答案不唯一,只要符合题意即可,如
21.解:因为二次函数的对称轴为,所以设函数的解析式为,
将点 、代入解析式,得解得
所以函数的解析式为.
22. 证明:(1)∵ CD是⊙O的切线,∴ ∠OCD=90°, 即∠ACD+∠ACO=90°.…①
∵ OC=OA,∴ ∠ACO=∠CAO,
∴ ∠AOC=180°-2∠ACO,即∠AOC+∠ACO=90°. ②
由①②,得∠ACD-∠AOC=0,即∠AOC=2∠ACD;
(2)如图,连接BC.
∵ AB是直径,∴ ∠ACB=90°.
在Rt△ACD与Rt△ABC中,∵ ∠AOC=2∠B,∴ ∠B=∠ACD,
∴ Rt△ACD∽Rt△ABC,∴ ,即AC2=AB·AD.
第22题答图
23.解:(1)建立直角坐标系,设点A为原点,则抛物线过点(0,0),(600,0),
从而抛物线的对称轴为.
又抛物线的最高点的纵坐标为1 200,则其顶点坐标为(300,1 200),
所以设抛物线的解析式为,
将(0,0)代入得,
所以抛物线的解析式为.
(2)将代入解析式,得,
所以炮弹能越过障碍物.
24. 解:设售价定为元.
由题意得,,
∵ ,∴ 当时,有最大值360.
答:将售价定为14元时,才能使每天所赚的利润最大,最大利润是360元.
25.解:(1)
(2)当时,
当时,
当时,
所以
(3)当时,
当时,
当时,
综上可知,当x=4时,
所以国内销售4千件,国外销售2千件时,最大利润为64万元(或640千元).
26. 解:(1)连接OD. 设⊙O的半径为
∵ BC切⊙O于点D,∴ OD⊥BC.
∵ ∠C=90°,∴ OD∥AC,∴ △OBD∽△ABC.
∴ = ,即 = . 解得r = ,
∴ ⊙O的半径为.
(2)四边形OFDE是菱形.
如图,连接OD,
∵ 四边形BDEF是平行四边形,∴ ∠DEF=∠B.
∵ ∠DEF=∠DOB,∴ ∠B=∠DOB.
∵ ∠ODB=90°,∴ ∠DOB+∠B=90°,∴ ∠DOB=60°.
∵DE∥AB,∴∠ODE=60°.
∵ OD=OE,∴ △ODE是等边三角形, ∴ OD=DE.
∵ OD=OF,∴ DE=OF.
∴ 四边形OFDE是平行四边形.
∵ OE=OF,∴ 平行四边形OFDE是菱形.
27.分析:(1)由函数的图像可设抛物线的解析式为,依题意可知图像经过的点的坐标,由此可得的值,进而求出抛物线的表达式.
(2)当时,,从而可求得他跳离地面的高度.
解:(1)设抛物线的解析式为.
由图像可知抛物线过点(0,3.5),(1.5,3.05),
所以解得
所以抛物线的解析式为.
(2)当时,,
所以球出手时,他跳离地面的高度是(米).
28.解:如图,分两种情况:
(1)当点为圆内一点时,过点作圆直径,分别交圆于点,由题意可得,,所以圆的半径为.
(2)当点在圆外时,作直线,分别交圆于点,由题意可得,,所以圆的半径为.
综上所述,所求圆的半径为6或4.
29. (1)证明:连接则∠∠.
因为∥,所以∠∠,所以∠,所以是⊙的切线
(2)解:因为∠,∠,所以∠ .
延长交于点连接∠
在Rt△,∠,所以所以⊙的半径为
30.解:(1)如图①,连接,则.
∵ 与相切于点,∴ .
在△中,∵ ,,∴ .
在Rt△中,由勾股定理,得.
(2)如图②,连接,则.
∵ 四边形为菱形,∴,
∴ △为等边三角形,有.
由(1)知,,∴ ,
∴ ,∴
第26题图
O
B
A
C
D
第29题图
第26题答图
A
B
O
P
A
B
O
P
第27题答图
(本检测题满分:120分,时间:120分钟)
一、选择题(每小题3分,共36分)
1.下列说法正确的是( )
A.过一点的圆的圆心可以是平面上任意点
B.过两点的圆的圆心在一条直线上
C.过三点的圆的圆心有且只有一点
D.过四点的圆不存在
2.(2013 江西中考)若二次函数的图像与轴有两个交点,坐标分别为且图像上有一点在轴下方,则下列判断正确的 是( )
A. B.
C. D.
3.已知两圆的半径分别为,且这两圆有公共点,则这两圆的圆心距为( )
A.4 B.10 C.4或10 D.
4.在△中,∠°,,以为圆心作和相切,则的半径长为( )
A.8 B.4 C.9.6 D.4.8
5.(2013 南京中考)如图,⊙、⊙的圆心、在直线l上,⊙的半径为2 cm,⊙的半径为3 cm,=8 cm.⊙以1 cm/s的速度沿直线l向右运动,7 s后停止运动.在此过程中,⊙与⊙没有出现的位置关系是( )
A.外切 B.相交 C.内切 D.内含
第5题图
6.一次函数与二次函数在同一坐标系中的图像可能是( )
7.已知抛物线的顶点坐标是,则和的值分别是( )
A.2,4 B. C.2, D.,0
8.对于函数,使得随的增大而增大的的取值范围是( )
A. B. C. D.
9.对于任意实数,抛物线 总经过一个固定的点,这个点是( )
A. (1, 0) B.(, 0) C.(, 3) D. (1, 3)
10.已知抛物线经过原点和第一、二、三象限,那么( )
A. B.
C. D.
11.若(2, 5)、(4, 5)是抛物线上的两点,则它的对称轴是( )
A. B. C. D.
12.小敏在今年的校运动会跳远比赛中跳出了满意一跳,函数(的单位:s,的单位:m)可以描述他跳跃时重心高度的变化.则他起跳后到重心最高时所用的时间
是( )
A.0.71 s B.0.70 s C.0.63 s D.0.36 s
二、填空题(每小题3分,共24分)
13.锐角三角形的外心在__________;直角三角形的外心在__________;钝角三角形的外心
在___________.
14.如图,已知为的直径,是的切线,为切点,
,则的度数为______.
15.已知和的半径分别是一元二次方程的两根,
且则和的位置关系是_______.
16.对于二次函数,已知当由1增加到2时,函数值减少3,则常
数的值是 .
17.将抛物线向右平移2个单位后,再向下平移5个单位,所得抛物线的顶点坐标为_______.
18.设三点依次分别是抛物线与轴的交点以及与轴的两个交点,则△的面积是 .
19.函数写成的形式是________,其图像的顶点坐标是
_______,对称轴是__________.
20.有一个二次函数的图像,三位同学分别说出了它的一些特点:
甲:对称轴为直线;
乙:与轴两个交点的横坐标都是整数;
丙:与轴交点的纵坐标也是整数,且以这三个点为顶点的三角形面积为3.请你写出满足上述全部特点的一个二次函数解析式__________________.
三、解答题(共60分)
21.(6分)已知二次函数的图像经过点、,对称轴为,求这个函数的解析式.
22.(6分)如图,AB是⊙O的直径,AC是弦,CD是⊙O的切 线,C为切点,AD⊥CD于点D.
求证:(1)∠AOC=2∠ACD;
(2)AC2=AB·AD.
第22题图
23.(6分)炮弹的运行轨道若不计空气阻力是一条抛物线.现测得我军炮位A与射击目标B的水平距离为600 m,炮弹运行的最大高度为1 200 m.
(1)求此抛物线的解析式.
(2)若在A、B之间距离A点500 m处有一高350 m的障碍物,计算炮弹能否越过障碍物.
24.(7分)某商店进行促销活动,如果将进价为8元的商品按每件10元出售,每天可销售100件,现采用提高售价,减少进货量的办法增加利润,已知这种商品每涨价1元,其销售量就要减少10件,问将售价定为多少元时,才能使每天所赚的利润最大?并求出最大利润.
25.(7分)(2013 湖北黄冈中考)某公司生产的一种健身产品在市场上受到普遍欢迎,每年可在国内、国外市场上全部售完,该公司的年产量为6千件,若在国内市场销售,平均每件产品的利润(元)与国内销售数量(千件)的关系为:若在国外销售,平均每件产品的利润(元)与国外的销售数量(千件)的关系为:
(1)用的代数式表示为=__________;
当时,与的函数解析式为=___________;
当_______时,
(2)求每年该公司销售这种健身产品的总利润(千元)与国内的销售数量(千件)的函数解析式,并指出的取值范围.
(3)该公司每年国内、国外的销售量各为多少时,可使公司每年的总利润最大?最大值为多少?
26.(7分)如图,在△ABC中,∠C= 90°,以AB上一点O为圆心,OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F.
(1)若AC=6,AB= 10,求⊙O的半径;
(2)连接OE、ED、DF、EF.若四边形BDEF是平行四边形,试判断四边形OFDE的形状,并说明理由.
27.(7分)如图,一位运动员在距篮圈下4米处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.
(1)建立如图所示的直角坐标系,求抛物线的解析式;
(2)已知该运动员身高1.8米,在这次跳投中,球在头顶上方0.25米处出手,问:球出手时,他跳离地面的高度是多少?
28.(6分)圆所在平面上的一点到圆上的点的最大距离是10,最小距离是2,求此圆的半径是多少?
29.(8分)已知:如图所示,是⊙的弦,∠,是优弧上的一点,,交延长线于点,连接
(1)求证:是⊙的切线;(2)若,∠,求⊙的半径
30.(8分)已知与相切于点,,与分别交于点
(1)如图①,若的直径为,,求的长(结果保留根号);
(2)如图②,连接,若四边形为菱形,求的值.
期中检测题参考答案
1.B 解析:选项A中过一点的圆的圆心不可以是点;选项C中只有当三点不共线时才有圆;选项D中过四点的圆不一定存在.只有B选项正确.
2.D 解析:二次函数与轴有两个交点,则所以选项B错误.二次函数图象的开口方向可能向上,也可能向下,所以选项A错误.符合条件的点有多种可能,当时,;当时,有两种情况:一种是,另一种是,所以选项C错误.而当时,,所以;当时,无论还是,都小于0,所以选项D正确.
3.D 解析:两圆相交或相切.
4.D 解析:在△中,∠°,,所以
过点则的半径长为.
5.D 解析:∵ =8 cm,⊙以1 cm/s的速度沿直线l向右运动,7 s后停止运动,∴ 7 s后两圆的圆心距为1 cm,两圆的半径的差为3-2=1(cm),∴ 此时两圆内切,
∴ 移动过程中没有内含这种位置关系,故选D.
6.C 解析:当时,二次函数图像开口向下,一次函数图像经过第二、四象限,此时C,D符合,又由二次函数的对称轴在轴左侧,所以,即,只有C符合.同理可讨论当时的情况.
7.B 解析: 抛物线的顶点坐标是(),
所以,解得.
8.D 解析:由于函数图像开口向下,所以在对称轴左侧随的增大而增大,由对称轴为,知的取值范围是.
9.D 解析:当时,,故抛物线经过固定点(1,3).
10.D 解析:画出抛物线简图可以看出,所以.
11.D 解析:由于已知两点的纵坐标相同,所以横坐标应关于对称轴对称,从而抛物线的对称轴为.
12.A 解析:当时,解得,从而所用时间为(s).
13.三角形的内部 三角形的斜边的中点 三角形的外部
14. 解析:∵ 是的切线,为的直径,∴ .
∴ .∵ ,∴ .
又∵ ,切于点.∴.∴为等边三角形.
∴.
15.相交 解析:将方程化为,解得,.
∵ ∴ ,∴ 和相交.
16. 解析:因为当时,, 当时,,所以.
17.(5,-2)
18. 解析:令,令,得,
因为,
所以△的面积是.
19.
20.本题答案不唯一,只要符合题意即可,如
21.解:因为二次函数的对称轴为,所以设函数的解析式为,
将点 、代入解析式,得解得
所以函数的解析式为.
22. 证明:(1)∵ CD是⊙O的切线,∴ ∠OCD=90°, 即∠ACD+∠ACO=90°.…①
∵ OC=OA,∴ ∠ACO=∠CAO,
∴ ∠AOC=180°-2∠ACO,即∠AOC+∠ACO=90°. ②
由①②,得∠ACD-∠AOC=0,即∠AOC=2∠ACD;
(2)如图,连接BC.
∵ AB是直径,∴ ∠ACB=90°.
在Rt△ACD与Rt△ABC中,∵ ∠AOC=2∠B,∴ ∠B=∠ACD,
∴ Rt△ACD∽Rt△ABC,∴ ,即AC2=AB·AD.
第22题答图
23.解:(1)建立直角坐标系,设点A为原点,则抛物线过点(0,0),(600,0),
从而抛物线的对称轴为.
又抛物线的最高点的纵坐标为1 200,则其顶点坐标为(300,1 200),
所以设抛物线的解析式为,
将(0,0)代入得,
所以抛物线的解析式为.
(2)将代入解析式,得,
所以炮弹能越过障碍物.
24. 解:设售价定为元.
由题意得,,
∵ ,∴ 当时,有最大值360.
答:将售价定为14元时,才能使每天所赚的利润最大,最大利润是360元.
25.解:(1)
(2)当时,
当时,
当时,
所以
(3)当时,
当时,
当时,
综上可知,当x=4时,
所以国内销售4千件,国外销售2千件时,最大利润为64万元(或640千元).
26. 解:(1)连接OD. 设⊙O的半径为
∵ BC切⊙O于点D,∴ OD⊥BC.
∵ ∠C=90°,∴ OD∥AC,∴ △OBD∽△ABC.
∴ = ,即 = . 解得r = ,
∴ ⊙O的半径为.
(2)四边形OFDE是菱形.
如图,连接OD,
∵ 四边形BDEF是平行四边形,∴ ∠DEF=∠B.
∵ ∠DEF=∠DOB,∴ ∠B=∠DOB.
∵ ∠ODB=90°,∴ ∠DOB+∠B=90°,∴ ∠DOB=60°.
∵DE∥AB,∴∠ODE=60°.
∵ OD=OE,∴ △ODE是等边三角形, ∴ OD=DE.
∵ OD=OF,∴ DE=OF.
∴ 四边形OFDE是平行四边形.
∵ OE=OF,∴ 平行四边形OFDE是菱形.
27.分析:(1)由函数的图像可设抛物线的解析式为,依题意可知图像经过的点的坐标,由此可得的值,进而求出抛物线的表达式.
(2)当时,,从而可求得他跳离地面的高度.
解:(1)设抛物线的解析式为.
由图像可知抛物线过点(0,3.5),(1.5,3.05),
所以解得
所以抛物线的解析式为.
(2)当时,,
所以球出手时,他跳离地面的高度是(米).
28.解:如图,分两种情况:
(1)当点为圆内一点时,过点作圆直径,分别交圆于点,由题意可得,,所以圆的半径为.
(2)当点在圆外时,作直线,分别交圆于点,由题意可得,,所以圆的半径为.
综上所述,所求圆的半径为6或4.
29. (1)证明:连接则∠∠.
因为∥,所以∠∠,所以∠,所以是⊙的切线
(2)解:因为∠,∠,所以∠ .
延长交于点连接∠
在Rt△,∠,所以所以⊙的半径为
30.解:(1)如图①,连接,则.
∵ 与相切于点,∴ .
在△中,∵ ,,∴ .
在Rt△中,由勾股定理,得.
(2)如图②,连接,则.
∵ 四边形为菱形,∴,
∴ △为等边三角形,有.
由(1)知,,∴ ,
∴ ,∴
第26题图
O
B
A
C
D
第29题图
第26题答图
A
B
O
P
A
B
O
P
第27题答图
同课章节目录
