第十七章 勾股定理 章末复习(47张ppt)
文档属性
| 名称 | 第十七章 勾股定理 章末复习(47张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-15 00:00:00 | ||
图片预览








文档简介
(共47张PPT)
章末复习
R·八年级数学下册
复习导入
本章我们学习了什么内容?
那么大家掌握得如何呢?这节课我们一起来作一个回顾总结,检阅学习成果.
想一想
勾股定理及勾股定理的逆定理.
复习目标
1.复习与回顾本章的重要知识点和知识结构.
2.总结本章的重要思想方法及其应用.
分层复习
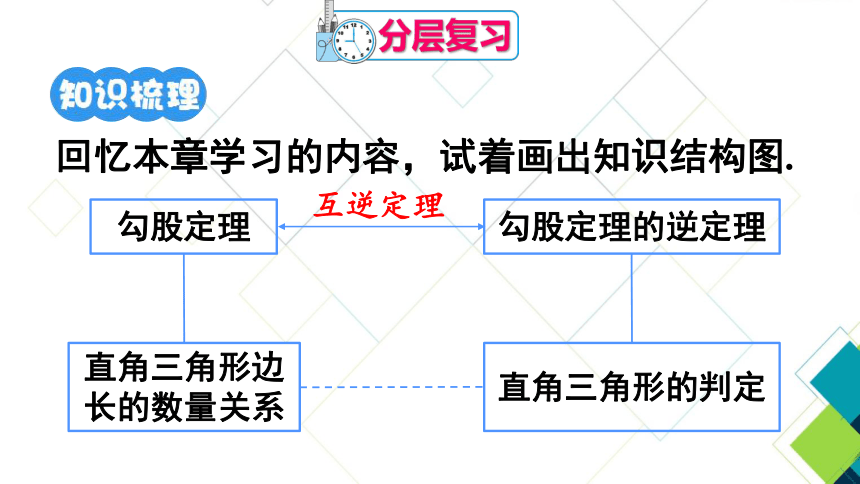
回忆本章学习的内容,试着画出知识结构图.
勾股定理
勾股定理的逆定理
互逆定理
直角三角形边长的数量关系
直角三角形的判定
如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
直角三角形三边的长有什么特殊的关系?
问题
1
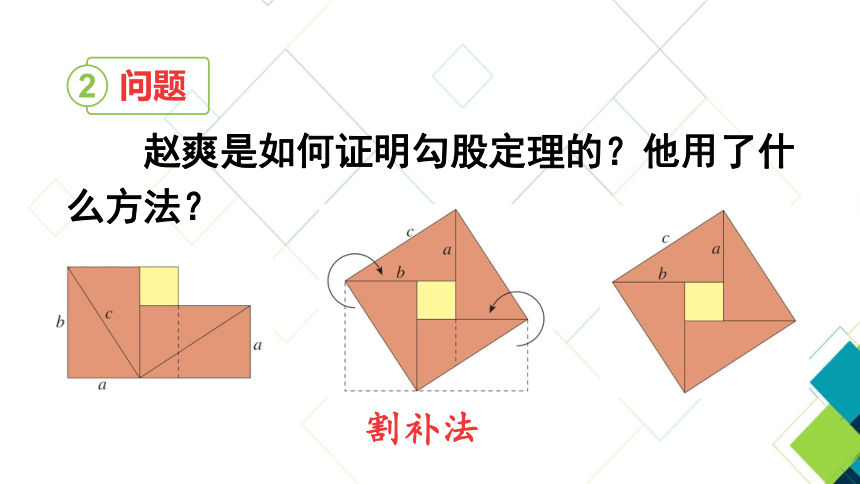
赵爽是如何证明勾股定理的?他用了什么方法?
问题
2
割补法
已知一个三角形的三边长,怎样判断它是不是直角三角形?你判断的依据是什么?
问题
3
如果三角形ABC的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形;
勾股定理的逆定理.
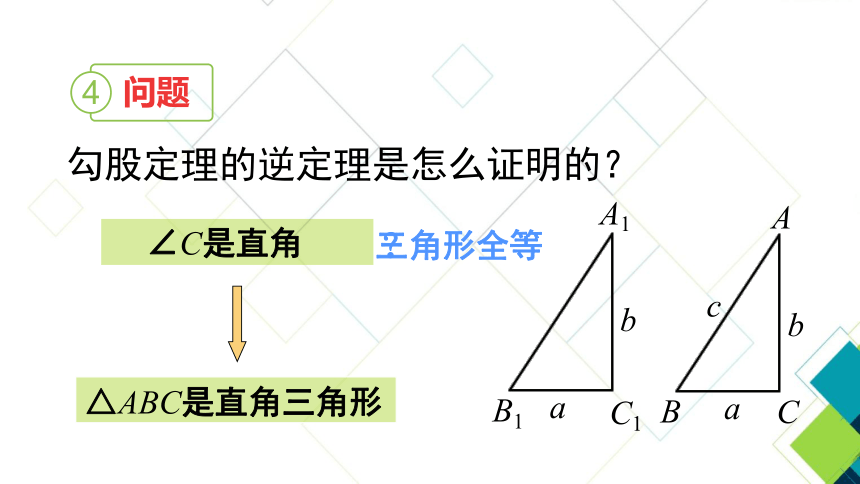
勾股定理的逆定理是怎么证明的?
问题
4
A1
B1
C1
?
三角形全等
∠C是直角
△ABC是直角三角形
A
B
C
a
b
c
a
问题
5
一个命题成立,它的逆命题一定成立吗?请举例说明.
不一定;如“如果两个角是直角,那么它们相等”,其逆命题为“如果两个角相等,那么这两个角是直角”,是假命题.
典例解析
例1 下列各组数中,不是勾股数的是( )
A.4,3,5 B.5,12,13
C.10,15,18 D.8,15,17
解析 能构成为直角三角形三条边长的三个正整数称为勾股数.
C
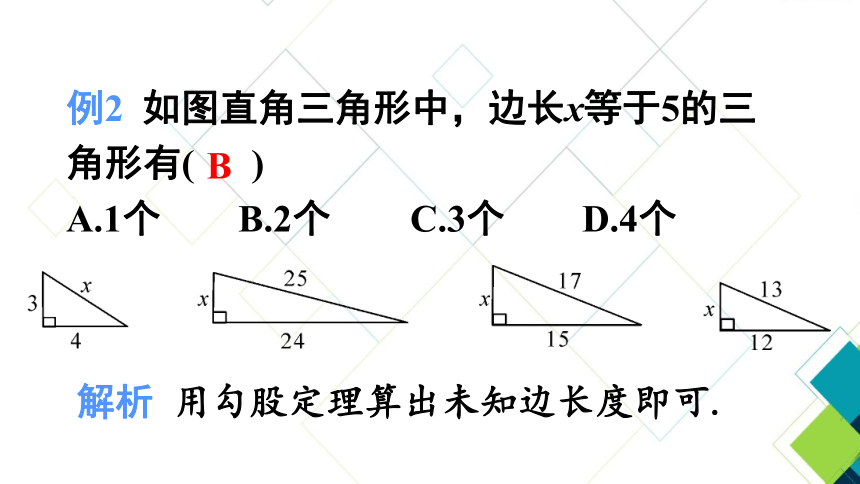
例2 如图直角三角形中,边长x等于5的三角形有( )
A.1个 B.2个 C.3个 D.4个
解析 用勾股定理算出未知边长度即可.
B
例3 一束光线从y轴上点A(0, 1)出发,经过x轴上点C反射后经过点B(3, 3),则光线从A点到B点经过的路线长是 .
解析 作辅助线,利用入射角等于反射角可构建相似三角形,再进行计算.
5
例4 我国古代数学家赵爽的“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边分别为a、b,那么(a+b)2的值是 .
解析 大正方形的面积=c2,小正方形的面积=(a-b)2.
25
例5 如图,在梯形ABCD中,AB∥CD,∠A=
90°, AB=2,BC=3,CD=1,E是AD中点.求证:CE⊥BE.
解析 如图,作辅助线,求出各边长度,借助勾股定理的逆定理给出证明.
证明 ∵CF⊥AB,AB∥CD,∠A=90°,
∴四边形ADCF为矩形.
∴FB=AB-AF=2-1=1.
∴CE⊥BE.
例6 如图,一个圆柱形油罐,要从A点环绕油罐建梯子,正好到A点的正上方B点,请你算一算梯子最短需多少米?(已知油罐的底面周长是12米,高是5米)
解析 将油罐沿AB切开铺平,对角线为最短路线.
解:如图,将油罐侧面展开,
随堂演练
基础巩固
1.如图,为求出湖两岸的A、B两点之间的距离,一个观测者在点C设桩,使△ABC恰好为直角三角形,且∠B=90°,再测得AC长160米,BC长128米,则A、B之间的距离为( )
A.96米 B.100米
C.86米 D.90米
A
2.下列命题中,逆命题仍然成立的是( )
A.全等三角形的面积相等
B.到角两边距离相等的点在这个角的平分线上
C.同一个角的余角相等
D.等腰三角形是轴对称图形
B
综合应用
7. 如图所示,一只蚂蚁在A处往东爬8格后,又向北爬2格,遇到干扰后又向西爬3格,再折向北爬6格,这时发现B处有食物,于是便又向东爬1格到B处找到食物,如果图中每一个方格都是边长为1cm的正方形,问此时蚂蚁爬行的路程是多少?如果蚂蚁从A处沿直线AB到达B处,则可少爬多远的路程?
解:此时蚂蚁爬行的路程是:8+2+3+6+1=20(cm),
若蚂蚁从A处沿直线AB到达B处;设由A向东6格处的点为C(如图所示),
易知△ABC为直角三角形,
20-10=10(cm).
则可少爬10cm.
拓展延伸
如图,已知B、C两个乡镇相距25千米,有一个自然保护区A与B相距15千米,A与C相距20千米,以点A为圆心,10千米为半径是自然保护区的范围,现在要在B、C两个乡镇之间修一条笔直的公路,请问:这条公路是否会穿过自然保护区?试通过计算加以说明.
解:如图,过点A作AD⊥BC交BC于点D.
在△ABC中,AB2+AC2=152+202=252=BC2.
∴△ABC为直角三角形,∠BAC=90°.
又∵AB·AC=AD·BC.
∴这条公路不会穿过自然保护区.
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
复习题17
1.两人从同一地点同时出发,一人以20m/min
的速度向北直行,一人以30 m/min的速度向东直行.10 min后他们相距多远(结果取整数)?
复习巩固
BC=10×30=300(米),
连AB,在Rt△ABC中,由勾股定理
所以10分钟后他们相距约为361米.
解:如图,设两人从C点出发,10分钟后分别到达A、B两点,依据题意有:
∠C=90°,AC=10×20=200(米),
2.如图,过圆锥的顶点S和底面圆的圆心O的平面截圆锥得截面△SAB,其中SA=SB,AB是圆锥底面圆O的直径.已知SA=7 cm,AB=4 cm,求截面△SAB的面积.
解:由勾股定理得
则
则
3.如图,车床齿轮箱壳要钻两个圆孔,两孔中心的距离是134 mm,两孔中心的水平距离是77 mm.计算两孔中心的垂直距离(结果保留小数点后一位).
解:在Rt△ABC中,AB=134mm,BC=77mm,
由勾股定理得,
所以两孔中心的垂直距离约为109.7mm.
4.如图,要修一个育苗棚,棚的横截面是直角三角形,棚宽a=3 m,高b=1.5 m,长d=10 m.求覆盖在顶上的塑料薄膜需多少平方米(结果保留小数点后一位).
解:由勾股定理得,棚顶的宽为:
则棚顶的面积为3.35×10=33.5(m2)
所以覆盖在顶上塑料薄膜需33.5平方米.
5.一个三角形三边的比为1∶ ∶2,这个三角形是直角三角形吗?
解:这个三角形是直角三角形.
理由:因为这个三角形三边的比为1∶ ∶2,因此不妨设这个三角形的三边为k, k,2k(其中k>0),因为k2+( k)2=(2k)2,由勾股定理的逆定理知,这个三角形是直角三角形.
6.下列各命题都成立,写出它们的逆命题.这些逆命题成立吗?
(1)两条直线平行,同位角相等;
(2)如果两个实数都是正数,那么它们的积是正数;
(3)等边三角形是锐角三角形;
(4)线段垂直平分线上的点到这条线段两个端点的距离相等.
解:(1)逆命题:同位角相等,两直线平行;成立.
(2)逆命题:如果两个实数的积是正数,那么这两个实数都是正数;不成立.
(3)逆命题:锐角三角形是等边三角形;不成立.
(4)逆命题:到线段两个端点距离相等的点在这条线段的垂直平分线上;成立.
7.已知直角三角形的两条直角边的长分别为2 +1和2 -1,求斜边c的长.
解:根据勾股定理:
8.如图,在△ABC中,AB=AC=BC,高AD=h.求AB.
综合应用
解:设AB长为x.
∵AB=AC=BC,AD⊥BC,∠BAD=30°,
∴BD=DC= x,
由勾股定理得:AB2=BD2+AD2,即
x2= +h2,∴x= h.
9.如图,每个小正方形的边长都为1.
(1)求四边形ABCD的面积与周长;
(2)∠BCD是直角吗?
解:(1)
所以四边形ABCD周长为AB+BC+CD+AD=15.93.
(2)∠BCD是直角.
因为由勾股定理得BD=5,由(1)知CD= BC
= ,因此在△BCD中,BD2=25,CD2+BC2=25,即BD2=CD2+BC2,所以△BCD是直角三角形,且∠BCD为直角.
10.一根竹子高1丈,折断后竹子顶端落在离竹子底端3尺处.折断处离地面的高度是多少?(这是我国古代数学著作《九章算术》中的一个问题.其中的丈、尺是长度单位,1丈=10尺.)
解:折断的竹子与地面上所在的线段构成直角三角形,设折断处距地面的高度为x尺,根据勾股定理可得方程:
x2+32=(10-x)2,
解这个方程得x=4.55.
所以折断处离地面的高度为4.55尺.
11.古希腊的哲学家柏拉图曾指出,如果m表示大于1的整数,a=2m,b=m2-1,c=m2+1,那么a,b,c为勾股数.你认为对吗?如果对,你能利用这个结论得出一些勾股数吗?
解:对;
∵a2=(2m)2=4m2,
b2=(m2-1)2=m4-2m2+1,
c2=(m2+1)2=m4+2m2+1,
a2+b2=4m2+m4-2m2+1=m4+2m2+1=c2,
∴a、b、c为勾股数.
例:20,99,101;10,24,26.
拓广探索
12.如图,圆柱的底面半径为6 cm,高为10 cm,蚂蚁在圆柱表面爬行,从点A爬到点B的最短路程是多少厘米(结果保留小数点后一位)?
解:由两点之间,直线最短易知,蚂蚁沿侧面展开后AB的连线爬行,路程最短.
将侧面展开成如图所示的矩形ACDE,则B恰是CD的中点,连AB,在Rt△ACB中,AC=10(cm),
故蚂蚁爬行的最短路程约为21.3cm.
CB= ×2×6π=6π(cm),
由勾股定理得:
13.一根70 cm的木棒,要放在长、宽、高分别是50 cm,40 cm,30 cm的长方体木箱中,能放进去吗?(提示:长方体的高垂直于底面的任何一条直线.)
解:如图所示,长方体木箱能放进木棒的最大长度应为对角线DC的长.
连DC、AC则AD⊥AC,即∠DAC=90°,
在Rt△ABC中,∠ABC=90°,AB=50,BC=40.
由勾股定理得:
在Rt△ADC中,由勾股定理得:
所以能放进去.
14.设直角三角形的两条直角边长及斜边上的高分
别为a,b及h.求证: .
证明:设斜边长为c,由直角三角形面积公式可知:
章末复习
R·八年级数学下册
复习导入
本章我们学习了什么内容?
那么大家掌握得如何呢?这节课我们一起来作一个回顾总结,检阅学习成果.
想一想
勾股定理及勾股定理的逆定理.
复习目标
1.复习与回顾本章的重要知识点和知识结构.
2.总结本章的重要思想方法及其应用.
分层复习
回忆本章学习的内容,试着画出知识结构图.
勾股定理
勾股定理的逆定理
互逆定理
直角三角形边长的数量关系
直角三角形的判定
如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
直角三角形三边的长有什么特殊的关系?
问题
1
赵爽是如何证明勾股定理的?他用了什么方法?
问题
2
割补法
已知一个三角形的三边长,怎样判断它是不是直角三角形?你判断的依据是什么?
问题
3
如果三角形ABC的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形;
勾股定理的逆定理.
勾股定理的逆定理是怎么证明的?
问题
4
A1
B1
C1
?
三角形全等
∠C是直角
△ABC是直角三角形
A
B
C
a
b
c
a
问题
5
一个命题成立,它的逆命题一定成立吗?请举例说明.
不一定;如“如果两个角是直角,那么它们相等”,其逆命题为“如果两个角相等,那么这两个角是直角”,是假命题.
典例解析
例1 下列各组数中,不是勾股数的是( )
A.4,3,5 B.5,12,13
C.10,15,18 D.8,15,17
解析 能构成为直角三角形三条边长的三个正整数称为勾股数.
C
例2 如图直角三角形中,边长x等于5的三角形有( )
A.1个 B.2个 C.3个 D.4个
解析 用勾股定理算出未知边长度即可.
B
例3 一束光线从y轴上点A(0, 1)出发,经过x轴上点C反射后经过点B(3, 3),则光线从A点到B点经过的路线长是 .
解析 作辅助线,利用入射角等于反射角可构建相似三角形,再进行计算.
5
例4 我国古代数学家赵爽的“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边分别为a、b,那么(a+b)2的值是 .
解析 大正方形的面积=c2,小正方形的面积=(a-b)2.
25
例5 如图,在梯形ABCD中,AB∥CD,∠A=
90°, AB=2,BC=3,CD=1,E是AD中点.求证:CE⊥BE.
解析 如图,作辅助线,求出各边长度,借助勾股定理的逆定理给出证明.
证明 ∵CF⊥AB,AB∥CD,∠A=90°,
∴四边形ADCF为矩形.
∴FB=AB-AF=2-1=1.
∴CE⊥BE.
例6 如图,一个圆柱形油罐,要从A点环绕油罐建梯子,正好到A点的正上方B点,请你算一算梯子最短需多少米?(已知油罐的底面周长是12米,高是5米)
解析 将油罐沿AB切开铺平,对角线为最短路线.
解:如图,将油罐侧面展开,
随堂演练
基础巩固
1.如图,为求出湖两岸的A、B两点之间的距离,一个观测者在点C设桩,使△ABC恰好为直角三角形,且∠B=90°,再测得AC长160米,BC长128米,则A、B之间的距离为( )
A.96米 B.100米
C.86米 D.90米
A
2.下列命题中,逆命题仍然成立的是( )
A.全等三角形的面积相等
B.到角两边距离相等的点在这个角的平分线上
C.同一个角的余角相等
D.等腰三角形是轴对称图形
B
综合应用
7. 如图所示,一只蚂蚁在A处往东爬8格后,又向北爬2格,遇到干扰后又向西爬3格,再折向北爬6格,这时发现B处有食物,于是便又向东爬1格到B处找到食物,如果图中每一个方格都是边长为1cm的正方形,问此时蚂蚁爬行的路程是多少?如果蚂蚁从A处沿直线AB到达B处,则可少爬多远的路程?
解:此时蚂蚁爬行的路程是:8+2+3+6+1=20(cm),
若蚂蚁从A处沿直线AB到达B处;设由A向东6格处的点为C(如图所示),
易知△ABC为直角三角形,
20-10=10(cm).
则可少爬10cm.
拓展延伸
如图,已知B、C两个乡镇相距25千米,有一个自然保护区A与B相距15千米,A与C相距20千米,以点A为圆心,10千米为半径是自然保护区的范围,现在要在B、C两个乡镇之间修一条笔直的公路,请问:这条公路是否会穿过自然保护区?试通过计算加以说明.
解:如图,过点A作AD⊥BC交BC于点D.
在△ABC中,AB2+AC2=152+202=252=BC2.
∴△ABC为直角三角形,∠BAC=90°.
又∵AB·AC=AD·BC.
∴这条公路不会穿过自然保护区.
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
复习题17
1.两人从同一地点同时出发,一人以20m/min
的速度向北直行,一人以30 m/min的速度向东直行.10 min后他们相距多远(结果取整数)?
复习巩固
BC=10×30=300(米),
连AB,在Rt△ABC中,由勾股定理
所以10分钟后他们相距约为361米.
解:如图,设两人从C点出发,10分钟后分别到达A、B两点,依据题意有:
∠C=90°,AC=10×20=200(米),
2.如图,过圆锥的顶点S和底面圆的圆心O的平面截圆锥得截面△SAB,其中SA=SB,AB是圆锥底面圆O的直径.已知SA=7 cm,AB=4 cm,求截面△SAB的面积.
解:由勾股定理得
则
则
3.如图,车床齿轮箱壳要钻两个圆孔,两孔中心的距离是134 mm,两孔中心的水平距离是77 mm.计算两孔中心的垂直距离(结果保留小数点后一位).
解:在Rt△ABC中,AB=134mm,BC=77mm,
由勾股定理得,
所以两孔中心的垂直距离约为109.7mm.
4.如图,要修一个育苗棚,棚的横截面是直角三角形,棚宽a=3 m,高b=1.5 m,长d=10 m.求覆盖在顶上的塑料薄膜需多少平方米(结果保留小数点后一位).
解:由勾股定理得,棚顶的宽为:
则棚顶的面积为3.35×10=33.5(m2)
所以覆盖在顶上塑料薄膜需33.5平方米.
5.一个三角形三边的比为1∶ ∶2,这个三角形是直角三角形吗?
解:这个三角形是直角三角形.
理由:因为这个三角形三边的比为1∶ ∶2,因此不妨设这个三角形的三边为k, k,2k(其中k>0),因为k2+( k)2=(2k)2,由勾股定理的逆定理知,这个三角形是直角三角形.
6.下列各命题都成立,写出它们的逆命题.这些逆命题成立吗?
(1)两条直线平行,同位角相等;
(2)如果两个实数都是正数,那么它们的积是正数;
(3)等边三角形是锐角三角形;
(4)线段垂直平分线上的点到这条线段两个端点的距离相等.
解:(1)逆命题:同位角相等,两直线平行;成立.
(2)逆命题:如果两个实数的积是正数,那么这两个实数都是正数;不成立.
(3)逆命题:锐角三角形是等边三角形;不成立.
(4)逆命题:到线段两个端点距离相等的点在这条线段的垂直平分线上;成立.
7.已知直角三角形的两条直角边的长分别为2 +1和2 -1,求斜边c的长.
解:根据勾股定理:
8.如图,在△ABC中,AB=AC=BC,高AD=h.求AB.
综合应用
解:设AB长为x.
∵AB=AC=BC,AD⊥BC,∠BAD=30°,
∴BD=DC= x,
由勾股定理得:AB2=BD2+AD2,即
x2= +h2,∴x= h.
9.如图,每个小正方形的边长都为1.
(1)求四边形ABCD的面积与周长;
(2)∠BCD是直角吗?
解:(1)
所以四边形ABCD周长为AB+BC+CD+AD=15.93.
(2)∠BCD是直角.
因为由勾股定理得BD=5,由(1)知CD= BC
= ,因此在△BCD中,BD2=25,CD2+BC2=25,即BD2=CD2+BC2,所以△BCD是直角三角形,且∠BCD为直角.
10.一根竹子高1丈,折断后竹子顶端落在离竹子底端3尺处.折断处离地面的高度是多少?(这是我国古代数学著作《九章算术》中的一个问题.其中的丈、尺是长度单位,1丈=10尺.)
解:折断的竹子与地面上所在的线段构成直角三角形,设折断处距地面的高度为x尺,根据勾股定理可得方程:
x2+32=(10-x)2,
解这个方程得x=4.55.
所以折断处离地面的高度为4.55尺.
11.古希腊的哲学家柏拉图曾指出,如果m表示大于1的整数,a=2m,b=m2-1,c=m2+1,那么a,b,c为勾股数.你认为对吗?如果对,你能利用这个结论得出一些勾股数吗?
解:对;
∵a2=(2m)2=4m2,
b2=(m2-1)2=m4-2m2+1,
c2=(m2+1)2=m4+2m2+1,
a2+b2=4m2+m4-2m2+1=m4+2m2+1=c2,
∴a、b、c为勾股数.
例:20,99,101;10,24,26.
拓广探索
12.如图,圆柱的底面半径为6 cm,高为10 cm,蚂蚁在圆柱表面爬行,从点A爬到点B的最短路程是多少厘米(结果保留小数点后一位)?
解:由两点之间,直线最短易知,蚂蚁沿侧面展开后AB的连线爬行,路程最短.
将侧面展开成如图所示的矩形ACDE,则B恰是CD的中点,连AB,在Rt△ACB中,AC=10(cm),
故蚂蚁爬行的最短路程约为21.3cm.
CB= ×2×6π=6π(cm),
由勾股定理得:
13.一根70 cm的木棒,要放在长、宽、高分别是50 cm,40 cm,30 cm的长方体木箱中,能放进去吗?(提示:长方体的高垂直于底面的任何一条直线.)
解:如图所示,长方体木箱能放进木棒的最大长度应为对角线DC的长.
连DC、AC则AD⊥AC,即∠DAC=90°,
在Rt△ABC中,∠ABC=90°,AB=50,BC=40.
由勾股定理得:
在Rt△ADC中,由勾股定理得:
所以能放进去.
14.设直角三角形的两条直角边长及斜边上的高分
别为a,b及h.求证: .
证明:设斜边长为c,由直角三角形面积公式可知:
