八年级数学《勾股定理的应用》课件

课件15张PPT。八年级(上册)初中数学3.3　勾股定理的简单应用
把勾股定理送到外星
球，与外星人进行数学交流 ！
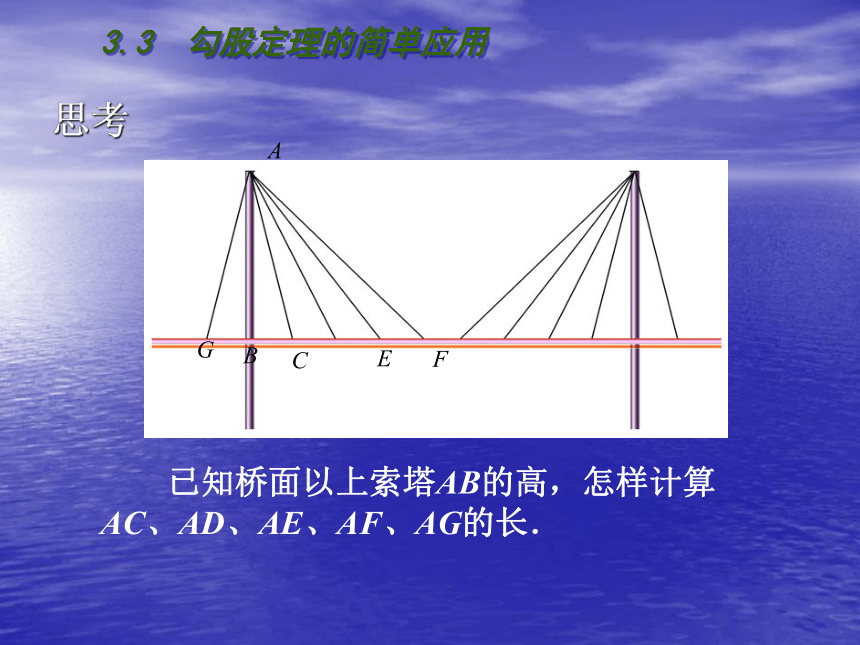
——华罗庚交流　　从远处看，斜拉桥的索塔、桥面与拉索组成许多直角三角形．3.3　勾股定理的简单应用思考　　已知桥面以上索塔AB的高，怎样计算AC、AD、AE、AF、AG的长．3.3　勾股定理的简单应用例1　九章算术中的“折竹”问题：今有竹高
一丈，末折抵地，去根三尺，问折者高几何？
　　意思是：有一根竹子原高1丈（1丈＝10尺），中部有一处折断，竹梢触地面处离竹根3尺，试问折断处离地面多高？3.3　勾股定理的简单应用解：如图，我们用线段OA和线段AB来表示竹子，其中线段AB表示竹子折断部分，用线段OB来表示竹梢触地处离竹根的距离．设OA＝x，则AB＝10－x．∵∠AOB＝90°，
∴OA2＋OB2＝AB2，
∴x2＋32＝（10－x）2．??3.3　勾股定理的简单应用．练习 　“引葭赴岸”是《九章算术》中
另一道题“今有池方一丈，葭生其中央，出
水一尺,引葭赴岸，适与岸齐．问水深、
葭长各几何？”
　　题意是：有一个边长为10尺的正方形池塘，在水
池正中央有一根新生的芦苇，它高出水面1尺，如果把
这根芦苇沿与水池边垂直的方向拉向岸边，它的顶端恰
好到达岸边．请问这个水池的深度和这根芦苇的长度各
是多少？3.3　勾股定理的简单应用解：如图， 　　BC为芦苇长，AB为水深，AC为池中心点距岸边的距离． 　　　　　设AB ＝x尺，
则BC ＝（ x ＋1）尺，
根据勾股定理得：
x2＋52＝(x＋1)2，
即：（x＋1）2－x2 ＝52，
解得：x＝12，
所以芦苇长为12＋1＝13（尺），
　答：水深为12尺，芦苇长为13尺．?3.3　勾股定理的简单应用 例2　如图，在△ABC中，
AB＝26，BC＝20，BC边上的
中线AD＝24，求AC. 3.3　勾股定理的简单应用∴BD＝CD＝ BC＝ ×20＝10．
∵AD2＋BD2＝576＋100＝676，
AB 2＝262＝676，www.12999.com议一议 勾股定理与它的逆定理在应用上有什么区别？ 　勾股定理主要应用于求线段的长度、图形的周长、面积；
　勾股定理的逆定理用于判断三角形的形状． 3.3　勾股定理的简单应用1．如图，在△ABC中， AB＝AC＝17，BC＝16，求△ABC的面积． 练一练3.3　勾股定理的简单应用2．如图，在△ABC中，AD⊥BC，AB＝15，
AD＝12，AC＝13，求△ABC的周长和面积． DCBA3.3　勾股定理的简单应用试一试 如图，以△ABC的三边为直径向外作半圆，且
S1＋S3＝S2，试判断△ABC的形状？ 3.3　勾股定理的简单应用小结　　从勾股定理的应用中我们进一步体会到直角
三角形与等腰三角形有着密切的联系；把研究等
腰三角形转化为研究直角三角形，这是研究问题
的一种策略． 3.3　勾股定理的简单应用谢 谢!