人教版数学九年级上册 24.2.1点和圆的位置关系 课件(共25张PPT)
文档属性
| 名称 | 人教版数学九年级上册 24.2.1点和圆的位置关系 课件(共25张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-13 18:59:29 | ||
图片预览









文档简介
(共25张PPT)
创设情景 明确目标
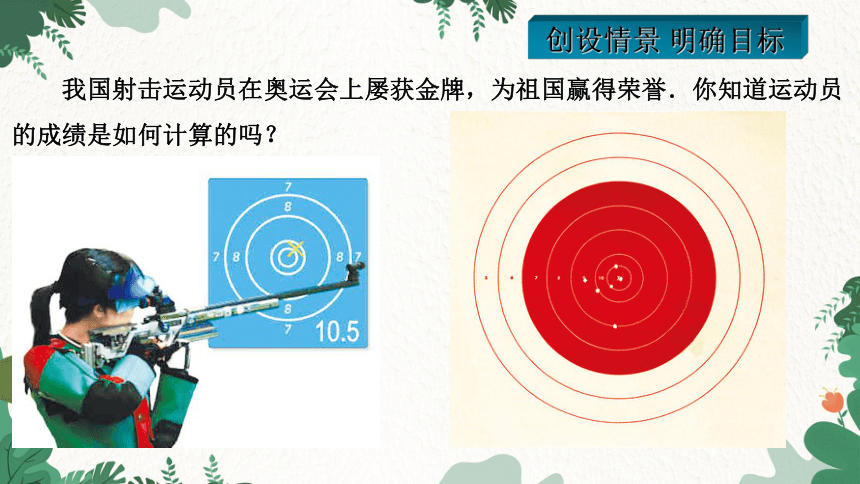
我国射击运动员在奥运会上屡获金牌,为祖国赢得荣誉.你知道运动员的成绩是如何计算的吗?
24.2.1 点和圆的位置关系
学习目标
(一)掌握点和圆的三种位置关系。
(二)了解不在同一直线上的三点确定一个圆,以及过不在同一条直线上的三个点作圆的方法;
(三)理解并掌握三角形的外接圆及三角形外心的概念。
我们是如何判断点与圆的位置关系的?
探究一:
r
问题2:设⊙O半径为r,说出来点A,点B,点C与圆心O的距离与半径的关系:
·
C
O
A
B
OC > r.
问题1:观察图中点A,点B,点C与圆的位置关系?
点C在圆外.
点A在圆内,
点B在圆上,
OA < r,
OB = r,
活 动一:问 题 探 究
设⊙O 的半径为r,点P到圆心的距离OP=d,则有:
点P在⊙O内
点P在⊙O上
点P在⊙O外
d<r
d=r
d>r
P
r
d
P
r
d
P
r
d
点与圆的位置关系
O
O
O
P与⊙O位置
d与r数量关系
符号 读作
“等价于”,它表
示从符号的左端可
以得到右端从右端
也可以得到左端.
射击靶图上,有一组以靶心为圆心的大小不同的圆,他们把靶图由内到外分成几个区域,这些区域用由高到底的环数来表示,射击成绩用弹着点位置对应的环数来表示.弹着点与靶心的距离决定了它在哪个圆内,弹着点离靶心越近,它所在的区域就越靠内,对应的环数也就越高,射击的成绩越好.
你知道击中靶上不同位置的成绩是如何计算的吗 ?
1.① 已知⊙O的半径为10厘米,根据下列点P到圆心的距离,判定点P与圆的位置关系,并说明理由.
(1)8厘米;(2)10厘米;(3)12厘米.
2. 已知一点到圆的最小距离为2cm,最大距离为8cm,则该圆的半径为_________.
3cm或5cm
学以致用
②已知⊙O的半径为5cm,点P是⊙O外一点,则 OP的长可能 .
A. 2 B. 3 C. 5 D.7
A/
A
A(3,4)
O
学以致用
3.若⊙A的半径为5,圆心A的坐标为(3,4),点O为坐标原点,则点O的位置为 ( )
A、在⊙A内 B、在⊙A上 C、在⊙A外 D、不能确定
方法点拨:
要判定一个点是否在圆上、圆内、圆外,只需求出此点与圆心的距离,
然后与半径作比较即可.
B
4.如图,已知矩形ABCD的边AB=3,AD=4.
(1)以A为圆心,4为半径作⊙A,则点B、C、D与⊙A的位置关系如何?
解:AD=4=r,故D点在⊙A上
AB=3AC=5>r,故C点在⊙A外
(2)若以A点为圆心作⊙A,使B、C、D三点中至少有一点在圆内,且至少有一点在圆外,求⊙A的半径r的取值范围?(直接写出答案)
3数形结合思想
变式:如图,在直角坐标系中,点A的坐标为(2,1),P是x轴上一点,要使△PAO为等腰三角形,满足条件的P有几个?求出点P的坐标.
(1)如图,做经过已知点A的圆,这样的圆你能做出多少个?
(2)如图做经过已知点A、B的圆,这样的圆你能做出多少个?他们的圆心分布有什么特点?
探究
·
·
·
·
·
·
A
B
A
无数个
无数个,在线段AB的垂直平分线上
A
B
C
1.连结AB,作线段AB的垂直平分线DE,
O
D
E
G
F
2.连结BC,作线段BC的垂直平分线FG,交DE于点O,
3.以O为圆心,OB(OA、OB)为半径作圆,
作法:
⊙O就是所求作的圆
已知:不在同一直线上的三点A、B、C
求作:⊙O,使它经过A、B、C三点。
3.在平面内过不在同一直线上的三点能不能作圆?
类比探究
这样的圆有几个 为什么?
位置关系
有且只有
定理:
不在同一直线上的三个点确定一个圆.
A
B
C
D
E
G
F
●o
归纳总结
圆的内接三角形
三角形的外接圆
三角形的外心
A
B
C
O
外心
1.三边垂直平分线的交点
2.到三个顶点距离相等
三角形的外心是否一定在三角形的内部?
O
A
B
C
A
B
C
O
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
钝角三角形的外心位于三角形外.
规律总结
锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
2. 三角形有且只有一个外接圆 ( )
5. 三角形的外心到三边的距离相等 ( )
3. 任意一个圆有一个内接三角形,并且只有一个内接三角形( )
判断题:
1. 过三点一定可以作圆 ( )
4. 三角形的外心就是这个三角形任意两边垂直平分线的交点( )
抢答环节
【针对训练】
D
3.现在你知道怎样将一个如图所示的破损的圆盘复原了吗?
方法:
1、在圆弧上任取三点A、B、C;
2、作线段AB、BC的垂直平分线,其交点O即为圆心;
3、以点O为圆心,OC长为半径作圆.
⊙O即为所求.
A
B
C
O
经过同一条直线三个点能作出一个圆吗?
思
考
l1
l2
A
B
C
P
如图,假设过同一条直线l上三点A、B、C可以作一个圆,设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,即点P为l1与l2的交点,而l1⊥l,l2⊥l这与我们以前学过的“过一点有且只有一条直线与已知直线垂直”相矛盾,所以过同一条直线上的三点不能作圆.
反证法的定义
要点归纳
先假设命题的结论不成立,然后由此经过推理得出矛盾(常与公理、定理、定义或已知条件相矛盾),由矛盾判定假设不正确,从而得到原命题成立,这种方法叫做反证法.
反证法的一般步骤
假设命题的结论不成立
从这个假设出发,经过推理,得出矛盾
由矛盾判定假设不正确,从而肯定命题的结论正确
例4 求证:在一个三角形中,至少有一个内角小于或等于60°.
已知:△ABC
求证:△ABC中至少有一个内角小于或等于60°.
证明:假设 ,
则 。
∴ ,
即 .
这与 矛盾.假设不成立.
∴ .
△ABC中没有一个内角小于或等于60°
∠A>60°,∠B>60°,∠C>60°
∠A+∠B+∠C=180°
三角形的内角和为180度
△ABC中至少有一个内角小于或等于60°.
∠A+∠B+∠C>60°+60°+60°=180°
点与圆的位置关系
点在圆外
点在圆上
点在圆内
d>r
d=r
d位置关系数量化
作圆
过一点可以作无数个圆
过两点可以作无数个圆
定理:
过不在同一直线上的三个点确定一个圆
一个三角形的外接圆是唯一的.
注意:同一直线上的三个点不能作圆
点P在圆环内
r≤d≤R
R
r
P
课堂小结
锐角三角形:
外心在三角形内部
直角三角形:
外心在斜边中点
钝角三角形:
外心在三角形外部
创设情景 明确目标
我国射击运动员在奥运会上屡获金牌,为祖国赢得荣誉.你知道运动员的成绩是如何计算的吗?
24.2.1 点和圆的位置关系
学习目标
(一)掌握点和圆的三种位置关系。
(二)了解不在同一直线上的三点确定一个圆,以及过不在同一条直线上的三个点作圆的方法;
(三)理解并掌握三角形的外接圆及三角形外心的概念。
我们是如何判断点与圆的位置关系的?
探究一:
r
问题2:设⊙O半径为r,说出来点A,点B,点C与圆心O的距离与半径的关系:
·
C
O
A
B
OC > r.
问题1:观察图中点A,点B,点C与圆的位置关系?
点C在圆外.
点A在圆内,
点B在圆上,
OA < r,
OB = r,
活 动一:问 题 探 究
设⊙O 的半径为r,点P到圆心的距离OP=d,则有:
点P在⊙O内
点P在⊙O上
点P在⊙O外
d<r
d=r
d>r
P
r
d
P
r
d
P
r
d
点与圆的位置关系
O
O
O
P与⊙O位置
d与r数量关系
符号 读作
“等价于”,它表
示从符号的左端可
以得到右端从右端
也可以得到左端.
射击靶图上,有一组以靶心为圆心的大小不同的圆,他们把靶图由内到外分成几个区域,这些区域用由高到底的环数来表示,射击成绩用弹着点位置对应的环数来表示.弹着点与靶心的距离决定了它在哪个圆内,弹着点离靶心越近,它所在的区域就越靠内,对应的环数也就越高,射击的成绩越好.
你知道击中靶上不同位置的成绩是如何计算的吗 ?
1.① 已知⊙O的半径为10厘米,根据下列点P到圆心的距离,判定点P与圆的位置关系,并说明理由.
(1)8厘米;(2)10厘米;(3)12厘米.
2. 已知一点到圆的最小距离为2cm,最大距离为8cm,则该圆的半径为_________.
3cm或5cm
学以致用
②已知⊙O的半径为5cm,点P是⊙O外一点,则 OP的长可能 .
A. 2 B. 3 C. 5 D.7
A/
A
A(3,4)
O
学以致用
3.若⊙A的半径为5,圆心A的坐标为(3,4),点O为坐标原点,则点O的位置为 ( )
A、在⊙A内 B、在⊙A上 C、在⊙A外 D、不能确定
方法点拨:
要判定一个点是否在圆上、圆内、圆外,只需求出此点与圆心的距离,
然后与半径作比较即可.
B
4.如图,已知矩形ABCD的边AB=3,AD=4.
(1)以A为圆心,4为半径作⊙A,则点B、C、D与⊙A的位置关系如何?
解:AD=4=r,故D点在⊙A上
AB=3
(2)若以A点为圆心作⊙A,使B、C、D三点中至少有一点在圆内,且至少有一点在圆外,求⊙A的半径r的取值范围?(直接写出答案)
3
变式:如图,在直角坐标系中,点A的坐标为(2,1),P是x轴上一点,要使△PAO为等腰三角形,满足条件的P有几个?求出点P的坐标.
(1)如图,做经过已知点A的圆,这样的圆你能做出多少个?
(2)如图做经过已知点A、B的圆,这样的圆你能做出多少个?他们的圆心分布有什么特点?
探究
·
·
·
·
·
·
A
B
A
无数个
无数个,在线段AB的垂直平分线上
A
B
C
1.连结AB,作线段AB的垂直平分线DE,
O
D
E
G
F
2.连结BC,作线段BC的垂直平分线FG,交DE于点O,
3.以O为圆心,OB(OA、OB)为半径作圆,
作法:
⊙O就是所求作的圆
已知:不在同一直线上的三点A、B、C
求作:⊙O,使它经过A、B、C三点。
3.在平面内过不在同一直线上的三点能不能作圆?
类比探究
这样的圆有几个 为什么?
位置关系
有且只有
定理:
不在同一直线上的三个点确定一个圆.
A
B
C
D
E
G
F
●o
归纳总结
圆的内接三角形
三角形的外接圆
三角形的外心
A
B
C
O
外心
1.三边垂直平分线的交点
2.到三个顶点距离相等
三角形的外心是否一定在三角形的内部?
O
A
B
C
A
B
C
O
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
钝角三角形的外心位于三角形外.
规律总结
锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
2. 三角形有且只有一个外接圆 ( )
5. 三角形的外心到三边的距离相等 ( )
3. 任意一个圆有一个内接三角形,并且只有一个内接三角形( )
判断题:
1. 过三点一定可以作圆 ( )
4. 三角形的外心就是这个三角形任意两边垂直平分线的交点( )
抢答环节
【针对训练】
D
3.现在你知道怎样将一个如图所示的破损的圆盘复原了吗?
方法:
1、在圆弧上任取三点A、B、C;
2、作线段AB、BC的垂直平分线,其交点O即为圆心;
3、以点O为圆心,OC长为半径作圆.
⊙O即为所求.
A
B
C
O
经过同一条直线三个点能作出一个圆吗?
思
考
l1
l2
A
B
C
P
如图,假设过同一条直线l上三点A、B、C可以作一个圆,设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,即点P为l1与l2的交点,而l1⊥l,l2⊥l这与我们以前学过的“过一点有且只有一条直线与已知直线垂直”相矛盾,所以过同一条直线上的三点不能作圆.
反证法的定义
要点归纳
先假设命题的结论不成立,然后由此经过推理得出矛盾(常与公理、定理、定义或已知条件相矛盾),由矛盾判定假设不正确,从而得到原命题成立,这种方法叫做反证法.
反证法的一般步骤
假设命题的结论不成立
从这个假设出发,经过推理,得出矛盾
由矛盾判定假设不正确,从而肯定命题的结论正确
例4 求证:在一个三角形中,至少有一个内角小于或等于60°.
已知:△ABC
求证:△ABC中至少有一个内角小于或等于60°.
证明:假设 ,
则 。
∴ ,
即 .
这与 矛盾.假设不成立.
∴ .
△ABC中没有一个内角小于或等于60°
∠A>60°,∠B>60°,∠C>60°
∠A+∠B+∠C=180°
三角形的内角和为180度
△ABC中至少有一个内角小于或等于60°.
∠A+∠B+∠C>60°+60°+60°=180°
点与圆的位置关系
点在圆外
点在圆上
点在圆内
d>r
d=r
d
作圆
过一点可以作无数个圆
过两点可以作无数个圆
定理:
过不在同一直线上的三个点确定一个圆
一个三角形的外接圆是唯一的.
注意:同一直线上的三个点不能作圆
点P在圆环内
r≤d≤R
R
r
P
课堂小结
锐角三角形:
外心在三角形内部
直角三角形:
外心在斜边中点
钝角三角形:
外心在三角形外部
同课章节目录
