2022-2023学年七年级上册数学第一章三角形练习(无答案)
文档属性
| 名称 | 2022-2023学年七年级上册数学第一章三角形练习(无答案) | 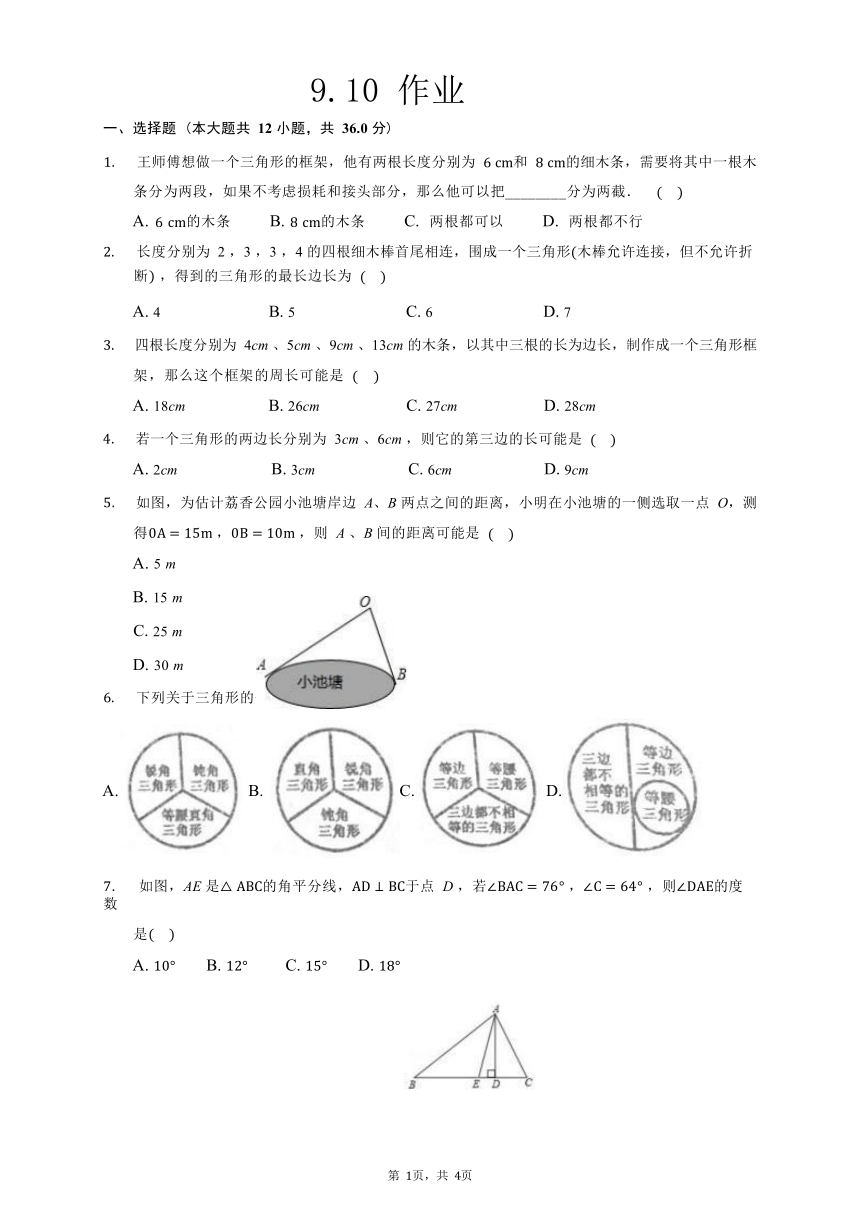 | |
| 格式 | docx | ||
| 文件大小 | 93.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-13 19:30:22 | ||
图片预览

文档简介
9.10 作业
一、选择题 (本大题共 12 小题,共 36.0 分)
1. 王师傅想做一个三角形的框架,他有两根长度分别为 6 cm和 8 cm的细木条,需要将其中一根木
条分为两段,如果不考虑损耗和接头部分,那么他可以把________分为两截. ( )
A. 6 cm的木条 B. 8 cm的木条 C. 两根都可以 D. 两根都不行
2. 长度分别为 2 ,3 ,3 ,4 的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折 断) ,得到的三角形的最长边长为 ( )
A. 4 B. 5 C. 6 D. 7
3. 四根长度分别为 4cm 、5cm 、9cm 、13cm 的木条,以其中三根的长为边长,制作成一个三角形框
架,那么这个框架的周长可能是 ( )
A. 18cm B. 26cm C. 27cm D. 28cm
4. 若一个三角形的两边长分别为 3cm 、6cm ,则它的第三边的长可能是 ( )
A. 2cm B. 3cm C. 6cm D. 9cm
5. 如图,为估计荔香公园小池塘岸边 A、B 两点之间的距离,小明在小池塘的一侧选取一点 O,测
得0A = 15m ,0B = 10m ,则 A 、B 间的距离可能是 ( )
A. 5 m
B. 15 m
C. 25 m
D. 30 m
6. 下列关于三角形的分类,正确的是( )
A.B.C.D.
7. 如图,AE 是△ ABC的角平分线,AD ⊥ BC于点 D ,若∠BAC = 76° ,∠C = 64° ,则∠DAE的度数
是( )
A. 10° B. 12° C. 15° D. 18°
第 1页,共 4页
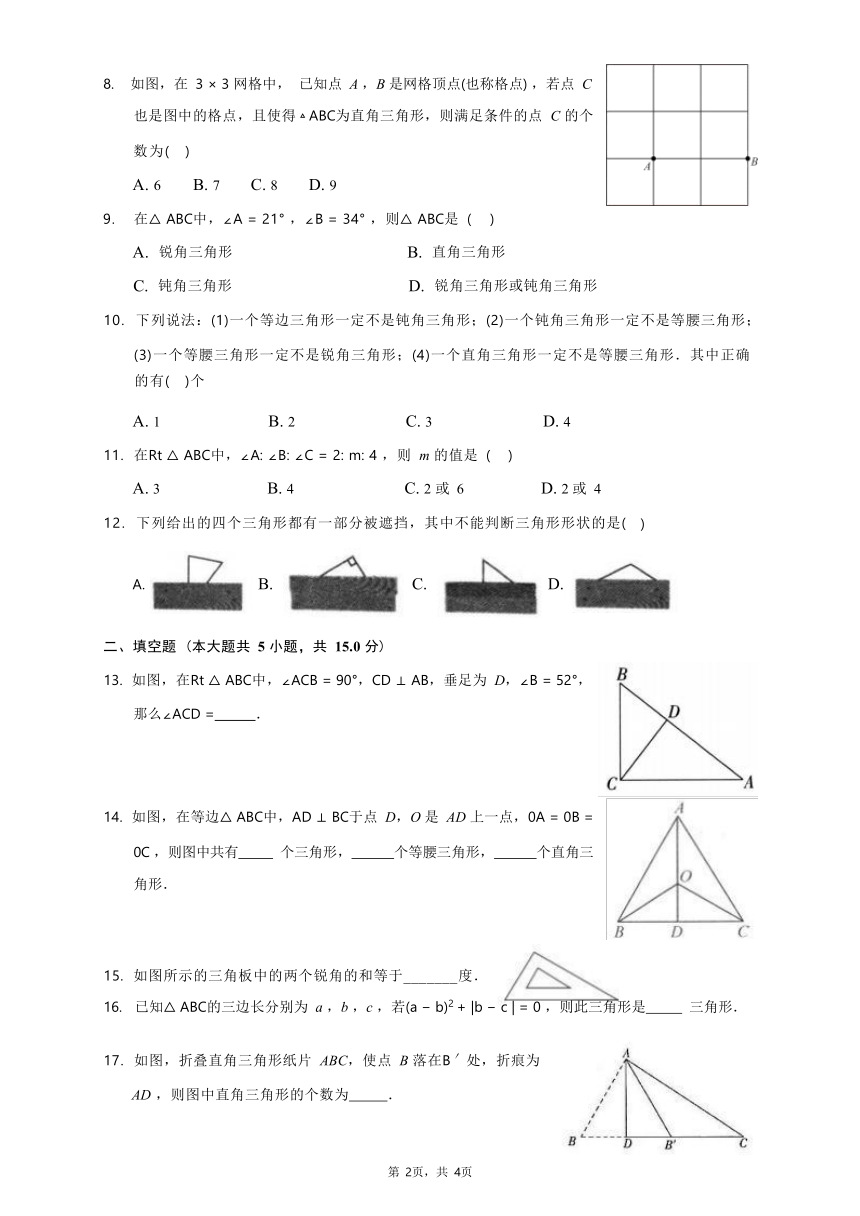
8. 如图,在 3 × 3 网格中, 已知点 A ,B 是网格顶点(也称格点) ,若点 C
也是图中的格点,且使得 ABC为直角三角形,则满足条件的点 C 的个
数为( )
A. 6 B. 7 C. 8 D. 9
9. 在△ ABC中,∠A = 21° ,∠B = 34° ,则△ ABC是 ( )
A. 锐角三角形 B. 直角三角形
C. 钝角三角形 D. 锐角三角形或钝角三角形
10. 下列说法:(1)一个等边三角形一定不是钝角三角形;(2)一个钝角三角形一定不是等腰三角形;
(3)一个等腰三角形一定不是锐角三角形;(4)一个直角三角形一定不是等腰三角形.其中正确 的有( )个
A. 1 B. 2 C. 3 D. 4
11. 在Rt △ ABC中,∠A: ∠B: ∠C = 2: m: 4 ,则 m 的值是 ( )
A. 3 B. 4 C. 2 或 6 D. 2 或 4
12. 下列给出的四个三角形都有一部分被遮挡,其中不能判断三角形形状的是( )
A. B. C. D.
二、填空题 (本大题共 5 小题,共 15.0 分)
13. 如图,在Rt △ ABC中,∠ACB = 90°,CD ⊥ AB,垂足为 D,∠B = 52°,
那么∠ACD = .
14. 如图,在等边△ ABC中,AD ⊥ BC于点 D,O 是 AD 上一点,0A = 0B =
0C ,则图中共有 个三角形, 个等腰三角形, 个直角三
角形.
15. 如图所示的三角板中的两个锐角的和等于_______度.
16. 已知△ ABC的三边长分别为 a ,b ,c ,若(a b)2 + |b c | = 0 ,则此三角形是 三角形.
17. 如图,折叠直角三角形纸片 ABC,使点 B 落在B′处,折痕为
AD ,则图中直角三角形的个数为 .
第 2页,共 4页
三、解答题 (本大题共 5 小题,共 49.0 分)
18. 已知一个等腰三角形的周长是 36 cm ,其中一边长为 8 cm ,求另外两边的长.
19.如图,在△ABC 中,点 D 在 BC 上,∠BAC=70° ,∠2=2∠3 ,∠1=∠C,求∠2 的度数.
20.如图所示,四边形 ABCD 是任意四边形,AC 与 BD 交于点0.求证:AC + BD > (AB + BC + CD + DA).
证明:在△ 0AB中,0A + 0B > AB ,在△ 0AD中,__________,
在△ 0DC中,__________ ,在△__________ 中,__________,
∴ 0A + 0B + 0A + 0D + 0D + 0C + 0B + 0C > AB + BC + CD + DA,
即___________ ,即AC + BD > (AB + BC + CD + DA).
第 3页,共 4页
21.已知△ ABC的三边长分别为 a ,b ,c.
(1)若 a ,b ,c 满足(a b)2 + (b c)2 = 0 ,试判断△ ABC的形状;
(2)若a = 5 ,b = 2 ,且 c 为整数,求△ ABC的周长
22.如图,AD ⊥ BE ,BC ⊥ BE ,∠A = ∠C ,点 C,D ,E 在同一条直线上.
(1)请说明 AB 与 CD 平行.
(2)若∠ABC = 3∠E ,求∠E的度数.
(3)若∠ABC = 120° ,求∠BEC的度数
第 4页,共 4页
一、选择题 (本大题共 12 小题,共 36.0 分)
1. 王师傅想做一个三角形的框架,他有两根长度分别为 6 cm和 8 cm的细木条,需要将其中一根木
条分为两段,如果不考虑损耗和接头部分,那么他可以把________分为两截. ( )
A. 6 cm的木条 B. 8 cm的木条 C. 两根都可以 D. 两根都不行
2. 长度分别为 2 ,3 ,3 ,4 的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折 断) ,得到的三角形的最长边长为 ( )
A. 4 B. 5 C. 6 D. 7
3. 四根长度分别为 4cm 、5cm 、9cm 、13cm 的木条,以其中三根的长为边长,制作成一个三角形框
架,那么这个框架的周长可能是 ( )
A. 18cm B. 26cm C. 27cm D. 28cm
4. 若一个三角形的两边长分别为 3cm 、6cm ,则它的第三边的长可能是 ( )
A. 2cm B. 3cm C. 6cm D. 9cm
5. 如图,为估计荔香公园小池塘岸边 A、B 两点之间的距离,小明在小池塘的一侧选取一点 O,测
得0A = 15m ,0B = 10m ,则 A 、B 间的距离可能是 ( )
A. 5 m
B. 15 m
C. 25 m
D. 30 m
6. 下列关于三角形的分类,正确的是( )
A.B.C.D.
7. 如图,AE 是△ ABC的角平分线,AD ⊥ BC于点 D ,若∠BAC = 76° ,∠C = 64° ,则∠DAE的度数
是( )
A. 10° B. 12° C. 15° D. 18°
第 1页,共 4页
8. 如图,在 3 × 3 网格中, 已知点 A ,B 是网格顶点(也称格点) ,若点 C
也是图中的格点,且使得 ABC为直角三角形,则满足条件的点 C 的个
数为( )
A. 6 B. 7 C. 8 D. 9
9. 在△ ABC中,∠A = 21° ,∠B = 34° ,则△ ABC是 ( )
A. 锐角三角形 B. 直角三角形
C. 钝角三角形 D. 锐角三角形或钝角三角形
10. 下列说法:(1)一个等边三角形一定不是钝角三角形;(2)一个钝角三角形一定不是等腰三角形;
(3)一个等腰三角形一定不是锐角三角形;(4)一个直角三角形一定不是等腰三角形.其中正确 的有( )个
A. 1 B. 2 C. 3 D. 4
11. 在Rt △ ABC中,∠A: ∠B: ∠C = 2: m: 4 ,则 m 的值是 ( )
A. 3 B. 4 C. 2 或 6 D. 2 或 4
12. 下列给出的四个三角形都有一部分被遮挡,其中不能判断三角形形状的是( )
A. B. C. D.
二、填空题 (本大题共 5 小题,共 15.0 分)
13. 如图,在Rt △ ABC中,∠ACB = 90°,CD ⊥ AB,垂足为 D,∠B = 52°,
那么∠ACD = .
14. 如图,在等边△ ABC中,AD ⊥ BC于点 D,O 是 AD 上一点,0A = 0B =
0C ,则图中共有 个三角形, 个等腰三角形, 个直角三
角形.
15. 如图所示的三角板中的两个锐角的和等于_______度.
16. 已知△ ABC的三边长分别为 a ,b ,c ,若(a b)2 + |b c | = 0 ,则此三角形是 三角形.
17. 如图,折叠直角三角形纸片 ABC,使点 B 落在B′处,折痕为
AD ,则图中直角三角形的个数为 .
第 2页,共 4页
三、解答题 (本大题共 5 小题,共 49.0 分)
18. 已知一个等腰三角形的周长是 36 cm ,其中一边长为 8 cm ,求另外两边的长.
19.如图,在△ABC 中,点 D 在 BC 上,∠BAC=70° ,∠2=2∠3 ,∠1=∠C,求∠2 的度数.
20.如图所示,四边形 ABCD 是任意四边形,AC 与 BD 交于点0.求证:AC + BD > (AB + BC + CD + DA).
证明:在△ 0AB中,0A + 0B > AB ,在△ 0AD中,__________,
在△ 0DC中,__________ ,在△__________ 中,__________,
∴ 0A + 0B + 0A + 0D + 0D + 0C + 0B + 0C > AB + BC + CD + DA,
即___________ ,即AC + BD > (AB + BC + CD + DA).
第 3页,共 4页
21.已知△ ABC的三边长分别为 a ,b ,c.
(1)若 a ,b ,c 满足(a b)2 + (b c)2 = 0 ,试判断△ ABC的形状;
(2)若a = 5 ,b = 2 ,且 c 为整数,求△ ABC的周长
22.如图,AD ⊥ BE ,BC ⊥ BE ,∠A = ∠C ,点 C,D ,E 在同一条直线上.
(1)请说明 AB 与 CD 平行.
(2)若∠ABC = 3∠E ,求∠E的度数.
(3)若∠ABC = 120° ,求∠BEC的度数
第 4页,共 4页
