人教A版(2019)必修第一册高中数学4.5-函数的应用(二)精品课件(共40张PPT)
文档属性
| 名称 | 人教A版(2019)必修第一册高中数学4.5-函数的应用(二)精品课件(共40张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 754.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-14 17:27:17 | ||
图片预览











文档简介
(共40张PPT)
4.5函数的应用(二)
必修一第四章
4.5.1函数的零点与方程的解
知识梳理
知识梳理
知识梳理
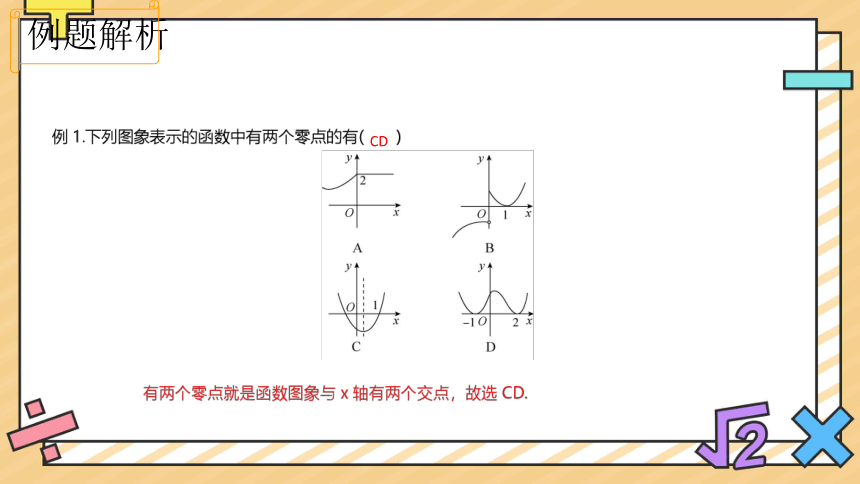
例题解析
例题解析
CD
例题解析
ABD
例题解析
例
3
判断下列函数是否存在零点,如果存在,请求出.
(1)
f
(
x
)
=-
x
2
-
4
x
-
4
;
(2)
f
(
x
)
=
(
x
-
1
)
(
x
2
-
4
x
+
3
)
x
-
3
;
(3)
f
(
x
)
=
4
x
+
5
;
(4)
f
(
x
)
=
log
3
(
x
+
1)
.
例题解析
例4.
函数
f
(
x
)
=
x
-
2
+
log
2
x
,则
f
(
x
)
的零点所在区间为
(
)
A
.
(0,1)
B
.
(1,2)
C
.
(2,3)
D
.
(3,4)
B
例题解析
若函数
f
(
x
)
=
x
+
a
x
(
a
∈
R
)
在区间
(1,2)
上有零点,则
a
的值可能是
(
)
A
.-
2
B
.
0
C
.
1
D
.
3
例5
A
例题解析
例6
.
求函数
f
(
x
)
=
log
2
x
-
x
+
2
的零点的个数.
例题解析
例7.
4.5.2用二分法求方程的近似解
知识梳理
知识梳理
例题解析
B
例题解析
C
例题解析
C
例题解析
例题解析
例题解析
4.5.3函数模型的应用
知识梳理
知识梳理
例题解析
判断正误
(1)
在一次函数模型中,系数
k
的取值会影响函数的性质.
(
)
(2)
在幂函数模型的解析式中,
a
的正负会影响函数的单调性.
(
)
(3)
用函数模型预测的结果和实际结果必须相等,否则函数模型就无存
在意义了.
(
)
例题解析
例1.某公司为激励创新,计划逐年加大研发资金投入.若该公司2020年全年投入研发资金130万元,
在此基础上,每年投入的研发资金比上一年增长12%,则该公司全年投入的研发资金开始超过
200万元的年份是 ( )
(参考数据:lg 1.12≈0.05,lg 1.3≈0.11,lg 2≈0.30)
A.2023年 B.2024年 C.2025年 D.2026年
解:设x年后研发资金开始超过200万元,所以130(1+12%)x>200,
故2024年研发资金开始超过200万元.
B
例题解析
例题解析
例题解析
例
3
.
5G
技术的数学原理之一便是著名的香农公式:
C
=
W
log
2
è
÷
÷
1
+
S
N
.
它表示:在受噪声干扰的信道中,最大信息
传递速率
C
取决于信道带宽
W
、信道内信号的平均功率
S
,
信道内部的高斯噪声功率
N
的大小,其中
S
N
叫做信噪
比
.
按照香农公式,若不改变带宽
W
,而将信噪比
S
N
从
1 000
提升至
2 000
,则
C
大约增加了
A.10%
B.30%
C.50%
D.100%
A
例题解析
例题解析
例题解析
例题解析
例题解析
例题解析
例题解析
例题解析
课堂小结
1.函数零点及零点存在定理;
2.二分法;
3.函数模型。
感谢您的观看
4.5函数的应用(二)
必修一第四章
4.5.1函数的零点与方程的解
知识梳理
知识梳理
知识梳理
例题解析
例题解析
CD
例题解析
ABD
例题解析
例
3
判断下列函数是否存在零点,如果存在,请求出.
(1)
f
(
x
)
=-
x
2
-
4
x
-
4
;
(2)
f
(
x
)
=
(
x
-
1
)
(
x
2
-
4
x
+
3
)
x
-
3
;
(3)
f
(
x
)
=
4
x
+
5
;
(4)
f
(
x
)
=
log
3
(
x
+
1)
.
例题解析
例4.
函数
f
(
x
)
=
x
-
2
+
log
2
x
,则
f
(
x
)
的零点所在区间为
(
)
A
.
(0,1)
B
.
(1,2)
C
.
(2,3)
D
.
(3,4)
B
例题解析
若函数
f
(
x
)
=
x
+
a
x
(
a
∈
R
)
在区间
(1,2)
上有零点,则
a
的值可能是
(
)
A
.-
2
B
.
0
C
.
1
D
.
3
例5
A
例题解析
例6
.
求函数
f
(
x
)
=
log
2
x
-
x
+
2
的零点的个数.
例题解析
例7.
4.5.2用二分法求方程的近似解
知识梳理
知识梳理
例题解析
B
例题解析
C
例题解析
C
例题解析
例题解析
例题解析
4.5.3函数模型的应用
知识梳理
知识梳理
例题解析
判断正误
(1)
在一次函数模型中,系数
k
的取值会影响函数的性质.
(
)
(2)
在幂函数模型的解析式中,
a
的正负会影响函数的单调性.
(
)
(3)
用函数模型预测的结果和实际结果必须相等,否则函数模型就无存
在意义了.
(
)
例题解析
例1.某公司为激励创新,计划逐年加大研发资金投入.若该公司2020年全年投入研发资金130万元,
在此基础上,每年投入的研发资金比上一年增长12%,则该公司全年投入的研发资金开始超过
200万元的年份是 ( )
(参考数据:lg 1.12≈0.05,lg 1.3≈0.11,lg 2≈0.30)
A.2023年 B.2024年 C.2025年 D.2026年
解:设x年后研发资金开始超过200万元,所以130(1+12%)x>200,
故2024年研发资金开始超过200万元.
B
例题解析
例题解析
例题解析
例
3
.
5G
技术的数学原理之一便是著名的香农公式:
C
=
W
log
2
è
÷
÷
1
+
S
N
.
它表示:在受噪声干扰的信道中,最大信息
传递速率
C
取决于信道带宽
W
、信道内信号的平均功率
S
,
信道内部的高斯噪声功率
N
的大小,其中
S
N
叫做信噪
比
.
按照香农公式,若不改变带宽
W
,而将信噪比
S
N
从
1 000
提升至
2 000
,则
C
大约增加了
A.10%
B.30%
C.50%
D.100%
A
例题解析
例题解析
例题解析
例题解析
例题解析
例题解析
例题解析
例题解析
课堂小结
1.函数零点及零点存在定理;
2.二分法;
3.函数模型。
感谢您的观看
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
