27.2.3_相似三角形的周长与面积
文档属性
| 名称 | 27.2.3_相似三角形的周长与面积 |  | |
| 格式 | zip | ||
| 文件大小 | 174.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-11-08 22:17:58 | ||
图片预览






文档简介
课件22张PPT。27.2.3相似三角形的周长与面积
有一只极速乌龟和骄傲的兔子在规定的两块相似四边形的场地上进行比赛,谁先跑完一圈谁为胜,已知:兔子的速度是乌龟的4倍,结果乌龟跑完一圈只用了一个小时,兔子说,我睡上20分钟再跑,也能比你先跑完一圈;你认为兔子的说的话对吗?你能猜到比赛的最后结果吗?故事中的数学相似比2:1(2)相似三角形有什么性质?对应角相等,对应边的比相等(3)相似三角形的对应边的比叫( )
ΔABC与ΔA/B/C/ 的相似 比为k,则
ΔA/B/C/ 与ΔABC的相 似比是( )
相似比(1)相似三角形有哪些判定方法?温故知新学习目标1.理解并掌握相似三角形周长的比等于相似比、面积比等于相似比的平方,并能用来解决简单的问题。
2.探索相似多边形周长的比等于相似比、面积比等于相似比的平方,体验化归思想。
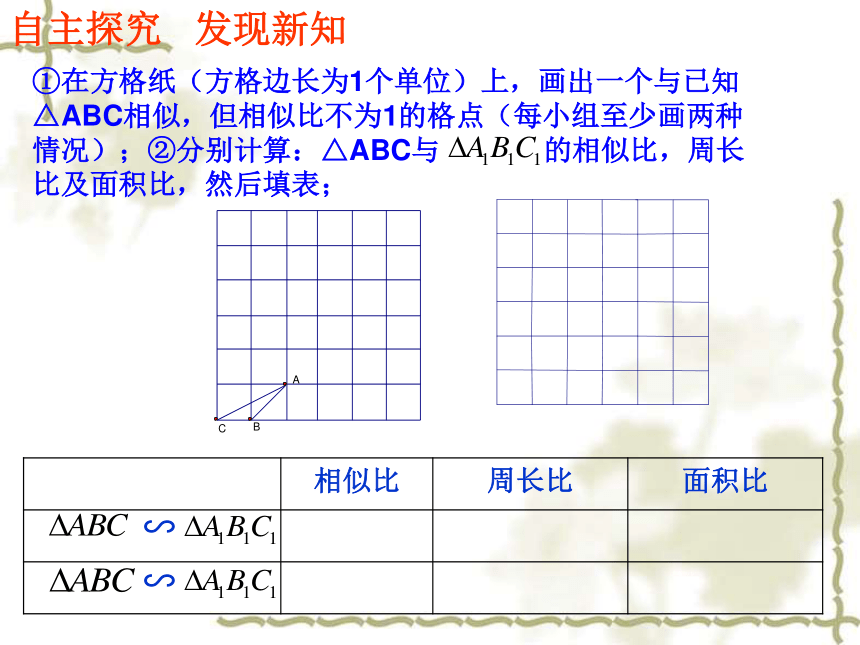
3.在解决实际问题的过程中,增强主动探索、发现数学知识的意识,提高观察、归纳能力和解决问题的能力。①在方格纸(方格边长为1个单位)上,画出一个与已知△ABC相似,但相似比不为1的格点(每小组至少画两种情况);②分别计算:△ABC与 的相似比,周长比及面积比,然后填表;
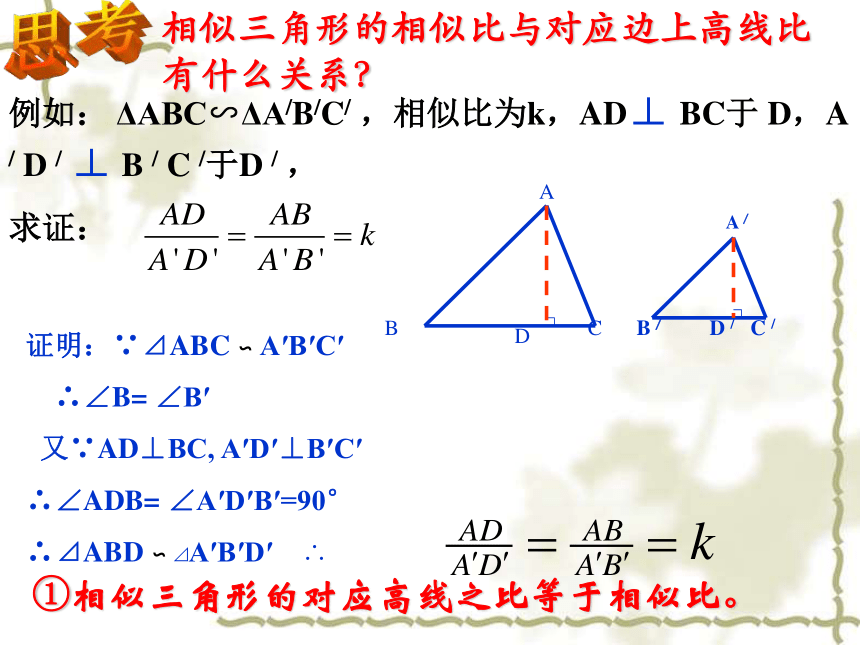
∽自主探究 发现新知∽从以上表中可以看出,当相似比等于k时,周长比等于 ,面积比等于 。由此可以猜想:相似三角形的周长比等于 ,面积比等于 。猜想kk2相似比相似比的平方想一想:对于任何相似三角形,是否也有这样的性质?如果两个三角形相似,它们的周长之间有什么关系?两个相似多边形呢?如果△ABC∽△A'B'C',相似比为k,那么因此AB=k A'B',BC=kB'C',CA=kC'A'从而相似多边形周长的比等于相似比得到:相似三角形周长的比等于相似比探究1想一想三角形中,除了角和边外,还有三种主要线段:高线,角平分线, 中线思考相似三角形的相似比与对应边上高线比有什么关系?例如: ΔABC∽ΔA/B/C/ ,相似比为k,AD⊥ BC于 D,A / D / ⊥ B / C /于D / ,
求证: ①相似三角形的对应高线之比等于相似比。证明:∵⊿ABC ∽ A′B′C′
∴∠B= ∠B′
又∵AD⊥BC, A′D′⊥B′C′
∴∠ADB= ∠A′D′B′=90°
∴⊿ABD ∽ ⊿A′B′D′ ∴
②相似三角形的
对应角平分线之
比,中线之比,
都等于相似比。(1)如图,△ABC∽△A'B'C',相似比为k,它们的面积比是多少?ABCA'B'C'D'D如图,分别作出△ABC和△A'B'C'的高AD和A'D'.∵ ∠ADB =∠A/D/B/ ∠B=∠B'∴ △ABD∽△A'B'D'这样,得到:相似三角形面积的比等于相似比的平方.探究2(2)如图,四边形ABCD相似于四边形A'B'C'D',相似比为k2,它们的面积比是多少?ABCDA'B'C'D'则△ABC∽△A'B'C',△ADC∽△A'C'D',相似多边形面积的比等于相似比的平方.分别连接AC,A'C'例6.如图,在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D,△ABC的周长是24,面积是48,求△DEF的周长和面积.解:在△ABC和△DEF中,∵ AB=2DE,AC=2DF∴又 ∠D=∠A∴ △DEF∽△ABC,相似比为ABCDEF例题赏析 有一只极速乌龟和骄傲的兔子在规定的两块相似四边形的场地上进行比赛,谁先跑完一圈谁为胜,已知:兔子的速度是乌龟的4倍,结果乌龟跑完一圈只用了一个小时,兔子说,我睡上20分钟再跑,也能比你先跑完一圈;你认为兔子的说的话对吗?你能猜到比赛的最后结果吗?你能解决了吗相似比2:1相似三角形的性质对应角相等对应边的比相等对应高的比,对应中线的比、对应角平分线的比都等于相似比.周长的比等于相似比面积的比等于相似比的平方归纳升华在探究过程中你用到了哪些数学思想方法?讨论1.(1)已知ΔABC与ΔA/B/C/ 的相似比为2:3,
则周长比为 ,对应边上中线之比 ,
面积之比为 。
(2)已知ΔABC∽ΔA/B/C/,且面积之比为9:4,
则周长之比为 ,相似比 ,对应边上的
高线之比 。 2:34:93:23: 23:22:3学以致用2.判断
(1)一个三角形的各边长扩大为原来的5倍,这个三角形的周长也扩大为原来的5倍( )
(2)一个四边形的各边长扩大为原来的9倍,这个四边形的面积也扩大为原来的9倍( ).√×3.如图,△ABC∽△A'B'C',他们的周长分别为60cm和72cm,且AB=15cm,B'C'=24cm,求BC、AC、A'B'、A'C'的长.解: ∵△ABC∽△A′B′C′4. 蛋糕店制作两种圆形蛋糕,一种半径是15cm,一种半径是30cm,如果半径是15cm的蛋糕够2个人吃,半径是30cm的蛋糕够多少人吃?(假设两种蛋糕高度相同)解:两块蛋糕是相似的相似比是1:2面积的比为设半径是30cm的蛋糕够x人吃1:4=2:xx = 8答:半径是30cm的蛋糕够8个人吃.生活中的数学6.如图,这是圆桌正上方的灯泡(当成一个点)发出的光线照射桌面形成阴影的示意图,已知桌面的直径为1.2米,桌面距离地面为1米,若灯泡距离地面3米,则地面上阴影部分的面积为多少?5. 在一张复印出来的纸上,一个多边形的一条边由原图中的2cm变成了6cm,这次复印的放缩比例是多少?这个多边形的面积发生了怎样的变化? 如图,△ABC是一块锐角三角形余料,
边BC=120毫米,高AD=80毫米,要把它加
工成正方形零件,使正方形的一边在BC上,
其余两个顶点分别在AB、AC上,这个正方
形零件的边长是多少?NMQPEDCBA解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为x毫米。
∵PN∥BC ∴△APN∽ △ABC
∴拓展提升方程思想如图,矩形FGHN内接于△ABC,FG在BC上,NH分别在AB、AC上,且AD⊥BC于D,交NH于E,AD=8cm,BC=24cm,
(1)设矩形的一边长NF=x,求矩形 FGHN 的面积y与x的关系式。(2)你能求出矩形FGHN
的面积y的最大值吗?变式
ΔABC与ΔA/B/C/ 的相似 比为k,则
ΔA/B/C/ 与ΔABC的相 似比是( )
相似比(1)相似三角形有哪些判定方法?温故知新学习目标1.理解并掌握相似三角形周长的比等于相似比、面积比等于相似比的平方,并能用来解决简单的问题。
2.探索相似多边形周长的比等于相似比、面积比等于相似比的平方,体验化归思想。
3.在解决实际问题的过程中,增强主动探索、发现数学知识的意识,提高观察、归纳能力和解决问题的能力。①在方格纸(方格边长为1个单位)上,画出一个与已知△ABC相似,但相似比不为1的格点(每小组至少画两种情况);②分别计算:△ABC与 的相似比,周长比及面积比,然后填表;
∽自主探究 发现新知∽从以上表中可以看出,当相似比等于k时,周长比等于 ,面积比等于 。由此可以猜想:相似三角形的周长比等于 ,面积比等于 。猜想kk2相似比相似比的平方想一想:对于任何相似三角形,是否也有这样的性质?如果两个三角形相似,它们的周长之间有什么关系?两个相似多边形呢?如果△ABC∽△A'B'C',相似比为k,那么因此AB=k A'B',BC=kB'C',CA=kC'A'从而相似多边形周长的比等于相似比得到:相似三角形周长的比等于相似比探究1想一想三角形中,除了角和边外,还有三种主要线段:高线,角平分线, 中线思考相似三角形的相似比与对应边上高线比有什么关系?例如: ΔABC∽ΔA/B/C/ ,相似比为k,AD⊥ BC于 D,A / D / ⊥ B / C /于D / ,
求证: ①相似三角形的对应高线之比等于相似比。证明:∵⊿ABC ∽ A′B′C′
∴∠B= ∠B′
又∵AD⊥BC, A′D′⊥B′C′
∴∠ADB= ∠A′D′B′=90°
∴⊿ABD ∽ ⊿A′B′D′ ∴
②相似三角形的
对应角平分线之
比,中线之比,
都等于相似比。(1)如图,△ABC∽△A'B'C',相似比为k,它们的面积比是多少?ABCA'B'C'D'D如图,分别作出△ABC和△A'B'C'的高AD和A'D'.∵ ∠ADB =∠A/D/B/ ∠B=∠B'∴ △ABD∽△A'B'D'这样,得到:相似三角形面积的比等于相似比的平方.探究2(2)如图,四边形ABCD相似于四边形A'B'C'D',相似比为k2,它们的面积比是多少?ABCDA'B'C'D'则△ABC∽△A'B'C',△ADC∽△A'C'D',相似多边形面积的比等于相似比的平方.分别连接AC,A'C'例6.如图,在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D,△ABC的周长是24,面积是48,求△DEF的周长和面积.解:在△ABC和△DEF中,∵ AB=2DE,AC=2DF∴又 ∠D=∠A∴ △DEF∽△ABC,相似比为ABCDEF例题赏析 有一只极速乌龟和骄傲的兔子在规定的两块相似四边形的场地上进行比赛,谁先跑完一圈谁为胜,已知:兔子的速度是乌龟的4倍,结果乌龟跑完一圈只用了一个小时,兔子说,我睡上20分钟再跑,也能比你先跑完一圈;你认为兔子的说的话对吗?你能猜到比赛的最后结果吗?你能解决了吗相似比2:1相似三角形的性质对应角相等对应边的比相等对应高的比,对应中线的比、对应角平分线的比都等于相似比.周长的比等于相似比面积的比等于相似比的平方归纳升华在探究过程中你用到了哪些数学思想方法?讨论1.(1)已知ΔABC与ΔA/B/C/ 的相似比为2:3,
则周长比为 ,对应边上中线之比 ,
面积之比为 。
(2)已知ΔABC∽ΔA/B/C/,且面积之比为9:4,
则周长之比为 ,相似比 ,对应边上的
高线之比 。 2:34:93:23: 23:22:3学以致用2.判断
(1)一个三角形的各边长扩大为原来的5倍,这个三角形的周长也扩大为原来的5倍( )
(2)一个四边形的各边长扩大为原来的9倍,这个四边形的面积也扩大为原来的9倍( ).√×3.如图,△ABC∽△A'B'C',他们的周长分别为60cm和72cm,且AB=15cm,B'C'=24cm,求BC、AC、A'B'、A'C'的长.解: ∵△ABC∽△A′B′C′4. 蛋糕店制作两种圆形蛋糕,一种半径是15cm,一种半径是30cm,如果半径是15cm的蛋糕够2个人吃,半径是30cm的蛋糕够多少人吃?(假设两种蛋糕高度相同)解:两块蛋糕是相似的相似比是1:2面积的比为设半径是30cm的蛋糕够x人吃1:4=2:xx = 8答:半径是30cm的蛋糕够8个人吃.生活中的数学6.如图,这是圆桌正上方的灯泡(当成一个点)发出的光线照射桌面形成阴影的示意图,已知桌面的直径为1.2米,桌面距离地面为1米,若灯泡距离地面3米,则地面上阴影部分的面积为多少?5. 在一张复印出来的纸上,一个多边形的一条边由原图中的2cm变成了6cm,这次复印的放缩比例是多少?这个多边形的面积发生了怎样的变化? 如图,△ABC是一块锐角三角形余料,
边BC=120毫米,高AD=80毫米,要把它加
工成正方形零件,使正方形的一边在BC上,
其余两个顶点分别在AB、AC上,这个正方
形零件的边长是多少?NMQPEDCBA解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为x毫米。
∵PN∥BC ∴△APN∽ △ABC
∴拓展提升方程思想如图,矩形FGHN内接于△ABC,FG在BC上,NH分别在AB、AC上,且AD⊥BC于D,交NH于E,AD=8cm,BC=24cm,
(1)设矩形的一边长NF=x,求矩形 FGHN 的面积y与x的关系式。(2)你能求出矩形FGHN
的面积y的最大值吗?变式
