1.2.3 绝对值 课件(共19张PPT)
文档属性
| 名称 | 1.2.3 绝对值 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-17 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
沪科版 七年级上册
1.2 数轴、相反和绝对值
第3课时 绝对值
旧知回顾
1.什么是相反数?什么数的相反数是它本身?
答:在一个数前面加上“-”号,即得这个数的相反数.
2.如何求一个数的相反数?互为相反数在数轴上的位置关系是怎样的?
答:只有符号不同的两个数互为相反数;
0的相反数是它本身.
互为相反数的两数位于原点的两侧,并且到原点的距离相等.
探究新知
绝对值的意义
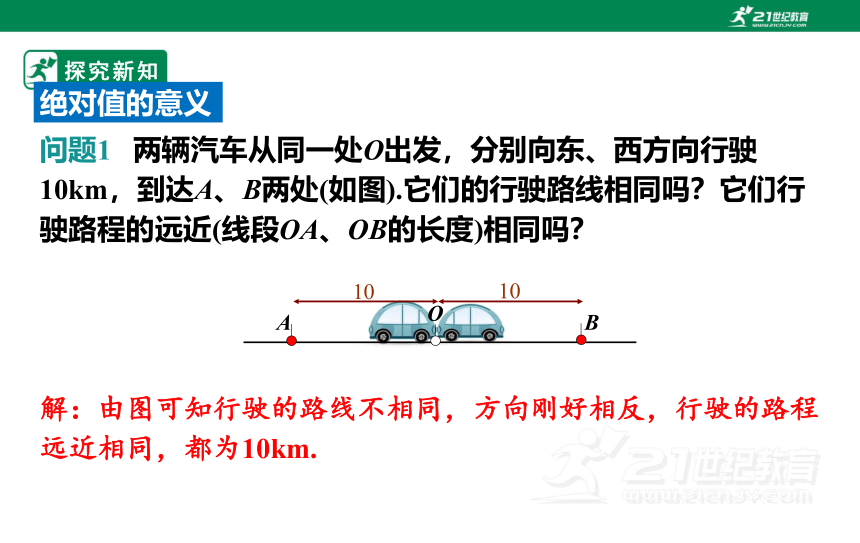
问题1 两辆汽车从同一处O出发,分别向东、西方向行驶10km,到达A、B两处(如图).它们的行驶路线相同吗?它们行驶路程的远近(线段OA、OB的长度)相同吗?
A
O
B
10
10
解:由图可知行驶的路线不相同,方向刚好相反,行驶的路程远近相同,都为10km.
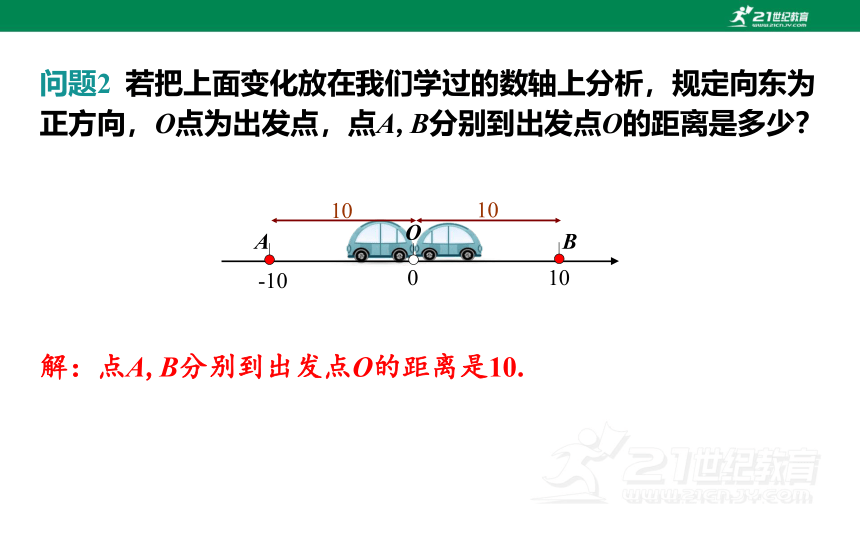
问题2 若把上面变化放在我们学过的数轴上分析,规定向东为正方向,O点为出发点,点A,B分别到出发点O的距离是多少?
A
O
B
10
10
-10
0
10
解:点A,B分别到出发点O的距离是10.
问题3 -10与10是相反数,把它们在数轴上表示出来,它们有什么相同之处和不同之处?
-10与10在数轴上所表示的点到原点的距离都是8个单位长度,它们的符号不同,互为相反数.
-10
10
0
10
10
想一想:互为相反数的两个数到原点的距离都相等吗?
相等
在数轴上,表示数 a 的点到原点的距离,叫做数 a 的绝对值,记作|a|.
这里的数a可以是正数、负数和0.
0
1
2
3
﹣1
﹣2
﹣3
﹣4
﹣5
4
5
|-4|
|4|
例如 +4和-4它们位于原点的两侧,但到原点的距离都等于4,即它们的绝对值都是4,记作|+4|=4,|-4|=4.如图
求下列各数的绝对值:
解:
|﹢1|=1,
|﹣0.1|=0.1,
|4.5|=4.5.
,﹢1,﹣0.1,4.5.
例
1.计算:
|-3.7|= ; -(-3.7)= ;
-|-3.7|= ; -|+3.7|= .
3.7
3.7
-3.7
-3.7
2.(1)①|+8|= , |12|= ;
②|-6|= , |-15|= ;
③|0|= .
8
12
15
6
0
(2)根据(1)中的规律发现:不论正数、负数和零,它们的绝对值一定是_________,即|a|____0.
非负数
≥
典例
1.在数轴上表示-4的点到原点的距离等于( )
A.|4| B.-4
C.±4 D.
A
2.|-10|是数轴上表示________的点到原点的距离.
-10
仿例
1.绝对值是5的数有_____个,是_________;绝对值相等的两个数在数轴上的对应点之间的距离为4,则这两个数分别为__________.
2.一个数的绝对值是它本身,这个数是_________;一个数的绝对值是它的相反数,这个数是_________.
两
5和-5
2和-2
非负数
非正数
变例
绝对值的性质
问题 一个数的绝对值与这个数有什么关系?
例如:|3|=3,|+7|=7 …………
一个正数的绝对值是它本身
例如:|-3|=3,|-2.3|=2.3 …………
一个负数的绝对值是它的相反数
0的绝对值是0,即 |0|=0
而原点到原点的距离是0
由绝对值的定义可知:
即(1)若a > 0,则| a | = a;
(2)若a < 0,则| a | = ﹣a;
(3)若a = 0,则| a | = 0;
a.一个正数的绝对值是它本身;
b.一个负数的绝对值是它的相反数;
c.0的绝对值是0.
1.在有理数中,绝对值等于它本身的数有( )
A.一个 B.两个
C.三个 D.无数个
2.若|a|+|b-2|=0,则a=____,b=____.
D
0
2
典例
3.(1)绝对值是4的数有几个,各是什么?
(2)绝对值是0的数有几个,各是什么?
(3)绝对值是-5的数有几个,各是什么?
典例
解:(1)两个;4和-4;
(2)一个;0;
(3)0个.
1.下列各组数中,互为相反数的是( )
A
仿例
2.(1)若a=-2,b=-3,则|-a|+|b|的值为_____;
(2)若x与2互为相反数,则|x|+2=____.
3.(1)当x=0时,| x |+5取最小值,这个最小值是______;
(2)当a=2时,36-|a-2|取最______值,这个值是______.
5
4
5
36
大
随堂练习
1.填空
|﹣3|=____, |1.5|=____, |0|=____,
|﹣5|=____, |﹣0.02|=______, | |=____,
| |=____, |﹣100|=____.
3
1.5
0
5
0.02
100
2.计算
(1)|﹣8|+|9| (2)|﹣8|÷|﹣8|
(3)|0.6|-| | (4)|﹣3|×|﹣2|
=17
=1
=0
=6
3.下列等式中不成立的是( )
A.|﹣5|= 5 B.﹣|5|= ﹣|﹣5|
C.|﹣5|=|5| D.﹣|﹣5|= 5
D
4.求8,﹣8, , 的绝对值.
|﹣8|=8;
|8|=8;
解:
课堂小结
绝对值
定义
应用
几何意义
代数意义
求一个数的绝对值
用绝对值解决实际问题
由绝对值求数
|a|=a,(a>0)
|a|=-a,(a<0)
|a|=0,(a=0)
在数轴上,表示数a到原点的距离
沪科版 七年级上册
1.2 数轴、相反和绝对值
第3课时 绝对值
旧知回顾
1.什么是相反数?什么数的相反数是它本身?
答:在一个数前面加上“-”号,即得这个数的相反数.
2.如何求一个数的相反数?互为相反数在数轴上的位置关系是怎样的?
答:只有符号不同的两个数互为相反数;
0的相反数是它本身.
互为相反数的两数位于原点的两侧,并且到原点的距离相等.
探究新知
绝对值的意义
问题1 两辆汽车从同一处O出发,分别向东、西方向行驶10km,到达A、B两处(如图).它们的行驶路线相同吗?它们行驶路程的远近(线段OA、OB的长度)相同吗?
A
O
B
10
10
解:由图可知行驶的路线不相同,方向刚好相反,行驶的路程远近相同,都为10km.
问题2 若把上面变化放在我们学过的数轴上分析,规定向东为正方向,O点为出发点,点A,B分别到出发点O的距离是多少?
A
O
B
10
10
-10
0
10
解:点A,B分别到出发点O的距离是10.
问题3 -10与10是相反数,把它们在数轴上表示出来,它们有什么相同之处和不同之处?
-10与10在数轴上所表示的点到原点的距离都是8个单位长度,它们的符号不同,互为相反数.
-10
10
0
10
10
想一想:互为相反数的两个数到原点的距离都相等吗?
相等
在数轴上,表示数 a 的点到原点的距离,叫做数 a 的绝对值,记作|a|.
这里的数a可以是正数、负数和0.
0
1
2
3
﹣1
﹣2
﹣3
﹣4
﹣5
4
5
|-4|
|4|
例如 +4和-4它们位于原点的两侧,但到原点的距离都等于4,即它们的绝对值都是4,记作|+4|=4,|-4|=4.如图
求下列各数的绝对值:
解:
|﹢1|=1,
|﹣0.1|=0.1,
|4.5|=4.5.
,﹢1,﹣0.1,4.5.
例
1.计算:
|-3.7|= ; -(-3.7)= ;
-|-3.7|= ; -|+3.7|= .
3.7
3.7
-3.7
-3.7
2.(1)①|+8|= , |12|= ;
②|-6|= , |-15|= ;
③|0|= .
8
12
15
6
0
(2)根据(1)中的规律发现:不论正数、负数和零,它们的绝对值一定是_________,即|a|____0.
非负数
≥
典例
1.在数轴上表示-4的点到原点的距离等于( )
A.|4| B.-4
C.±4 D.
A
2.|-10|是数轴上表示________的点到原点的距离.
-10
仿例
1.绝对值是5的数有_____个,是_________;绝对值相等的两个数在数轴上的对应点之间的距离为4,则这两个数分别为__________.
2.一个数的绝对值是它本身,这个数是_________;一个数的绝对值是它的相反数,这个数是_________.
两
5和-5
2和-2
非负数
非正数
变例
绝对值的性质
问题 一个数的绝对值与这个数有什么关系?
例如:|3|=3,|+7|=7 …………
一个正数的绝对值是它本身
例如:|-3|=3,|-2.3|=2.3 …………
一个负数的绝对值是它的相反数
0的绝对值是0,即 |0|=0
而原点到原点的距离是0
由绝对值的定义可知:
即(1)若a > 0,则| a | = a;
(2)若a < 0,则| a | = ﹣a;
(3)若a = 0,则| a | = 0;
a.一个正数的绝对值是它本身;
b.一个负数的绝对值是它的相反数;
c.0的绝对值是0.
1.在有理数中,绝对值等于它本身的数有( )
A.一个 B.两个
C.三个 D.无数个
2.若|a|+|b-2|=0,则a=____,b=____.
D
0
2
典例
3.(1)绝对值是4的数有几个,各是什么?
(2)绝对值是0的数有几个,各是什么?
(3)绝对值是-5的数有几个,各是什么?
典例
解:(1)两个;4和-4;
(2)一个;0;
(3)0个.
1.下列各组数中,互为相反数的是( )
A
仿例
2.(1)若a=-2,b=-3,则|-a|+|b|的值为_____;
(2)若x与2互为相反数,则|x|+2=____.
3.(1)当x=0时,| x |+5取最小值,这个最小值是______;
(2)当a=2时,36-|a-2|取最______值,这个值是______.
5
4
5
36
大
随堂练习
1.填空
|﹣3|=____, |1.5|=____, |0|=____,
|﹣5|=____, |﹣0.02|=______, | |=____,
| |=____, |﹣100|=____.
3
1.5
0
5
0.02
100
2.计算
(1)|﹣8|+|9| (2)|﹣8|÷|﹣8|
(3)|0.6|-| | (4)|﹣3|×|﹣2|
=17
=1
=0
=6
3.下列等式中不成立的是( )
A.|﹣5|= 5 B.﹣|5|= ﹣|﹣5|
C.|﹣5|=|5| D.﹣|﹣5|= 5
D
4.求8,﹣8, , 的绝对值.
|﹣8|=8;
|8|=8;
解:
课堂小结
绝对值
定义
应用
几何意义
代数意义
求一个数的绝对值
用绝对值解决实际问题
由绝对值求数
|a|=a,(a>0)
|a|=-a,(a<0)
|a|=0,(a=0)
在数轴上,表示数a到原点的距离
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
