1.4.3 加、减混合运算 课件(共27张PPT)
文档属性
| 名称 | 1.4.3 加、减混合运算 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-17 08:38:47 | ||
图片预览








文档简介
(共27张PPT)
沪科版 七年级上册
1.4 有理数的加减
第3课时 加、减混合运算
旧知回顾
1.有理数的减法法则是什么?
2.加法的交换律、结合律用字母如何表示?
3.计算5+(-13)与(-13)+5,[(-6)+(-12)]+5与-6+[(-12)+5]它们的结果相同吗?
答:减去一个数,等于加上这个数的相反数.
答:a+b=b+a,a+(b+c)=(a+b)+c.
解:相同.
探究新知
加法的运算律
(1)(-30)+20=
(2)20 +(-30)=
(3)8+(-5)=
(4)(-5)+8 =
(5)[8+(-5)]+(-4)=
(6) 8+[(-5)+(-4)]=
-10
-10
3
3
-1
-1
根据上节课学过的内容,完成下面各题:
现在我们来探究引入负数后,加法运算律是否还成立.
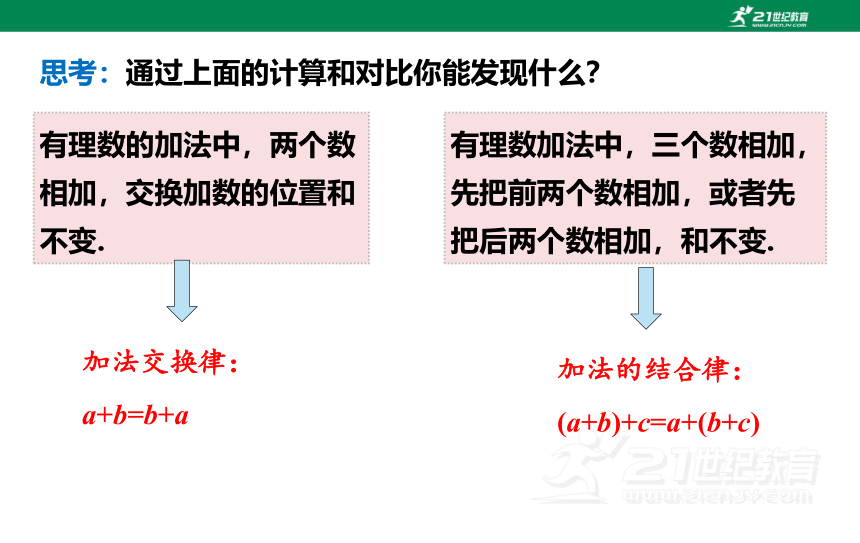
有理数的加法中,两个数相加,交换加数的位置和不变.
加法交换律:
a+b=b+a
有理数加法中,三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
加法的结合律:
(a+b)+c=a+(b+c)
思考:通过上面的计算和对比你能发现什么?
问题 某地冬天某日的气温变化情况如下:早晨6:00的气温为﹣2℃,到中午12:00上升8℃,到14:00又上升了5℃,且为当天的最高气温,到18:00降低了7℃,到23:00又降低了4℃.问:23:00的气温是多少?
用正、负数表示气温的上升与下降,那么问题就转化为求:
(﹣2)+(﹢8)+(﹢5)+(﹣7)+(﹣4) ①
(﹣2)+(﹢8)+(﹢5)+(﹣7)+(﹣4) ①
=(﹣2)+(﹣7)+(﹣4)+(﹢8)+(﹢5) 加法交换律
=[(﹣2)+(﹣7)+(﹣4)]+[(﹢8)+(﹢5)] 加法结合律
=﹣13+13
=0
①式中仅含有加法运算,通常可省去加号及各个括号,写成:﹣2+8+5﹣7﹣4.
典例
运用加法的运算律计算下列各题:
(1) 24+(-15)+7+(-20);
解:原式=(24+7)+[(-15)+(-20)]
例题与练习
=31+(-35)
=-4;
解:
解:
=4+(-4)
=0.
B
仿例
2.下面算式中运用了哪些运算律,填在题后括号内.
(1) (-5)+17+5=(-5)+5+17;( )
( )
加法交换律
加法结合律
3.若a、b互为相反数,则(-2014)+a+2014+b= .
0
仿例
加法交换律和结合律运算方法:
1.互为相反数的两个数先相加;
2.同分母的分数先相加;
3.几个数相加得整数时先相加,即凑整;
4.符号相同的数先相加.
例题与练习
例1
袋 号 1 2 3 4 5 6 7 8 9 10
与标准质量 的差/kg ﹢1 ﹣0.5 ﹣1.5 ﹢0.75 ﹣0.25 ﹢1.5 ﹣1 ﹢0.5 0 ﹢0.5
省略加号和括号的和的形式
如左图,一批大米,标准质量为每袋25kg.质检部门抽取10袋样品进行检测,把超过标准质量的千克数用正数表示,不足的用负数表示,结果如下表:
这10袋大米总计质量是多少千克?
解: 1+(﹣0.5)+(﹣1.5)+0.75+(﹣0.25)+1.5+(﹣1)+0.5+0+0.5
=[1+(﹣1)]+[(﹣0.5)+0.5]+[(﹣1.5)+1.5]+[0.75+(﹣0.25)]+0.5
=1(kg).
25×10+1=251(kg)
答:这10袋大米的总计质量是251kg.
计算:
(1)(﹢7)-(﹢8)+(﹣3)-(﹣6)+2;
解:(1)(﹢7)-(﹢8)+(﹣3)-(﹣6)+2
=(﹢7)+(﹣8)+(﹣3)+(﹢6)+2(减法法则)
=(7+6+2)+(﹣8-3) (加法交换律、结合律)
=15-11
=4
例2
(2)
(2)
解:
有理数加减混合运算的步骤:
(1)将减法转化为加法运算;
(2)省略加号和括号;
(3)运用加法交换律和结合律,将同号两数相加;
(4)按有理数加法法则计算.
将改写成全部是加法运(-8)-(+4)+(-7)-(+9)+(-1)算的式子 ,再把它写成省略加号和括号的和的形式 ,结果读作
或读作 .
(-8)+(-4)+(-7)+(-9)+(-1)
-8-4-7-9-1
负8与负4与负7与负9与负1的和
负8减4减7减9减1
典例
的形式.
仿例
仿例
3.食品店一周中各天的盈亏情况如下(盈余为正):132元,-12.5元,-10.5元,127元,-87元,136.5元,98元.一周总的盈亏情况是( )
A.383.5元 B.578.5元
C.-383.5元 D.-578.5元
A
仿例
4.一个式子可读作“负8与正4与负6与正2 与负3.5的和”,则这个式子的计算结果为 .
-11
5.某冷库的温度是零下10℃,上升-3℃后,又下降5℃,则两次变化后的温度是 ℃.
-18
仿例
随堂练习
1.下列交换加数的位置的变形中,正确的是( )
A.1-4+5-4=1-4+4-5
B.
C.1-2+3-4=2-1+4-3
D.4.5-1.7-2.5+1=4.5-2.5+1-1.7
D
2.计算:(1)23+(-17)+6+(-22);
解:原式=(23+6)+[(-17)+(-22)]
=29-39
=-10
解:原式=(3+1+2)+[(-2)+(-3)+(-4)]
= 6-9
= -3
(2)(-2)+3+1+(-3)+2+(-4);
=-2
3.某公路养护小组乘车沿南北方向巡视维修,某天早晨他们从A地出发,晚上最后到达B地,约定向北为正方向,当天的行驶记录如下(单位:千米):
+18,-9,+7,-14,+13,-6,-8.
(1)B地在A地何方,相距多少千米?
(2)若汽车行驶1千米耗油0.6升,求该天耗油多少升.
(2)(18+9+7+14+13+6+8)×0.6=45(升).
答:该天耗油45升.
解:(1) (+18)+(-9)+(+7)+(-14)+(+13)+(-6)+(-8)
=[(+18)+(+7)+(+13)]+[(-9)+(-14)+(-6)+(-8)]
=38+(-37)
=1(千米).
故B地在A地正北方,相距1千米;
4.红星队在4场足球赛中的战绩是:第一场3∶1胜,第二场2∶3负,第三场0∶0平,第四场2 ∶5负,红星队在4场比赛中总的净胜球数是多少?
解:(+3)+(-1)+(+2)+(-3)+0+0+(+2)+(-5)
=3-1+2-3+2-5
= 3-3+2+2-1-5
= 0+4-6
= -2
答:红星队在4场比赛中总的净胜球数是-2.
课堂小结
加减混合运算
运算律
运算
方法
应用
加法交换律:a+b=b+a
加法结合律:(a+b)+c=a+(b+c)
将加减运算
统一写成加
法的形式
省略加号的和的形式
两种读法
多个有理数的加减
列式计算
计算步骤
沪科版 七年级上册
1.4 有理数的加减
第3课时 加、减混合运算
旧知回顾
1.有理数的减法法则是什么?
2.加法的交换律、结合律用字母如何表示?
3.计算5+(-13)与(-13)+5,[(-6)+(-12)]+5与-6+[(-12)+5]它们的结果相同吗?
答:减去一个数,等于加上这个数的相反数.
答:a+b=b+a,a+(b+c)=(a+b)+c.
解:相同.
探究新知
加法的运算律
(1)(-30)+20=
(2)20 +(-30)=
(3)8+(-5)=
(4)(-5)+8 =
(5)[8+(-5)]+(-4)=
(6) 8+[(-5)+(-4)]=
-10
-10
3
3
-1
-1
根据上节课学过的内容,完成下面各题:
现在我们来探究引入负数后,加法运算律是否还成立.
有理数的加法中,两个数相加,交换加数的位置和不变.
加法交换律:
a+b=b+a
有理数加法中,三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
加法的结合律:
(a+b)+c=a+(b+c)
思考:通过上面的计算和对比你能发现什么?
问题 某地冬天某日的气温变化情况如下:早晨6:00的气温为﹣2℃,到中午12:00上升8℃,到14:00又上升了5℃,且为当天的最高气温,到18:00降低了7℃,到23:00又降低了4℃.问:23:00的气温是多少?
用正、负数表示气温的上升与下降,那么问题就转化为求:
(﹣2)+(﹢8)+(﹢5)+(﹣7)+(﹣4) ①
(﹣2)+(﹢8)+(﹢5)+(﹣7)+(﹣4) ①
=(﹣2)+(﹣7)+(﹣4)+(﹢8)+(﹢5) 加法交换律
=[(﹣2)+(﹣7)+(﹣4)]+[(﹢8)+(﹢5)] 加法结合律
=﹣13+13
=0
①式中仅含有加法运算,通常可省去加号及各个括号,写成:﹣2+8+5﹣7﹣4.
典例
运用加法的运算律计算下列各题:
(1) 24+(-15)+7+(-20);
解:原式=(24+7)+[(-15)+(-20)]
例题与练习
=31+(-35)
=-4;
解:
解:
=4+(-4)
=0.
B
仿例
2.下面算式中运用了哪些运算律,填在题后括号内.
(1) (-5)+17+5=(-5)+5+17;( )
( )
加法交换律
加法结合律
3.若a、b互为相反数,则(-2014)+a+2014+b= .
0
仿例
加法交换律和结合律运算方法:
1.互为相反数的两个数先相加;
2.同分母的分数先相加;
3.几个数相加得整数时先相加,即凑整;
4.符号相同的数先相加.
例题与练习
例1
袋 号 1 2 3 4 5 6 7 8 9 10
与标准质量 的差/kg ﹢1 ﹣0.5 ﹣1.5 ﹢0.75 ﹣0.25 ﹢1.5 ﹣1 ﹢0.5 0 ﹢0.5
省略加号和括号的和的形式
如左图,一批大米,标准质量为每袋25kg.质检部门抽取10袋样品进行检测,把超过标准质量的千克数用正数表示,不足的用负数表示,结果如下表:
这10袋大米总计质量是多少千克?
解: 1+(﹣0.5)+(﹣1.5)+0.75+(﹣0.25)+1.5+(﹣1)+0.5+0+0.5
=[1+(﹣1)]+[(﹣0.5)+0.5]+[(﹣1.5)+1.5]+[0.75+(﹣0.25)]+0.5
=1(kg).
25×10+1=251(kg)
答:这10袋大米的总计质量是251kg.
计算:
(1)(﹢7)-(﹢8)+(﹣3)-(﹣6)+2;
解:(1)(﹢7)-(﹢8)+(﹣3)-(﹣6)+2
=(﹢7)+(﹣8)+(﹣3)+(﹢6)+2(减法法则)
=(7+6+2)+(﹣8-3) (加法交换律、结合律)
=15-11
=4
例2
(2)
(2)
解:
有理数加减混合运算的步骤:
(1)将减法转化为加法运算;
(2)省略加号和括号;
(3)运用加法交换律和结合律,将同号两数相加;
(4)按有理数加法法则计算.
将改写成全部是加法运(-8)-(+4)+(-7)-(+9)+(-1)算的式子 ,再把它写成省略加号和括号的和的形式 ,结果读作
或读作 .
(-8)+(-4)+(-7)+(-9)+(-1)
-8-4-7-9-1
负8与负4与负7与负9与负1的和
负8减4减7减9减1
典例
的形式.
仿例
仿例
3.食品店一周中各天的盈亏情况如下(盈余为正):132元,-12.5元,-10.5元,127元,-87元,136.5元,98元.一周总的盈亏情况是( )
A.383.5元 B.578.5元
C.-383.5元 D.-578.5元
A
仿例
4.一个式子可读作“负8与正4与负6与正2 与负3.5的和”,则这个式子的计算结果为 .
-11
5.某冷库的温度是零下10℃,上升-3℃后,又下降5℃,则两次变化后的温度是 ℃.
-18
仿例
随堂练习
1.下列交换加数的位置的变形中,正确的是( )
A.1-4+5-4=1-4+4-5
B.
C.1-2+3-4=2-1+4-3
D.4.5-1.7-2.5+1=4.5-2.5+1-1.7
D
2.计算:(1)23+(-17)+6+(-22);
解:原式=(23+6)+[(-17)+(-22)]
=29-39
=-10
解:原式=(3+1+2)+[(-2)+(-3)+(-4)]
= 6-9
= -3
(2)(-2)+3+1+(-3)+2+(-4);
=-2
3.某公路养护小组乘车沿南北方向巡视维修,某天早晨他们从A地出发,晚上最后到达B地,约定向北为正方向,当天的行驶记录如下(单位:千米):
+18,-9,+7,-14,+13,-6,-8.
(1)B地在A地何方,相距多少千米?
(2)若汽车行驶1千米耗油0.6升,求该天耗油多少升.
(2)(18+9+7+14+13+6+8)×0.6=45(升).
答:该天耗油45升.
解:(1) (+18)+(-9)+(+7)+(-14)+(+13)+(-6)+(-8)
=[(+18)+(+7)+(+13)]+[(-9)+(-14)+(-6)+(-8)]
=38+(-37)
=1(千米).
故B地在A地正北方,相距1千米;
4.红星队在4场足球赛中的战绩是:第一场3∶1胜,第二场2∶3负,第三场0∶0平,第四场2 ∶5负,红星队在4场比赛中总的净胜球数是多少?
解:(+3)+(-1)+(+2)+(-3)+0+0+(+2)+(-5)
=3-1+2-3+2-5
= 3-3+2+2-1-5
= 0+4-6
= -2
答:红星队在4场比赛中总的净胜球数是-2.
课堂小结
加减混合运算
运算律
运算
方法
应用
加法交换律:a+b=b+a
加法结合律:(a+b)+c=a+(b+c)
将加减运算
统一写成加
法的形式
省略加号的和的形式
两种读法
多个有理数的加减
列式计算
计算步骤
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
