3.2 一元一次方程的应用 课件(共21张PPT)
文档属性
| 名称 | 3.2 一元一次方程的应用 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1003.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-14 13:58:13 | ||
图片预览







文档简介
(共21张PPT)
3.2 一元一次方程的应用
沪科版 七年级上册
导入新课
旧知回顾
1.解一元一次方程的一般步骤有哪些?
答:(1)去分母;
(2)去括号;
(3)移项;
(4)合并同类项;
(5)系数化为1.
2.你能解决下面问题吗?
5位教师和一群学生一起去公园,教师按全票的票价是每人7元,学生只收半价.如果买门票共花费206.50元,那么学生有多少人?
解:设有学生 x人,由题意得:
5×7+ ×7x=206.50,
解得x=49.
答:学生有49人.
探究新知
列一元一次方程解应用题
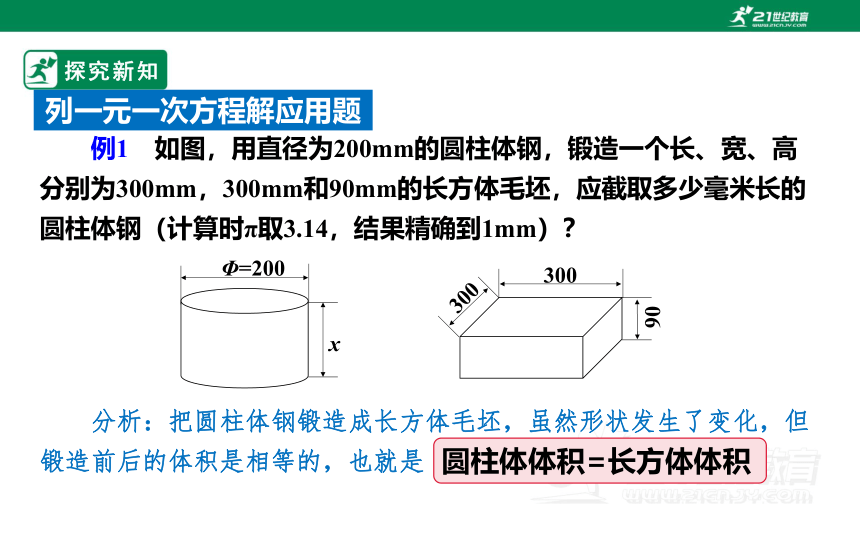
例1 如图,用直径为200mm的圆柱体钢,锻造一个长、宽、高分别为300mm,300mm和90mm的长方体毛坯,应截取多少毫米长的圆柱体钢(计算时π取3.14,结果精确到1mm)?
x
Φ=200
90
300
300
分析:把圆柱体钢锻造成长方体毛坯,虽然形状发生了变化,但锻造前后的体积是相等的,也就是
圆柱体体积=长方体体积
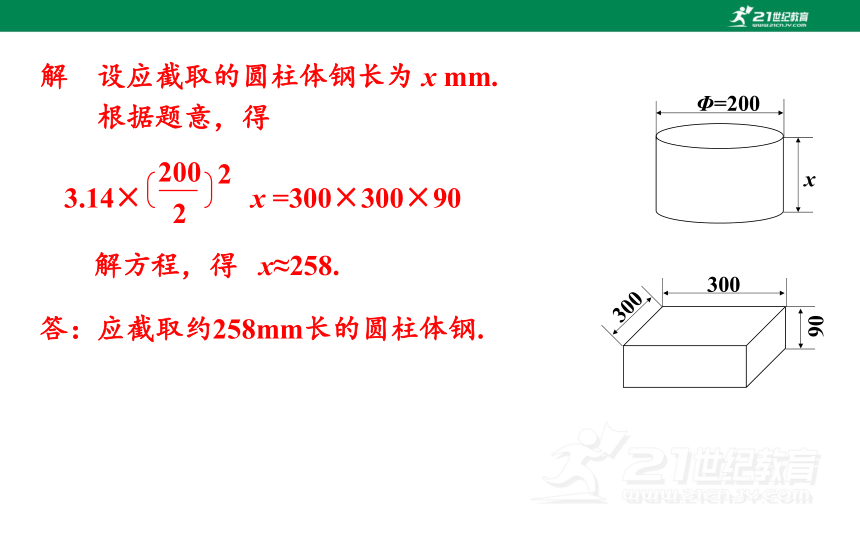
解 设应截取的圆柱体钢长为 x mm.
根据题意,得
3.14× x =300×300×90
200
2
2
解方程,得 x≈258.
答:应截取约258mm长的圆柱体钢.
x
Φ=200
90
300
300
例题与练习
一个圆柱形水桶,底面半径为11 cm,高25 cm,将满桶的水倒入底面长30 cm,宽20 cm的长方体容器,此长方体容器的高至少为多少才不会有水溢出?(π取3.14,结果精确到0.1 cm)
解:设长方体容器的高为x cm,
依题意,有30×20x=25π×112,
解得x= ≈15.8.
答:长方体容器的高至少为15.8 cm.
典例
例2 为了适应经济的发展,铁路运输再次提速.如果客车行驶的平均速度增加40km/h,提速后由合肥到北京1 110 km的路程只需行驶10h.那么提速前,这趟客车平均每时行驶多少千米?
分析:行程问题中常涉及的量有路程、平均速度、时间.他们之间的基本关系是:
路程=平均速度×时间
解 设提速前客车平均每时行驶x km,
根据题意,得
10(x+40)=1 110
解方程,得 x=71
答:提速前客车的平均速度是71km/h.
甲骑摩托车、乙骑自行车同时从相距250千米的两地相向而行,经过5小时相遇.已知甲每小时行驶的路程是乙每小时行驶的路程的3倍少6千米,则乙骑自行车的速度为( )
A.10千米/小时 B.14千米/小时
C.16千米/小时 D.18千米/小时
B
典例
例3 王大伯3年前把手头一笔钱作为3年定期存款存入银行,年利率为5%.到期后得到本息共23 000元,问当年王大伯存入银行多少钱?
分析:本题中涉及的数量关系有
解 设当年王大伯存入银行x元,
根据题意,得 x+3×5%x=23 000.
解方程,得 x=20 000.
答:当年王大伯存入银行20 000元.
本金×利率×年数=利息
本金+利息=本息和
例4 一商店出售书包时,将一种双肩背的书包按进价提高30%作为标价,然后再按标价的9折出售,这样商店每卖出一个这种书包可盈利8.50元.问这种书包每个进价多少?
分析:买卖商品的问题中涉及的数量关系有
解 设每个书包进价为x元,
根据题意,得 0.9×(1+30%)x – x=8.50.
解方程,得 x=50.
答:这种书包每个进价为50元.
实际售价 – 进价=利润
进价:购进商品时的价格(有时也叫成本价).
有关销售的概念
利润率:利润占进价的百分率,即:
利润率=利润÷进价×100%.
售价:在销售商品时的售出价(有时称成交价,卖出价).
标价:在销售时标出的价(有时称原价,定价).
利润:在销售商品的过程中的纯收入,利润=售价–进价.
进价+提价=标价
售价-进价(成本)=利润
打折促销活动中各个量与量之间有怎样的等量关系?
进价×利润率=利润
标价×折扣率=售价
打折或减价
标价
售价
进价
提价
利润、利润率
●售价、进价、利润的关系式:
商品利润=商品售价—商品进价
●进价、利润、利润率的关系:
利润率=
商品进价
商品利润
×100%
●标价、折扣数、商品售价关系 :
商品售价=标价×
折扣数
10
●商品售价、进价、利润率的关系:
商品售价=商品进价×(1+利润率)
打
折
销
售
例5 三个作业队共同使用水泵排涝,如果三个作业队排涝的土地面积之比为4:5:6,而这一次装运水泵和耗用的电力费用共计120元,三个作业队按土地面积比各应负担多少元?
分析:各个作业队应负担费用与排涝的土地面积成正比,且三个作业队各自应负担费用之和等于120元.由于共有土地4+5+6=15份,因而120元可由15份分担.据此,得解法如下.
解 设每份土地排涝分担费用x元,那么三个作业队应负担费用分别为4x元、5x元、6x元.
根据题意,得 4x+5x+6x=120.
解方程,得 x=8.
4x=32,5x=40,6x=48.
答:三个作业队各应负担32元、40元、48元.
一个两位数,十位数字比个位数字的4倍多1,将两个数字调换顺序后所得数比原数小63,则原数为( )
A.92 B.94
C.96 D.98
A
典例
一件工程,甲独做需15天完成,乙独做需12天完成,现先由甲、乙合作3天后,甲有其他任务,剩下工程由乙单独完成,问乙还要几天才能完成全部工程?
解:设乙还需x天完成这项工程,由题意得:
答:乙还需 天才能完成全部工程.
典例
练习
1.长方形的长与宽之比为5:2,它的周长为56cm,求这个长方形的面积.
解 设长方形的长为5x,那么宽为2x.
根据题意,得 2(5x+2x)=56.
解方程,得 x=4.
5x=20,2x=8.
20×8=160(cm2)
答:这个长方形的面积为160cm2.
知识归纳
列方程解应用题有哪些步骤?
弄清题意和题中的数量关系,用字母(如x,y)表示问题里的未知数;
分析题意,找出相等关系(可借助于示意图、表格等);
根据相等关系,列出需要的代数式,并列出方程;
解这个方程,求出未知数的值;
检查所得的值是否正确和符合实际情形,并写出答案(包括单位名称).
1
2
3
4
5
随堂练习
1、一件商品的售价是40元,利润是15元,则进价是_____元。
2、某商品的进价是80元,想获得25%的利润率,应把售价定为______元。
3、某服装店为了清仓,某件成本为90元的衣服亏损了10%,则卖这件衣服亏了___元。
4、一块手表的成本价是x元,亏损率是30﹪,则这块手表的售价应是__________元。
5、某人买进一批水果,以成本价提高40%后出售,卖得280元,则这批水果的进价是____元。
25
100
9
(x-30%x)
200
6.一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天. 如果由这两个工程队从两端同时施工,要多少天可以铺好这条管线?
解:设 x多少天可以铺好这条管线.
依题意得: + =1 ,
解方程,得: x=8.
答:两个工程队从两端同时施工,要8天可以铺好这条管线.
课堂小结
用一元一次方程解决实际问题的基本过程
实际问题
一元一次方程
设未知数,列方程
解方程
一元一次方程的解(x = a)
实际问题的答案
检 验
3.2 一元一次方程的应用
沪科版 七年级上册
导入新课
旧知回顾
1.解一元一次方程的一般步骤有哪些?
答:(1)去分母;
(2)去括号;
(3)移项;
(4)合并同类项;
(5)系数化为1.
2.你能解决下面问题吗?
5位教师和一群学生一起去公园,教师按全票的票价是每人7元,学生只收半价.如果买门票共花费206.50元,那么学生有多少人?
解:设有学生 x人,由题意得:
5×7+ ×7x=206.50,
解得x=49.
答:学生有49人.
探究新知
列一元一次方程解应用题
例1 如图,用直径为200mm的圆柱体钢,锻造一个长、宽、高分别为300mm,300mm和90mm的长方体毛坯,应截取多少毫米长的圆柱体钢(计算时π取3.14,结果精确到1mm)?
x
Φ=200
90
300
300
分析:把圆柱体钢锻造成长方体毛坯,虽然形状发生了变化,但锻造前后的体积是相等的,也就是
圆柱体体积=长方体体积
解 设应截取的圆柱体钢长为 x mm.
根据题意,得
3.14× x =300×300×90
200
2
2
解方程,得 x≈258.
答:应截取约258mm长的圆柱体钢.
x
Φ=200
90
300
300
例题与练习
一个圆柱形水桶,底面半径为11 cm,高25 cm,将满桶的水倒入底面长30 cm,宽20 cm的长方体容器,此长方体容器的高至少为多少才不会有水溢出?(π取3.14,结果精确到0.1 cm)
解:设长方体容器的高为x cm,
依题意,有30×20x=25π×112,
解得x= ≈15.8.
答:长方体容器的高至少为15.8 cm.
典例
例2 为了适应经济的发展,铁路运输再次提速.如果客车行驶的平均速度增加40km/h,提速后由合肥到北京1 110 km的路程只需行驶10h.那么提速前,这趟客车平均每时行驶多少千米?
分析:行程问题中常涉及的量有路程、平均速度、时间.他们之间的基本关系是:
路程=平均速度×时间
解 设提速前客车平均每时行驶x km,
根据题意,得
10(x+40)=1 110
解方程,得 x=71
答:提速前客车的平均速度是71km/h.
甲骑摩托车、乙骑自行车同时从相距250千米的两地相向而行,经过5小时相遇.已知甲每小时行驶的路程是乙每小时行驶的路程的3倍少6千米,则乙骑自行车的速度为( )
A.10千米/小时 B.14千米/小时
C.16千米/小时 D.18千米/小时
B
典例
例3 王大伯3年前把手头一笔钱作为3年定期存款存入银行,年利率为5%.到期后得到本息共23 000元,问当年王大伯存入银行多少钱?
分析:本题中涉及的数量关系有
解 设当年王大伯存入银行x元,
根据题意,得 x+3×5%x=23 000.
解方程,得 x=20 000.
答:当年王大伯存入银行20 000元.
本金×利率×年数=利息
本金+利息=本息和
例4 一商店出售书包时,将一种双肩背的书包按进价提高30%作为标价,然后再按标价的9折出售,这样商店每卖出一个这种书包可盈利8.50元.问这种书包每个进价多少?
分析:买卖商品的问题中涉及的数量关系有
解 设每个书包进价为x元,
根据题意,得 0.9×(1+30%)x – x=8.50.
解方程,得 x=50.
答:这种书包每个进价为50元.
实际售价 – 进价=利润
进价:购进商品时的价格(有时也叫成本价).
有关销售的概念
利润率:利润占进价的百分率,即:
利润率=利润÷进价×100%.
售价:在销售商品时的售出价(有时称成交价,卖出价).
标价:在销售时标出的价(有时称原价,定价).
利润:在销售商品的过程中的纯收入,利润=售价–进价.
进价+提价=标价
售价-进价(成本)=利润
打折促销活动中各个量与量之间有怎样的等量关系?
进价×利润率=利润
标价×折扣率=售价
打折或减价
标价
售价
进价
提价
利润、利润率
●售价、进价、利润的关系式:
商品利润=商品售价—商品进价
●进价、利润、利润率的关系:
利润率=
商品进价
商品利润
×100%
●标价、折扣数、商品售价关系 :
商品售价=标价×
折扣数
10
●商品售价、进价、利润率的关系:
商品售价=商品进价×(1+利润率)
打
折
销
售
例5 三个作业队共同使用水泵排涝,如果三个作业队排涝的土地面积之比为4:5:6,而这一次装运水泵和耗用的电力费用共计120元,三个作业队按土地面积比各应负担多少元?
分析:各个作业队应负担费用与排涝的土地面积成正比,且三个作业队各自应负担费用之和等于120元.由于共有土地4+5+6=15份,因而120元可由15份分担.据此,得解法如下.
解 设每份土地排涝分担费用x元,那么三个作业队应负担费用分别为4x元、5x元、6x元.
根据题意,得 4x+5x+6x=120.
解方程,得 x=8.
4x=32,5x=40,6x=48.
答:三个作业队各应负担32元、40元、48元.
一个两位数,十位数字比个位数字的4倍多1,将两个数字调换顺序后所得数比原数小63,则原数为( )
A.92 B.94
C.96 D.98
A
典例
一件工程,甲独做需15天完成,乙独做需12天完成,现先由甲、乙合作3天后,甲有其他任务,剩下工程由乙单独完成,问乙还要几天才能完成全部工程?
解:设乙还需x天完成这项工程,由题意得:
答:乙还需 天才能完成全部工程.
典例
练习
1.长方形的长与宽之比为5:2,它的周长为56cm,求这个长方形的面积.
解 设长方形的长为5x,那么宽为2x.
根据题意,得 2(5x+2x)=56.
解方程,得 x=4.
5x=20,2x=8.
20×8=160(cm2)
答:这个长方形的面积为160cm2.
知识归纳
列方程解应用题有哪些步骤?
弄清题意和题中的数量关系,用字母(如x,y)表示问题里的未知数;
分析题意,找出相等关系(可借助于示意图、表格等);
根据相等关系,列出需要的代数式,并列出方程;
解这个方程,求出未知数的值;
检查所得的值是否正确和符合实际情形,并写出答案(包括单位名称).
1
2
3
4
5
随堂练习
1、一件商品的售价是40元,利润是15元,则进价是_____元。
2、某商品的进价是80元,想获得25%的利润率,应把售价定为______元。
3、某服装店为了清仓,某件成本为90元的衣服亏损了10%,则卖这件衣服亏了___元。
4、一块手表的成本价是x元,亏损率是30﹪,则这块手表的售价应是__________元。
5、某人买进一批水果,以成本价提高40%后出售,卖得280元,则这批水果的进价是____元。
25
100
9
(x-30%x)
200
6.一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天. 如果由这两个工程队从两端同时施工,要多少天可以铺好这条管线?
解:设 x多少天可以铺好这条管线.
依题意得: + =1 ,
解方程,得: x=8.
答:两个工程队从两端同时施工,要8天可以铺好这条管线.
课堂小结
用一元一次方程解决实际问题的基本过程
实际问题
一元一次方程
设未知数,列方程
解方程
一元一次方程的解(x = a)
实际问题的答案
检 验
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
