4.6 用尺规作线段与角 课件(共20张PPT)
文档属性
| 名称 | 4.6 用尺规作线段与角 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-17 10:15:37 | ||
图片预览





文档简介
(共20张PPT)
4.6 用尺规作线段与角
沪科版 七年级上册
导入新课
答:同角(或等角)的补角相等;同角(或等角)的余角相等.
旧知回顾
1.什么是角的平分线?
2.什么样的两个角互补?什么样的两个角互余?
3.补(余)角的性质是什么?
答:在角的内部、以角的顶点为端点的一条射线把这个角分成两个相等的角,这条射线叫做角的平分线.
答:两个角的和为一个平角,这两个角互为补角,简称互补;
两个角的和为一个直角,这两个角互为余角,简称互余.
在小学,我们已经会用刻度尺、三角尺、量角器和圆规等工具准确地画出线段、直线、射线、角、三角形等各种几何图形.
请大家看看这些图形,它们是由哪些简单图形组成的?你能画出这些图形吗
探究新知
尺规作图
想一想:如果你只有一个圆规和一把没有刻度的直尺,你能画出这些图案吗?
画图形、设计图案,时常要画线段和角.
画一条线段等于已知线段,可以先用刻度尺量出已知线段的长度,再画出等于这个长度的线段.
画一个角等于已知角,可以先用量角器量出已知角的度数,再画出等于这个度数的角.
几何中,通常用没有刻度的直尺和圆规来画图,这种画图的方法叫做尺规作图.
例题与练习
作法 示范
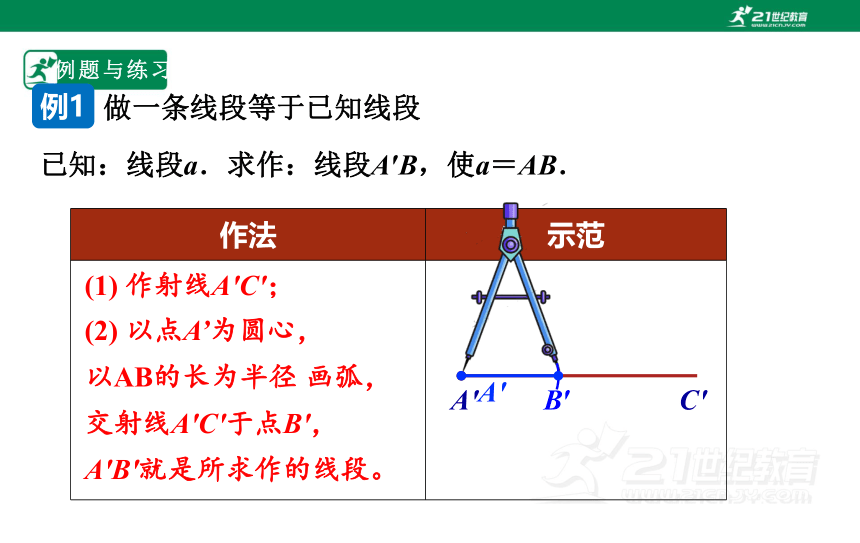
已知:线段a.求作:线段A′B,使a=AB.
做一条线段等于已知线段
例1
(1) 作射线A'C';
A′ C′
(2) 以点A’为圆心,
以AB的长为半径
画弧,
交射线A'C'于点B',
B′
A'B'就是所求作的线段。
A′
A
D
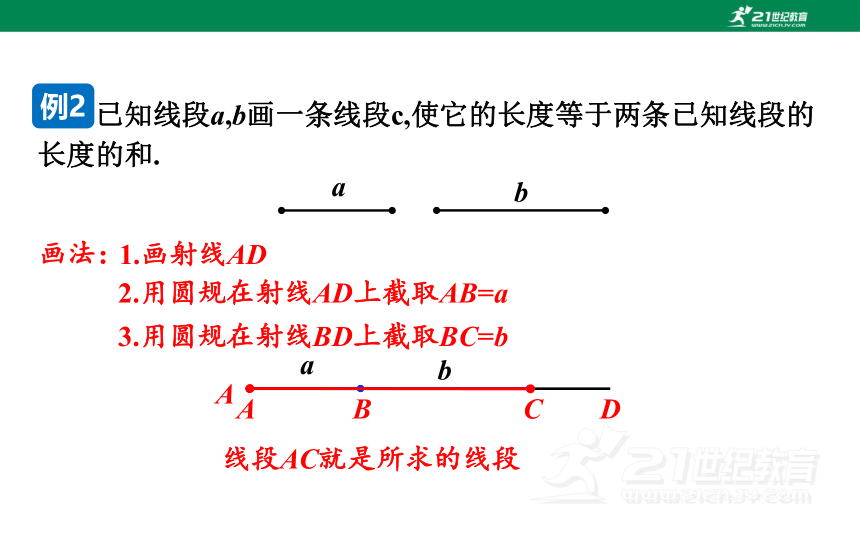
已知线段a,b画一条线段c,使它的长度等于两条已知线段的长度的和.
a
画法:
1.画射线AD
2.用圆规在射线AD上截取AB=a
3.用圆规在射线BD上截取BC=b
线段AC就是所求的线段
例2
b
a
b
B
C
A
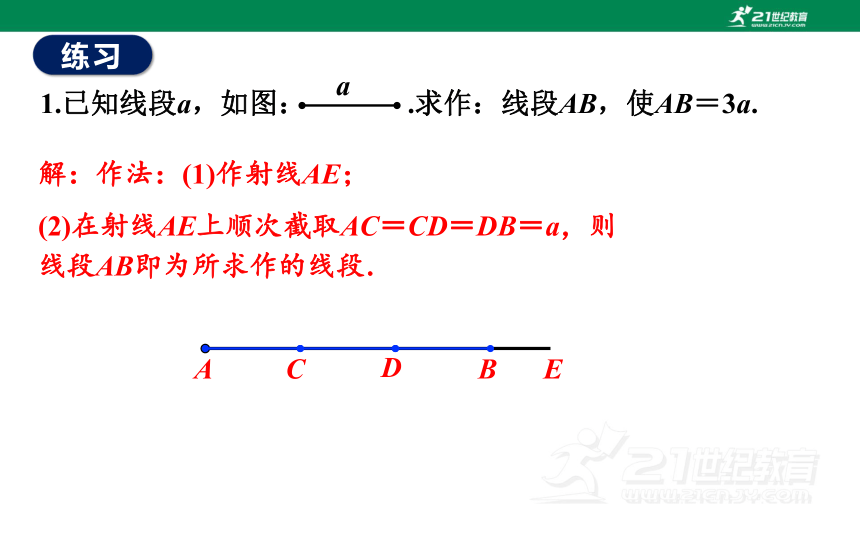
(2)在射线AE上顺次截取AC=CD=DB=a,则线段AB即为所求作的线段.
1.已知线段a,如图: .求作:线段AB,使AB=3a.
a
解:作法:(1)作射线AE;
A
C
D
B
E
练习
探究新知
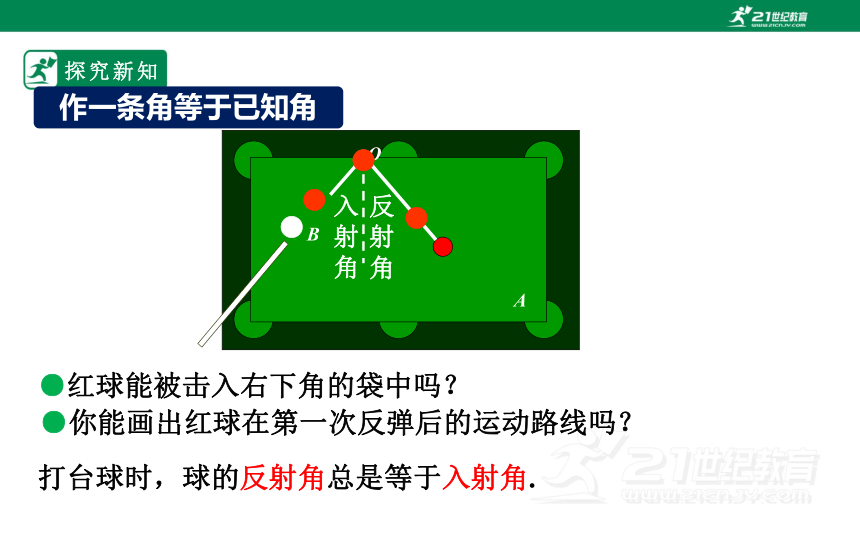
●红球能被击入右下角的袋中吗?
●你能画出红球在第一次反弹后的运动路线吗?
O
B
A
入射角
反射角
打台球时,球的反射角总是等于入射角.
作一条角等于已知角
O
A
想一想:如果入射角是30°,你准备怎样画反射角呢
B
30°
如图∠AOB就是我们所要画的角.
思考:如果入射角不是一个特殊角呢
用三角板画角
●你会利用量角器画一个角等于∠AOB吗?
O
A
B
A
1
O
1
量已知角
画射线
描点
对心,对线,读数
对心,对线
如图∠A1O1B1就是我们所要作的角.
用量角器画角
想一想:如果没有三角尺和量角器,只用尺规作图能画出一个角等于已知角吗?
例2 作一个角等于已知角
已知: 如图,∠AOB.
求作: ∠A'O'B' 使∠A'O'B' =∠AOB.
B
O
A
例3
作法 示范
B
O
A
(2) 以点O为圆心,
任意长为半径
交OA于点C,
(3) 以点O′为圆心,
画弧,
C
D
同样(OC)长为半径
画弧,
C′
(4) 以点C′为圆心,
CD长为半径
画弧,
D′
(5) 过点D′作射线O′B′.
B′
∠A′O′B′就是所求的角.
(1) 作射线O′A′;
交OB 于点D;
交O′A′于点C′;
交前面的弧于点D′,
O′
A′
A′
O′
B′
1.如图,已知∠α和∠β(∠α>∠β),求作∠AOB,使∠AOB=∠α-∠β.
则∠AOB就是所求作的角.
练习
α
β
解:(1)作射线OA;
(2)以射线OA为一边作∠AOC=∠α;
(3)以O为顶点,以射线OC为一边,在∠AOC的内部作∠BOC=∠β,
A
O
C
B
α-β
随堂练习
1.如图,在直线AB上找出一点C,使AC=2CB,
则C点应在( )
D
A.点A、B之间
B.点A的左边
C.点B的右边
D.点A、B之间或点B的右边
A
B
2.如图,已知线段a、b、c,用圆规和直尺画线段,使它等于2a+b-c.
(3)在线段AD上截取DE=c.所以线段AE即为所求.
解:作法:(1)作射线AF;
(2)在射线AF上顺次截取AB=BC=a,CD=b;
A
B
C
E
D
F
2a
b
c
a
b
c
3.已知线段a,b(a>b),画一条线段,使它等于2a-b.
画法:
(1)画射线AE;
(2)在射线AE上顺次截取AB=____=____;
(3)在线段AD上截取____=b,线段_____ 即为所求作的线段
BD
a
CD
AC
A
E
B
C
D
a
a
a
b
b
C′
O′
D′
B′
A′
4.已知:如图,锐角∠AOB,求作:∠β,
使得∠β=180°-2∠AOB.
(3)反向延长射线O′A′到D′,∠β为图中所示的∠C′O′D′.
解:作法:(1)作∠A′O′B′=∠AOB;
(2)以O′B′为始边作∠B′O′C′=∠AOB;
A
O
B
∠β
5.已知: ∠AOB.利用尺规作: ∠A′O′B′ ,使∠A′O′B′=2∠AOB.
B
O
A
作法一:
C
A′
B′
∠A′O′B′为所求.
B
O
A
C
D
C′
E
B′
O′
A
∠A′O′B′为所求.
作法二:
课堂小结
尺规做图的问题,
1.直尺只能用来画线,不能量距.
2.尺规作图要求作出图形,
说明结果,并保留作图痕迹。
4.6 用尺规作线段与角
沪科版 七年级上册
导入新课
答:同角(或等角)的补角相等;同角(或等角)的余角相等.
旧知回顾
1.什么是角的平分线?
2.什么样的两个角互补?什么样的两个角互余?
3.补(余)角的性质是什么?
答:在角的内部、以角的顶点为端点的一条射线把这个角分成两个相等的角,这条射线叫做角的平分线.
答:两个角的和为一个平角,这两个角互为补角,简称互补;
两个角的和为一个直角,这两个角互为余角,简称互余.
在小学,我们已经会用刻度尺、三角尺、量角器和圆规等工具准确地画出线段、直线、射线、角、三角形等各种几何图形.
请大家看看这些图形,它们是由哪些简单图形组成的?你能画出这些图形吗
探究新知
尺规作图
想一想:如果你只有一个圆规和一把没有刻度的直尺,你能画出这些图案吗?
画图形、设计图案,时常要画线段和角.
画一条线段等于已知线段,可以先用刻度尺量出已知线段的长度,再画出等于这个长度的线段.
画一个角等于已知角,可以先用量角器量出已知角的度数,再画出等于这个度数的角.
几何中,通常用没有刻度的直尺和圆规来画图,这种画图的方法叫做尺规作图.
例题与练习
作法 示范
已知:线段a.求作:线段A′B,使a=AB.
做一条线段等于已知线段
例1
(1) 作射线A'C';
A′ C′
(2) 以点A’为圆心,
以AB的长为半径
画弧,
交射线A'C'于点B',
B′
A'B'就是所求作的线段。
A′
A
D
已知线段a,b画一条线段c,使它的长度等于两条已知线段的长度的和.
a
画法:
1.画射线AD
2.用圆规在射线AD上截取AB=a
3.用圆规在射线BD上截取BC=b
线段AC就是所求的线段
例2
b
a
b
B
C
A
(2)在射线AE上顺次截取AC=CD=DB=a,则线段AB即为所求作的线段.
1.已知线段a,如图: .求作:线段AB,使AB=3a.
a
解:作法:(1)作射线AE;
A
C
D
B
E
练习
探究新知
●红球能被击入右下角的袋中吗?
●你能画出红球在第一次反弹后的运动路线吗?
O
B
A
入射角
反射角
打台球时,球的反射角总是等于入射角.
作一条角等于已知角
O
A
想一想:如果入射角是30°,你准备怎样画反射角呢
B
30°
如图∠AOB就是我们所要画的角.
思考:如果入射角不是一个特殊角呢
用三角板画角
●你会利用量角器画一个角等于∠AOB吗?
O
A
B
A
1
O
1
量已知角
画射线
描点
对心,对线,读数
对心,对线
如图∠A1O1B1就是我们所要作的角.
用量角器画角
想一想:如果没有三角尺和量角器,只用尺规作图能画出一个角等于已知角吗?
例2 作一个角等于已知角
已知: 如图,∠AOB.
求作: ∠A'O'B' 使∠A'O'B' =∠AOB.
B
O
A
例3
作法 示范
B
O
A
(2) 以点O为圆心,
任意长为半径
交OA于点C,
(3) 以点O′为圆心,
画弧,
C
D
同样(OC)长为半径
画弧,
C′
(4) 以点C′为圆心,
CD长为半径
画弧,
D′
(5) 过点D′作射线O′B′.
B′
∠A′O′B′就是所求的角.
(1) 作射线O′A′;
交OB 于点D;
交O′A′于点C′;
交前面的弧于点D′,
O′
A′
A′
O′
B′
1.如图,已知∠α和∠β(∠α>∠β),求作∠AOB,使∠AOB=∠α-∠β.
则∠AOB就是所求作的角.
练习
α
β
解:(1)作射线OA;
(2)以射线OA为一边作∠AOC=∠α;
(3)以O为顶点,以射线OC为一边,在∠AOC的内部作∠BOC=∠β,
A
O
C
B
α-β
随堂练习
1.如图,在直线AB上找出一点C,使AC=2CB,
则C点应在( )
D
A.点A、B之间
B.点A的左边
C.点B的右边
D.点A、B之间或点B的右边
A
B
2.如图,已知线段a、b、c,用圆规和直尺画线段,使它等于2a+b-c.
(3)在线段AD上截取DE=c.所以线段AE即为所求.
解:作法:(1)作射线AF;
(2)在射线AF上顺次截取AB=BC=a,CD=b;
A
B
C
E
D
F
2a
b
c
a
b
c
3.已知线段a,b(a>b),画一条线段,使它等于2a-b.
画法:
(1)画射线AE;
(2)在射线AE上顺次截取AB=____=____;
(3)在线段AD上截取____=b,线段_____ 即为所求作的线段
BD
a
CD
AC
A
E
B
C
D
a
a
a
b
b
C′
O′
D′
B′
A′
4.已知:如图,锐角∠AOB,求作:∠β,
使得∠β=180°-2∠AOB.
(3)反向延长射线O′A′到D′,∠β为图中所示的∠C′O′D′.
解:作法:(1)作∠A′O′B′=∠AOB;
(2)以O′B′为始边作∠B′O′C′=∠AOB;
A
O
B
∠β
5.已知: ∠AOB.利用尺规作: ∠A′O′B′ ,使∠A′O′B′=2∠AOB.
B
O
A
作法一:
C
A′
B′
∠A′O′B′为所求.
B
O
A
C
D
C′
E
B′
O′
A
∠A′O′B′为所求.
作法二:
课堂小结
尺规做图的问题,
1.直尺只能用来画线,不能量距.
2.尺规作图要求作出图形,
说明结果,并保留作图痕迹。
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
