《中学教材全解》2013-2014学年九年级数学(下)(河北教育版)第三十五章圆(二)检测题
文档属性
| 名称 | 《中学教材全解》2013-2014学年九年级数学(下)(河北教育版)第三十五章圆(二)检测题 |  | |
| 格式 | zip | ||
| 文件大小 | 249.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-11-07 18:02:39 | ||
图片预览



文档简介
第三十五章 圆(二)检测题
(本检测题满分:120分,时间:100分钟)
一、选择题(每小题3分,共36分)
1.已知⊙O的半径为1,点P到圆心O的距离为R,且方程x2﹣2x+R=0有实数根,则P( )
A. 在⊙O的内部 B. 在⊙O上
C. 在⊙O的外部 D. 在⊙O的内部或圆上
2.(2013 杭州中考)在一个圆中,给出下列命题,其中正确的是( )
A.若圆心到两条直线的距离都等于圆的半径,则这两条直线不可能垂直
B.若圆心到两条直线的距离都小于圆的半径,则这两条直线与圆一定有4个公共点
C.若两条弦所在直线不平行,则这两条弦可能在圆内有公共点
D.若两条弦平行,则这两条弦之间的距离一定小于圆的半径
3.相切两圆的半径分别为,圆心距为d,则d可取的整数值的个数是( )
A. 1 B. 2 C. 3 D. 4
4.已知△ABC面积为18 cm2,BC=12 cm,以A为圆心,BC边上的高为半径的圆与BC( )
A. 相离 B. 相切
C. 相交 D. 位置关系无法确定
5.有一个内角为120°的菱形的内切圆半径为,则该菱形的边长是( )
A. B. C. 4 D. 6
6.如图,AB为⊙O的直径,C、D为⊙O上的点,直线MN切⊙O于C点,图中与∠BCN互余的角有( )
第6题图 第7题图
A. 1个 B. 2个 C. 3个 D. 4个
7.如图,PA、PB分别切⊙O于A、B两点,∠P=40°,则∠C的度数为( )
A. 40° B. 140° C. 70° D. 80°
8.已知OA平分∠BOC,P是OA上一点,以P为圆心的⊙P与OC相切,则⊙P与OB的位置关系为( )
A. 相离 B. 相切 C. 相交 D. 不能确定
9.已知两圆半径分别为R、r(R>r),圆心距为d,且R2+d2﹣r2=2Rd,则两圆的位置关系是( )
A. 内含 B. 外离 C. 内切或外切 D. 相交
10.(2013 长沙中考)已知⊙的半径为1 cm,⊙的半径为3 cm,两圆的圆心距为4 cm,则两圆的位置关系是( )
A.外离 B.外切 C.相交 D.内切
11.(2013 山东青岛中考)直线l与半径为r的⊙O相交,且点O到直线l的距离为6,则r的取值范围是( )
A.r<6 B.r=6 C.r>6 D.r≥6
12.(2013 山东东营中考)已知⊙的半径⊙的半径是方程的根,⊙与⊙的圆心距为1,那么两圆的位置关系为( )
A.内含 B.内切 C.相交 D.外切
二、填空题(每小题3分,共24分)
13. △ABC中,∠C=90°,∠B=60°,AC=3,以C为圆心,r为半径作⊙C,如果点B在圆内,而点A在圆外,那么r的取值范围是 _________ .
14.已知⊙O的半径r=5 cm,圆心O到直线l的距离d=OD=3 cm,在直线l上有P、Q、R 三点,且PD=4 cm,QD>4 cm,RD<4 cm,则P点在⊙O _________ ,Q点在⊙O _________ ,R点在⊙O _________ .
15.在△ABC中,AB=13 cm,BC=12 cm,AC=5 cm,以C为圆心作圆,若要使AB与⊙C相切,则⊙C的半径应为 _________ .
16.两圆半径是方程x2﹣7x+12=0的两根,当圆心距d=1时,两圆的位置关系是 _____ .
17. 如图,△ABC中,∠C=90°,以C为圆心的⊙C与AB相切于点D,若AD=2,BD=4,则⊙C的半径为 _________ .
第17题图 第19题图
18.(2013 贵州六盘水中考)若⊙A和⊙B相切,它们的半径分别为8 cm和2 cm,则圆心距AB为_____cm.
19.(2013 天津中考)如图,PA、PB分别切⊙O于点A、B,若∠P=70°,则∠C的大小 为__________.
20. 两个同心圆的半径分别为3 cm和4 cm,大圆的弦BC与小圆相切,则BC= ________cm.
三、解答题(共60分)
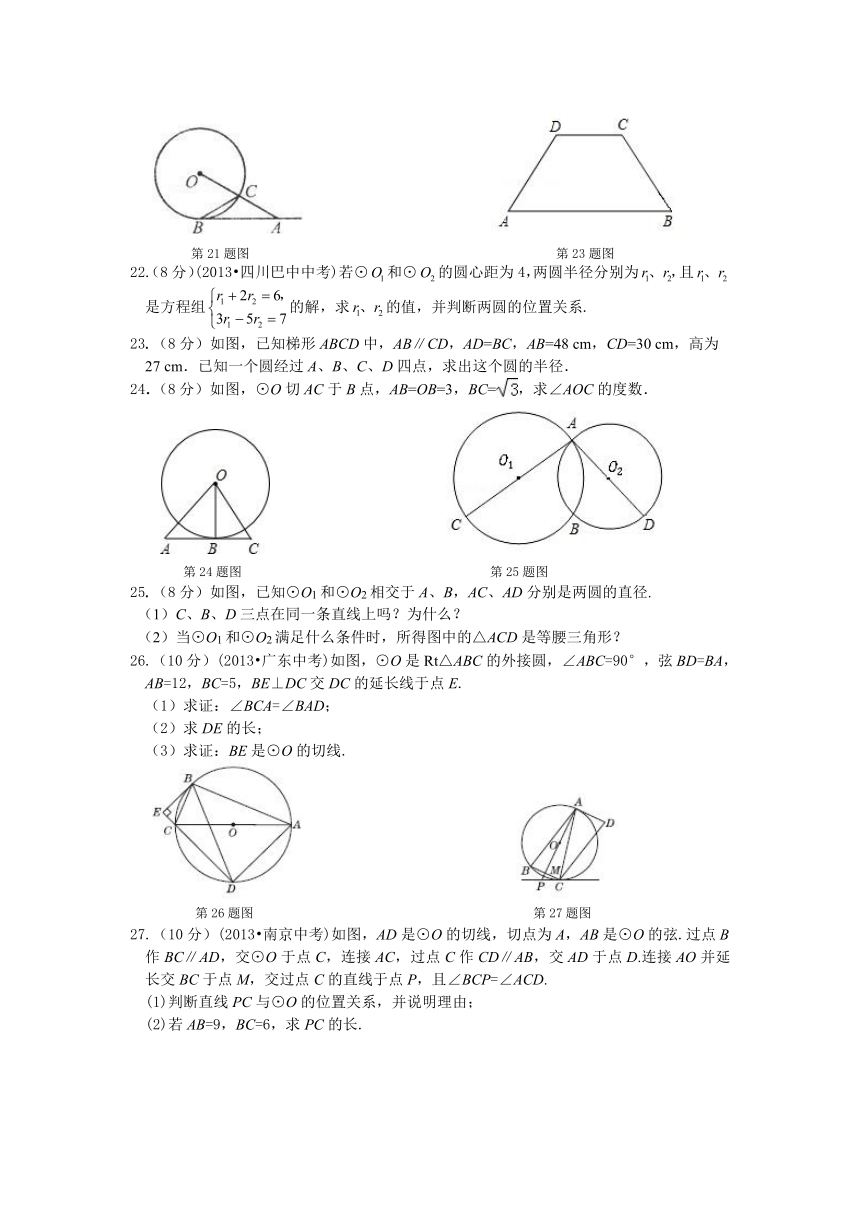
21.(8分)如图,延长⊙O的半径OC到A,使CA=OC,再作弦BC=OC.求证:直线AB是⊙O的切线.
第21题图 第23题图
22.(8分)(2013 四川巴中中考)若⊙和⊙的圆心距为4,两圆半径分别为且是方程组的解,求的值,并判断两圆的位置关系.
23.(8分)如图,已知梯形ABCD中,AB∥CD,AD=BC,AB=48 cm,CD=30 cm,高为27 cm.已知一个圆经过A、B、C、D四点,求出这个圆的半径.
24.(8分)如图,⊙O切AC于B点,AB=OB=3,BC=,求∠AOC的度数.
第24题图 第25题图
25.(8分)如图,已知⊙O1和⊙O2相交于A、B,AC、AD分别是两圆的直径.
(1)C、B、D三点在同一条直线上吗?为什么?
(2)当⊙O1和⊙O2满足什么条件时,所得图中的△ACD是等腰三角形?
26.(10分)(2013 广东中考)如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AB=12,BC=5,BE⊥DC交DC的延长线于点E.
(1)求证:∠BCA=∠BAD;
(2)求DE的长;
(3)求证:BE是⊙O的切线.
第26题图 第27题图
27.(10分)(2013 南京中考)如图,AD是⊙O的切线,切点为A,AB是⊙O的弦.过点B作BC∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D.连接AO并延长交BC于点M,交过点C的直线于点P,且∠BCP=∠ACD.
(1)判断直线PC与⊙O的位置关系,并说明理由;
(2)若AB=9,BC=6,求PC的长.
第三十五章 圆(二)检测题参考答案
1.D 解析:因为方程有实数根,所以Δ=4﹣4R≥0,得R≤1,而圆的半径为1,说明点P到圆心的距离小于或等于半径,所以点P在圆内或圆上.故选D.
2.C 解析:由题意,知A、B、D不正确.
3.A 解析:当两圆外切时,圆心距
当两圆内切时,圆心距
则d可取的整数值是2,只有1个.故选A.
4.B 解析:根据题意画出图形,如图所示.以A为圆心,BC边上的高为半径,则说明BC边上的高等于圆的半径,∴ 该圆与BC相切.故选B.
第4题答图
5.C
6.C 解析:∵ 直线MN切⊙O于C点,∴ ∠BCN=∠BAC,∠ACM=∠D=∠B.
∵ AB为⊙O的直径,∴∠ACB=90°,
∴ ∠BCN+∠ACM=90°,∠B+∠BCN=90°,∠D+∠BCN=90°.故选C.
7.C 解析:如图,连接OA,OB,根据切线的性质定理,切线垂直于过切点的半径,即可求得∠OAP,∠OBP的度数,根据四边形的内角和定理即可求得∠AOB的度数,然后根据圆周角定理即可求解.∵ PA是圆的切线,∴ ∠OAP=90°.同理∠OBP=90°.
根据四边形内角和定理可得:∠AOB=360°﹣∠OAP﹣∠OBP﹣∠P=360°﹣90°﹣90°﹣40°=140°,∴ ∠ACB=∠AOB=70°.故选C.
第7题答图 第8题答图
8.B 解析:如图,连接NP.∵ ⊙P与OC相切,∴ PN⊥OC,即PN为圆的半径.
作PM⊥OB.∵ OA平分∠BOC,由角平分线的性质,得 PM=PN=圆半径.
∴ ⊙P与OB的位置关系为相切.
9.C 解析:∵ R2+d2﹣r2=2Rd,∴(R﹣d)2=r2,解得R﹣d=±r,
∴ ①当R﹣r=d时,两圆内切,
②当R﹣d=﹣r,即R+r=d时,两圆外切.
∴ 两圆的位置关系是内切或外切.故选C.
10.B 解析:因为两圆的圆心距等于两圆半径之和,所以两圆外切.
11.C 解析:设圆心到直线l的距离为d,当d>r时,直线与圆相离;当d=r时,直线与圆相切;当d<r时,直线与圆相交.反之也成立,即直线与圆相交时,r>6,故C项正确.
12.B 解析:解方程,得x=3,经检验,x=3是原方程的根,所以.
因为,两圆的圆心距为1,所以两圆内切.
13.<r<3 解析:∵ △ABC中,∠C=90°,∠B=60°,∴ ∠A=30°,得到AC=BC.又AC=3,得BC=.∵ 点B在圆内,∴ r>BC=.
∵ 点A在圆外,∴ r<AC=3.因此<r<3.
14.上,外,内 解析:如图,OD=3,PD=4,∴ OP==5=r,∴ 点P在圆上.
∵ OD=3,QD>4,∴ OQ=>5,∴ 点Q在圆外.
∵ OD=3,RD<4,∴ OR=<5,∴ 点R在圆内.
15. 解析:如图,设AB与⊙C相切于点D,即CD⊥AB(CD为△ABC斜边AB边上的高,也等于圆C的半径),∵ 132=52+122,即AB2=AC2+BC2(勾股定理),
∴ △ABC为直角三角形.
∵ S△ABC∴CD=,
∴ ⊙C的半径应为.
16.内切 解析:解方程x2﹣7x+12=0,得x1=3,x2=4.
根据题意,得R=4,r=3,d=1,∴ d=R﹣r,∴ 两圆内切.
17.2 解析:如图,连接CD,∵ ⊙C与AB相切于点D,∴ CD⊥AB.
∵ ∠ACD+∠BCD=90°,∠A+∠ACD=90°,∴ ∠A=∠BCD,∴ △ACD∽△CBD,
∴即CD2=AD BD.∵ AD=2,BD=4,∴ CD=2.
第17题答图
18.10或6 解析:本题应分内切和外切两种情况讨论.
∵ ⊙A和⊙B相切,∴ ①当两圆相外切时,圆心距AB=8+2=10(cm);
②当两圆相内切时,圆心距AB=8-2=6(cm).故答案为10或6.
19.55° 解析:分别连接AO、BO,则AO⊥PA,BO⊥PB.
在四边形APBO中,∠P+∠PAO+∠AOB+∠OBP=360°,
∵ ∠P=70°,∠PAO=∠OBP=90°,∴ ∠AOB=110°,
∴ ∠C=∠AOB=55°.
20. 解析:如图,设BC与小圆的切点为D,连接OB、OD.
∵ BC与小圆相切,∴ ∠ODB=90°.
在Rt△OBD中,OB=4 cm,OD=3 cm,
由勾股定理,得
∴ BC=2BD=2 cm.
第20题答图 第21题答图
21.证明:如图,连接OB,
∵ BC=OC,CA=OC,∴ BC为△OBA的中线,且BC=OA,
∴ △OBA为直角三角形,即OB⊥BA.
∴ 直线AB是⊙O的切线.
22.解:∵
①×3-②,得解得把代入①得,∴
∵ ⊙和⊙的圆心距为4,而3<4<5,
∴ 两圆的位置关系为相交.
23.解:如图所示,连接OA、OD,设其外接圆的半径是r,
则r2=OE2+AE2=OF2+DF2.
设OE=x,则OF=27﹣x,即x2+576=(27﹣x)2+225,
解得x=7.可得r=25(cm).
24.解:∵ ⊙O切AC于B点,∴ OB⊥AC.
在Rt△OAB中,AB=OB=3,∴ △OAB为等腰直角三角形,
∴ ∠AOB=45°.
在Rt△OCB中,OB=3,BC=,∴ tan∠BOC=,
∴ ∠BOC=30°,∴ ∠AOC=45°+30°=75°.
25.解:(1)如图①,连接AB、BC、BD,
∵ AC、AD分别是⊙O1和⊙O2的直径,
∴ ∠ABC=90°,∠ABD=90°,∴ ∠CBD=∠ABC+∠ABD=180°.
∴ C、B、D三点在同一条直线上.
(2)如图②,当⊙O1与⊙O2的直径相等,即AC=AD时所得图中的△ACD是等腰三角形;
如图③,当点O2在⊙O1上时,
连接CO2,∵ AC是⊙O1的直径,∴ ∠AO2C=90°,∴ CO2⊥AD.
又O2A=O2D,∴ CA=CD.于是当点O2在⊙O1上时,△ACD是等腰三角形.
如图④,当点O1在⊙O2上时,同理可得DA=DC,所得图中的△ACD是等腰三角形.
第25题答图
26.(1)证明:∵ BA=BD,∴ 弧BA=弧BD.∴ ∠BCA=∠BAD.
(2)解:在Rt△ABC中,
∵ ∠BAC=∠EDB,∠CBA=∠BED=90°,
∴ △ACB∽△DBE,∴
∵ AB=BD=12,∴
(3)证明:如图,连接OB,则OB=OC,
∴ ∠OBC=∠OCB.
∵ ∠ABC=90°,∴ AC是⊙O的直径,∴ ∠ADC=90°.
∴ ∠ABC+∠ADC=180°.
∴ ∠BAD+∠BCD=180°.
又∵ ∠BCE+∠BCD=180°,
∴ ∠BCE=∠BAD.
由(1)知∠BCA=∠BAD,
∴ ∠BCE=∠BCA,即∠BCE=∠BCO,
∴ ∠BCE=∠OBC,∴ OB∥DE.
∵ BE⊥DE,∴ OB⊥BE,∴ BE是⊙O的切线.
27. (1)解法1:直线PC与⊙O相切.
如图(1),连接CO并延长,交⊙O于点N,连接BN.
∵ AB∥CD,∴ ∠BAC=∠ACD.
∵ ∠BAC=∠BNC,∴ ∠BNC=∠ACD.
∵ ∠BCP=∠ACD,∴ ∠BNC=∠BCP.
∵ CN是⊙O的直径,∴ ∠CBN=90°.
∴ ∠BNC+∠BCN=90°,∴ ∠BCP+∠BCN=90°.
∴ ∠PCO=90°,即PC⊥OC.
又∵ 点C在⊙O上,∴ 直线PC与⊙O相切.
(1) (2)
第27题答图
解法2:直线PC与⊙O相切.
如图(2),连接OC.
∵ AD是⊙O的切线,∴ AD⊥OA,即∠OAD=90°.
∵ BC∥AD,∴ ∠OMC=180°-∠OAD=90°,即OM⊥BC.
∴ MC=MB.∴ AB=AC.
∴ ∠MAB=∠MAC,∠BAC=2∠MAC.
又∵ ∠MOC=2∠MAC,∴ ∠MOC=∠BAC.
∵ AB∥CD,∴ ∠BAC=∠ACD.∴ ∠MOC=∠ACD.
又∵ ∠BCP=∠ACD,∴ ∠MOC=∠BCP.
∵ ∠MOC+∠OCM=90°,∴ ∠BCP+∠OCM=90°.
∴ ∠PCO=90°,即PC⊥OC.
又∵ 点C在⊙O上,∴ 直线PC与⊙O相切.
(2)解:∵ AD是⊙O的切线,∴ AD⊥OA,即∠OAD=90°.
∵ BC∥AD,∴ ∠OMC=180°-∠OAD=90°,即OM⊥BC.
∴ MC=MB.∴ AB=AC.
在Rt△AMC中,∠AMC=90°,AC=AB=9,MC=BC=3,
由勾股定理,得
设⊙O的半径为r.
在Rt△OMC中,∠OMC=90°,OM=AM-AO= -r,MC=3,OC=r,
由勾股定理,得 即解得
在△OMC和△OCP中,
∵ ∠OMC=∠OCP,∠MOC=∠COP,∴ △OMC∽△OCP.
∴ 即∴
第14题答图 第15题答图
第第23题答图
第26题答图
(本检测题满分:120分,时间:100分钟)
一、选择题(每小题3分,共36分)
1.已知⊙O的半径为1,点P到圆心O的距离为R,且方程x2﹣2x+R=0有实数根,则P( )
A. 在⊙O的内部 B. 在⊙O上
C. 在⊙O的外部 D. 在⊙O的内部或圆上
2.(2013 杭州中考)在一个圆中,给出下列命题,其中正确的是( )
A.若圆心到两条直线的距离都等于圆的半径,则这两条直线不可能垂直
B.若圆心到两条直线的距离都小于圆的半径,则这两条直线与圆一定有4个公共点
C.若两条弦所在直线不平行,则这两条弦可能在圆内有公共点
D.若两条弦平行,则这两条弦之间的距离一定小于圆的半径
3.相切两圆的半径分别为,圆心距为d,则d可取的整数值的个数是( )
A. 1 B. 2 C. 3 D. 4
4.已知△ABC面积为18 cm2,BC=12 cm,以A为圆心,BC边上的高为半径的圆与BC( )
A. 相离 B. 相切
C. 相交 D. 位置关系无法确定
5.有一个内角为120°的菱形的内切圆半径为,则该菱形的边长是( )
A. B. C. 4 D. 6
6.如图,AB为⊙O的直径,C、D为⊙O上的点,直线MN切⊙O于C点,图中与∠BCN互余的角有( )
第6题图 第7题图
A. 1个 B. 2个 C. 3个 D. 4个
7.如图,PA、PB分别切⊙O于A、B两点,∠P=40°,则∠C的度数为( )
A. 40° B. 140° C. 70° D. 80°
8.已知OA平分∠BOC,P是OA上一点,以P为圆心的⊙P与OC相切,则⊙P与OB的位置关系为( )
A. 相离 B. 相切 C. 相交 D. 不能确定
9.已知两圆半径分别为R、r(R>r),圆心距为d,且R2+d2﹣r2=2Rd,则两圆的位置关系是( )
A. 内含 B. 外离 C. 内切或外切 D. 相交
10.(2013 长沙中考)已知⊙的半径为1 cm,⊙的半径为3 cm,两圆的圆心距为4 cm,则两圆的位置关系是( )
A.外离 B.外切 C.相交 D.内切
11.(2013 山东青岛中考)直线l与半径为r的⊙O相交,且点O到直线l的距离为6,则r的取值范围是( )
A.r<6 B.r=6 C.r>6 D.r≥6
12.(2013 山东东营中考)已知⊙的半径⊙的半径是方程的根,⊙与⊙的圆心距为1,那么两圆的位置关系为( )
A.内含 B.内切 C.相交 D.外切
二、填空题(每小题3分,共24分)
13. △ABC中,∠C=90°,∠B=60°,AC=3,以C为圆心,r为半径作⊙C,如果点B在圆内,而点A在圆外,那么r的取值范围是 _________ .
14.已知⊙O的半径r=5 cm,圆心O到直线l的距离d=OD=3 cm,在直线l上有P、Q、R 三点,且PD=4 cm,QD>4 cm,RD<4 cm,则P点在⊙O _________ ,Q点在⊙O _________ ,R点在⊙O _________ .
15.在△ABC中,AB=13 cm,BC=12 cm,AC=5 cm,以C为圆心作圆,若要使AB与⊙C相切,则⊙C的半径应为 _________ .
16.两圆半径是方程x2﹣7x+12=0的两根,当圆心距d=1时,两圆的位置关系是 _____ .
17. 如图,△ABC中,∠C=90°,以C为圆心的⊙C与AB相切于点D,若AD=2,BD=4,则⊙C的半径为 _________ .
第17题图 第19题图
18.(2013 贵州六盘水中考)若⊙A和⊙B相切,它们的半径分别为8 cm和2 cm,则圆心距AB为_____cm.
19.(2013 天津中考)如图,PA、PB分别切⊙O于点A、B,若∠P=70°,则∠C的大小 为__________.
20. 两个同心圆的半径分别为3 cm和4 cm,大圆的弦BC与小圆相切,则BC= ________cm.
三、解答题(共60分)
21.(8分)如图,延长⊙O的半径OC到A,使CA=OC,再作弦BC=OC.求证:直线AB是⊙O的切线.
第21题图 第23题图
22.(8分)(2013 四川巴中中考)若⊙和⊙的圆心距为4,两圆半径分别为且是方程组的解,求的值,并判断两圆的位置关系.
23.(8分)如图,已知梯形ABCD中,AB∥CD,AD=BC,AB=48 cm,CD=30 cm,高为27 cm.已知一个圆经过A、B、C、D四点,求出这个圆的半径.
24.(8分)如图,⊙O切AC于B点,AB=OB=3,BC=,求∠AOC的度数.
第24题图 第25题图
25.(8分)如图,已知⊙O1和⊙O2相交于A、B,AC、AD分别是两圆的直径.
(1)C、B、D三点在同一条直线上吗?为什么?
(2)当⊙O1和⊙O2满足什么条件时,所得图中的△ACD是等腰三角形?
26.(10分)(2013 广东中考)如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AB=12,BC=5,BE⊥DC交DC的延长线于点E.
(1)求证:∠BCA=∠BAD;
(2)求DE的长;
(3)求证:BE是⊙O的切线.
第26题图 第27题图
27.(10分)(2013 南京中考)如图,AD是⊙O的切线,切点为A,AB是⊙O的弦.过点B作BC∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D.连接AO并延长交BC于点M,交过点C的直线于点P,且∠BCP=∠ACD.
(1)判断直线PC与⊙O的位置关系,并说明理由;
(2)若AB=9,BC=6,求PC的长.
第三十五章 圆(二)检测题参考答案
1.D 解析:因为方程有实数根,所以Δ=4﹣4R≥0,得R≤1,而圆的半径为1,说明点P到圆心的距离小于或等于半径,所以点P在圆内或圆上.故选D.
2.C 解析:由题意,知A、B、D不正确.
3.A 解析:当两圆外切时,圆心距
当两圆内切时,圆心距
则d可取的整数值是2,只有1个.故选A.
4.B 解析:根据题意画出图形,如图所示.以A为圆心,BC边上的高为半径,则说明BC边上的高等于圆的半径,∴ 该圆与BC相切.故选B.
第4题答图
5.C
6.C 解析:∵ 直线MN切⊙O于C点,∴ ∠BCN=∠BAC,∠ACM=∠D=∠B.
∵ AB为⊙O的直径,∴∠ACB=90°,
∴ ∠BCN+∠ACM=90°,∠B+∠BCN=90°,∠D+∠BCN=90°.故选C.
7.C 解析:如图,连接OA,OB,根据切线的性质定理,切线垂直于过切点的半径,即可求得∠OAP,∠OBP的度数,根据四边形的内角和定理即可求得∠AOB的度数,然后根据圆周角定理即可求解.∵ PA是圆的切线,∴ ∠OAP=90°.同理∠OBP=90°.
根据四边形内角和定理可得:∠AOB=360°﹣∠OAP﹣∠OBP﹣∠P=360°﹣90°﹣90°﹣40°=140°,∴ ∠ACB=∠AOB=70°.故选C.
第7题答图 第8题答图
8.B 解析:如图,连接NP.∵ ⊙P与OC相切,∴ PN⊥OC,即PN为圆的半径.
作PM⊥OB.∵ OA平分∠BOC,由角平分线的性质,得 PM=PN=圆半径.
∴ ⊙P与OB的位置关系为相切.
9.C 解析:∵ R2+d2﹣r2=2Rd,∴(R﹣d)2=r2,解得R﹣d=±r,
∴ ①当R﹣r=d时,两圆内切,
②当R﹣d=﹣r,即R+r=d时,两圆外切.
∴ 两圆的位置关系是内切或外切.故选C.
10.B 解析:因为两圆的圆心距等于两圆半径之和,所以两圆外切.
11.C 解析:设圆心到直线l的距离为d,当d>r时,直线与圆相离;当d=r时,直线与圆相切;当d<r时,直线与圆相交.反之也成立,即直线与圆相交时,r>6,故C项正确.
12.B 解析:解方程,得x=3,经检验,x=3是原方程的根,所以.
因为,两圆的圆心距为1,所以两圆内切.
13.<r<3 解析:∵ △ABC中,∠C=90°,∠B=60°,∴ ∠A=30°,得到AC=BC.又AC=3,得BC=.∵ 点B在圆内,∴ r>BC=.
∵ 点A在圆外,∴ r<AC=3.因此<r<3.
14.上,外,内 解析:如图,OD=3,PD=4,∴ OP==5=r,∴ 点P在圆上.
∵ OD=3,QD>4,∴ OQ=>5,∴ 点Q在圆外.
∵ OD=3,RD<4,∴ OR=<5,∴ 点R在圆内.
15. 解析:如图,设AB与⊙C相切于点D,即CD⊥AB(CD为△ABC斜边AB边上的高,也等于圆C的半径),∵ 132=52+122,即AB2=AC2+BC2(勾股定理),
∴ △ABC为直角三角形.
∵ S△ABC∴CD=,
∴ ⊙C的半径应为.
16.内切 解析:解方程x2﹣7x+12=0,得x1=3,x2=4.
根据题意,得R=4,r=3,d=1,∴ d=R﹣r,∴ 两圆内切.
17.2 解析:如图,连接CD,∵ ⊙C与AB相切于点D,∴ CD⊥AB.
∵ ∠ACD+∠BCD=90°,∠A+∠ACD=90°,∴ ∠A=∠BCD,∴ △ACD∽△CBD,
∴即CD2=AD BD.∵ AD=2,BD=4,∴ CD=2.
第17题答图
18.10或6 解析:本题应分内切和外切两种情况讨论.
∵ ⊙A和⊙B相切,∴ ①当两圆相外切时,圆心距AB=8+2=10(cm);
②当两圆相内切时,圆心距AB=8-2=6(cm).故答案为10或6.
19.55° 解析:分别连接AO、BO,则AO⊥PA,BO⊥PB.
在四边形APBO中,∠P+∠PAO+∠AOB+∠OBP=360°,
∵ ∠P=70°,∠PAO=∠OBP=90°,∴ ∠AOB=110°,
∴ ∠C=∠AOB=55°.
20. 解析:如图,设BC与小圆的切点为D,连接OB、OD.
∵ BC与小圆相切,∴ ∠ODB=90°.
在Rt△OBD中,OB=4 cm,OD=3 cm,
由勾股定理,得
∴ BC=2BD=2 cm.
第20题答图 第21题答图
21.证明:如图,连接OB,
∵ BC=OC,CA=OC,∴ BC为△OBA的中线,且BC=OA,
∴ △OBA为直角三角形,即OB⊥BA.
∴ 直线AB是⊙O的切线.
22.解:∵
①×3-②,得解得把代入①得,∴
∵ ⊙和⊙的圆心距为4,而3<4<5,
∴ 两圆的位置关系为相交.
23.解:如图所示,连接OA、OD,设其外接圆的半径是r,
则r2=OE2+AE2=OF2+DF2.
设OE=x,则OF=27﹣x,即x2+576=(27﹣x)2+225,
解得x=7.可得r=25(cm).
24.解:∵ ⊙O切AC于B点,∴ OB⊥AC.
在Rt△OAB中,AB=OB=3,∴ △OAB为等腰直角三角形,
∴ ∠AOB=45°.
在Rt△OCB中,OB=3,BC=,∴ tan∠BOC=,
∴ ∠BOC=30°,∴ ∠AOC=45°+30°=75°.
25.解:(1)如图①,连接AB、BC、BD,
∵ AC、AD分别是⊙O1和⊙O2的直径,
∴ ∠ABC=90°,∠ABD=90°,∴ ∠CBD=∠ABC+∠ABD=180°.
∴ C、B、D三点在同一条直线上.
(2)如图②,当⊙O1与⊙O2的直径相等,即AC=AD时所得图中的△ACD是等腰三角形;
如图③,当点O2在⊙O1上时,
连接CO2,∵ AC是⊙O1的直径,∴ ∠AO2C=90°,∴ CO2⊥AD.
又O2A=O2D,∴ CA=CD.于是当点O2在⊙O1上时,△ACD是等腰三角形.
如图④,当点O1在⊙O2上时,同理可得DA=DC,所得图中的△ACD是等腰三角形.
第25题答图
26.(1)证明:∵ BA=BD,∴ 弧BA=弧BD.∴ ∠BCA=∠BAD.
(2)解:在Rt△ABC中,
∵ ∠BAC=∠EDB,∠CBA=∠BED=90°,
∴ △ACB∽△DBE,∴
∵ AB=BD=12,∴
(3)证明:如图,连接OB,则OB=OC,
∴ ∠OBC=∠OCB.
∵ ∠ABC=90°,∴ AC是⊙O的直径,∴ ∠ADC=90°.
∴ ∠ABC+∠ADC=180°.
∴ ∠BAD+∠BCD=180°.
又∵ ∠BCE+∠BCD=180°,
∴ ∠BCE=∠BAD.
由(1)知∠BCA=∠BAD,
∴ ∠BCE=∠BCA,即∠BCE=∠BCO,
∴ ∠BCE=∠OBC,∴ OB∥DE.
∵ BE⊥DE,∴ OB⊥BE,∴ BE是⊙O的切线.
27. (1)解法1:直线PC与⊙O相切.
如图(1),连接CO并延长,交⊙O于点N,连接BN.
∵ AB∥CD,∴ ∠BAC=∠ACD.
∵ ∠BAC=∠BNC,∴ ∠BNC=∠ACD.
∵ ∠BCP=∠ACD,∴ ∠BNC=∠BCP.
∵ CN是⊙O的直径,∴ ∠CBN=90°.
∴ ∠BNC+∠BCN=90°,∴ ∠BCP+∠BCN=90°.
∴ ∠PCO=90°,即PC⊥OC.
又∵ 点C在⊙O上,∴ 直线PC与⊙O相切.
(1) (2)
第27题答图
解法2:直线PC与⊙O相切.
如图(2),连接OC.
∵ AD是⊙O的切线,∴ AD⊥OA,即∠OAD=90°.
∵ BC∥AD,∴ ∠OMC=180°-∠OAD=90°,即OM⊥BC.
∴ MC=MB.∴ AB=AC.
∴ ∠MAB=∠MAC,∠BAC=2∠MAC.
又∵ ∠MOC=2∠MAC,∴ ∠MOC=∠BAC.
∵ AB∥CD,∴ ∠BAC=∠ACD.∴ ∠MOC=∠ACD.
又∵ ∠BCP=∠ACD,∴ ∠MOC=∠BCP.
∵ ∠MOC+∠OCM=90°,∴ ∠BCP+∠OCM=90°.
∴ ∠PCO=90°,即PC⊥OC.
又∵ 点C在⊙O上,∴ 直线PC与⊙O相切.
(2)解:∵ AD是⊙O的切线,∴ AD⊥OA,即∠OAD=90°.
∵ BC∥AD,∴ ∠OMC=180°-∠OAD=90°,即OM⊥BC.
∴ MC=MB.∴ AB=AC.
在Rt△AMC中,∠AMC=90°,AC=AB=9,MC=BC=3,
由勾股定理,得
设⊙O的半径为r.
在Rt△OMC中,∠OMC=90°,OM=AM-AO= -r,MC=3,OC=r,
由勾股定理,得 即解得
在△OMC和△OCP中,
∵ ∠OMC=∠OCP,∠MOC=∠COP,∴ △OMC∽△OCP.
∴ 即∴
第14题答图 第15题答图
第第23题答图
第26题答图
