《中学教材全解》2013-2014学年九年级数学(下)(江苏科技版)第七章锐角三角函数检测题(含答案)
文档属性
| 名称 | 《中学教材全解》2013-2014学年九年级数学(下)(江苏科技版)第七章锐角三角函数检测题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 138.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-11-07 18:03:26 | ||
图片预览

文档简介
第七章 锐角三角函数检测题
【本检测题满分:100分,时间90分钟】
一、选择题(每小题3分,共30分)
1.在直角三角形中,各边都扩大2倍,则锐角A的正弦值与余弦值都( )
A.缩小2倍 B.扩大2倍 C.不变 D.不能确定
2.在Rt△ABC中,∠C=,BC=4,sin A=,则AC=( )
A.3 B.4 C.5 D.6
3.若∠A是锐角,且sin A=,则( )
A.<∠A< B.<∠A< C.<∠A< D.<∠A<
4.若cos A=,则=( )
A. B. C. D.0
5.在△ABC中,∠A︰∠B︰∠C=1︰1︰2,则=( )
A.1︰1︰2 B. 1︰1︰ C. 1︰1︰ D. 1︰1︰
6.在Rt△ABC中,∠C=,则下列式子成立的是( )
A.sin A=sin B B.sin A=cos B
C.tan A=tan B D.cos A=tan B
7.如图,一个小球由地面沿着坡度的坡面向上前进了10 m,此时小球距离地面的高度为( )
A. B.2 m C.4 m D.m
8.点(-sin 60°,cos 60°)关于y轴对称的点的坐标是( )
A.(,) B.(,) C.(,) D.(,)
9.每周一学校都要举行庄严的升国旗仪式,让我们感受到了国旗的神圣.某同学站在离旗杆12米远的地方,当国旗升起到旗杆顶时,他测得视线的仰角为30°,若这位同学的目高为1.6米,则旗杆的高度约为( )
A.6.9米 B.8.5米 C.10.3米 D.12.0米
10.王英同学从A地沿北偏西60°方向走100 m到B地,再从B地向正南方向走200 m到C地,此时王英同学离A地 ( )
A.50 m B.100 m C.150 m D.100 m
二、填空题(每小题3分,共24分)
11.在Rt△ABC中,∠C=90°,AB=5,AC=3,则sin B=_____.
12.在△ABC中,若BC=,AB=,AC=3,则cos A=________.
13.如图所示,如果△APB绕点B按逆时针方向旋转30°后得到△A'P'B,且BP=2,那么点P与点P'间的长度为___________. (不取近似值. 以下数据供解题使用:sin 15°=,cos 15°=)
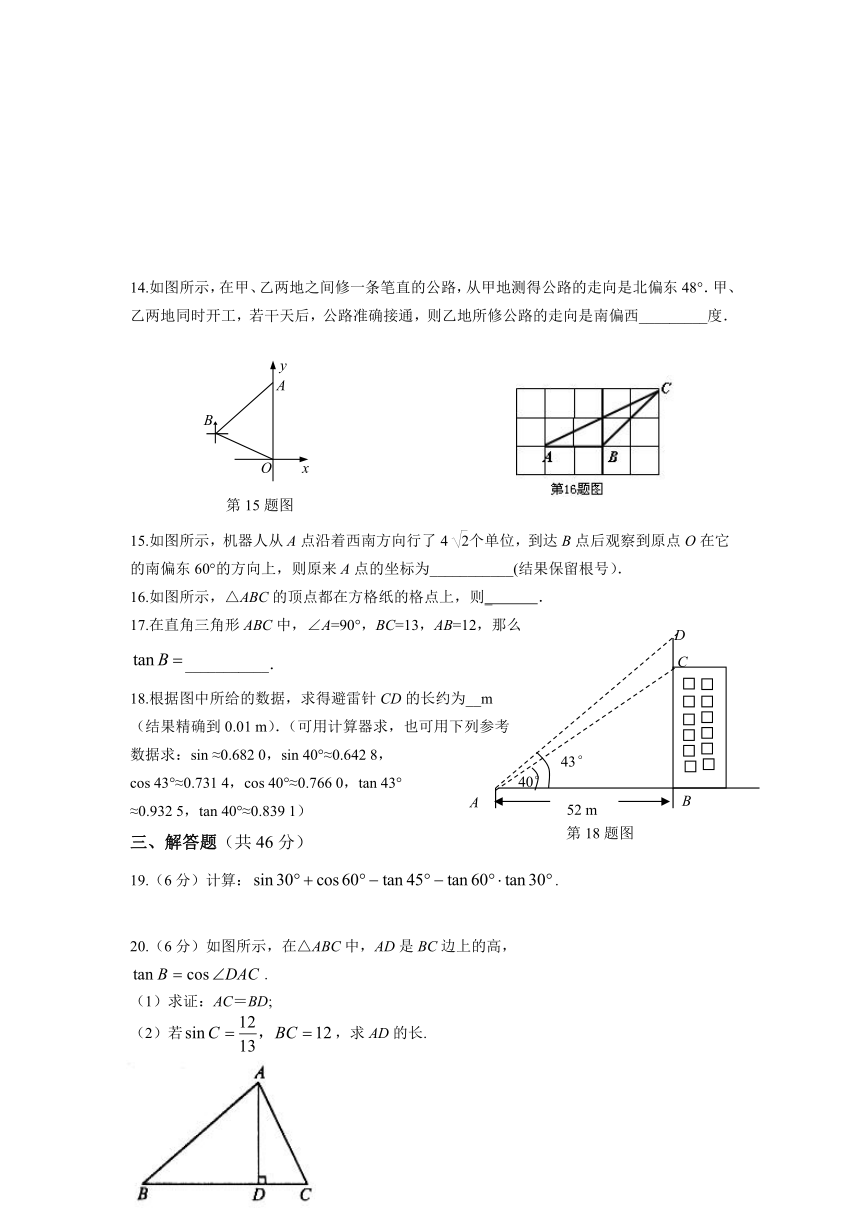
14.如图所示,在甲、乙两地之间修一条笔直的公路,从甲地测得公路的走向是北偏东48°.甲、乙两地同时开工,若干天后,公路准确接通,则乙地所修公路的走向是南偏西_________度.
15.如图所示,机器人从A点沿着西南方向行了4个单位,到达B点后观察到原点O在它的南偏东60°的方向上,则原来A点的坐标为___________(结果保留根号).
16.如图所示,△ABC的顶点都在方格纸的格点上,则_ .
17.在直角三角形ABC中,∠A=90°,BC=13,AB=12,那么
___________.
18.根据图中所给的数据,求得避雷针CD的长约为__m
(结果精确到0.01 m).(可用计算器求,也可用下列参考
数据求:sin ≈0.682 0,sin 40°≈0.642 8,
cos 43°≈0.731 4,cos 40°≈0.766 0,tan 43°
≈0.932 5,tan 40°≈0.839 1)
三、解答题(共46分)
19.(6分)计算:.
20.(6分)如图所示,在△ABC中,AD是BC边上的高,
.
(1)求证:AC=BD;
(2)若,求AD的长.
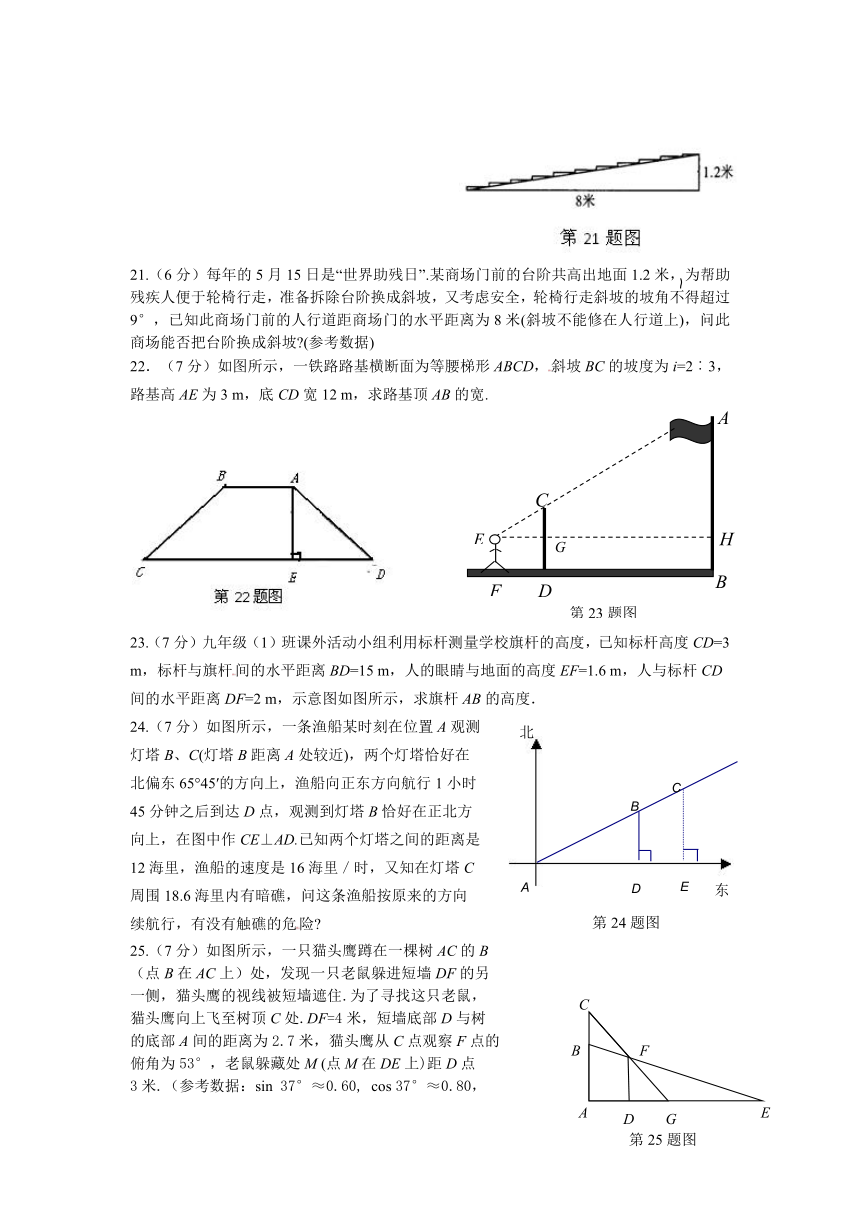
21.(6分)每年的5月15日是“世界助残日”.某商场门前的台阶共高出地面1.2米,为帮助残疾人便于轮椅行走,准备拆除台阶换成斜坡,又考虑安全,轮椅行走斜坡的坡角不得超过9°,已知此商场门前的人行道距商场门的水平距离为8米(斜坡不能修在人行道上),问此商场能否把台阶换成斜坡 (参考数据)
22.(7分)如图所示,一铁路路基横断面为等腰梯形ABCD,斜坡BC的坡度为i=2︰3,路基高AE为3 m,底CD宽12 m,求路基顶AB的宽.
23.(7分)九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度CD=3 m,标杆与旗杆间的水平距离BD=15 m,人的眼睛与地面的高度EF=1.6 m,人与标杆CD间的水平距离DF=2 m,示意图如图所示,求旗杆AB的高度.
24.(7分)如图所示,一条渔船某时刻在位置A观测
灯塔B、C(灯塔B距离A处较近),两个灯塔恰好在
北偏东65°45′的方向上,渔船向正东方向航行1小时
45分钟之后到达D点,观测到灯塔B恰好在正北方
向上,在图中作CE⊥AD.已知两个灯塔之间的距离是
12海里,渔船的速度是16海里/时,又知在灯塔C
周围18.6海里内有暗礁,问这条渔船按原来的方向
续航行,有没有触礁的危险
25.(7分)如图所示,一只猫头鹰蹲在一棵树AC的B
(点B在AC上)处,发现一只老鼠躲进短墙DF的另
一侧,猫头鹰的视线被短墙遮住.为了寻找这只老鼠,
猫头鹰向上飞至树顶C处.DF=4米,短墙底部D与树
的底部A间的距离为2.7米,猫头鹰从C点观察F点的
俯角为53°,老鼠躲藏处M (点M在DE上)距D点
3米.(参考数据:sin 37°≈0.60, cos 37°≈0.80,
tan 37°≈0.75)
(1)猫头鹰飞至C处后,能否看到这只老鼠?为什么?
(2)要捕捉到这只老鼠,猫头鹰至少要飞多少米(精确到0.1米)?
第七章 锐角三角函数检测题参考答案
一、选择题
1.C 解析:由于在直角三角形中锐角A的正弦值是对边和斜边的比,余弦值是邻边和斜边的比,所以边长同时扩大2倍对于锐角A的正弦值和余弦值没有影响,由此即可确定选项C正确.
2.A 解析:在Rt△ABC中,∠C=90°,∵ BC=4,sin A=,∴ AB=BC÷sin A=5,AC==3.
3.A 解析:∵ sin 30°=,,∴ 0°<∠A<30°.故选A.
4.D 解析:因为可设∠A的邻边长为k(k>0),则斜边长为3k,所以∠A的对边长为.所以,.所以原式==0.
5.B 解析:设∠A、∠B、∠C的度数分别为、、2,则 =180°,解得=45°.
∴ 2=90°.∴ ∠A、∠B、∠C的度数分别为45°、45°、90°.∴ △ABC是等腰直角三角形,∴ =1︰1︰.
6.B 解析:设∠A、∠B、∠C 的对边分别为a、b、c,
A.sin A=,sin B=,sin A≠sin B,故错误;B.cos B=,sin A=cos B,故正确;
C.tan A=,tan B=,tan A≠tan B,故错误;D.,则≠tan B,故错误.
7.B 解析:设小球距离地面的高度为则小球水平移动的距离为 所以解得
8.A 解析:∵ sin 60°=,cos 60°=,∴(-sin 60°,cos 60°)=(,),
∴ 关于y轴对称的点的坐标为(,).故选A.
9.B 解析:由于某同学站在离国旗旗杆12米远的地方,当国旗升起到旗杆顶时,他测得视线的仰角为30°,则目高以上旗杆的高度h1=12×tan 30°=4(米),旗杆的高度h=h1+1.6=1.6+4≈8.5(米).故选B.
10.D 解析:设经过A地正西方向上的D点,则AD=AB sin 60°=50 (m),BD=AB cos 60°=50(m),∴ CD=150(m). ∴ AC==100 (m).故选D.
二、填空题
11. 解析:sin B==.
12. 解析:在△ABC中,∵ AC=3,BC=,AB=,∴=32,即,∴ △ABC是直角三角形,且∠B=90°.∴ cos A==.
13. 解析:连接PP',过点B作BD⊥PP',交PP'于点D,因为∠PBP'=30°,所以∠PBD=15°,利用sin 15°=,先求出PD,乘2即得PP'.
14.48 解析:根据两直线平行,内错角相等进行判断.
15.(0,) 解析:过点B作BC⊥AO,交AO于点C,利用勾股定理或锐角三角函数可分别求得AC与OC的长,即可确定点A的坐标.
16. 解析:利用网格,从C点向AB所在直线作垂线,利用勾股定理得,所以.
17. 解析:先根据勾股定理求得AC=5,再根据求出结果.
18.4.86 解析:利用正切函数的定义分别求出BD,BC的长.
三、解答题
19.解:原式==-1.
20.(1)证明:在Rt△ABD中,有.
在 Rt△ADC中,有.
(2)解:由,可设,
由勾股定理求得.
即 ,
21.解:因为所以斜坡的坡角小于9°,
故此商场能把台阶换成斜坡.
22.解:过B作BFCD,垂足为F,∴
在等腰梯形ABCD中,AD=BC,.
∵ BF︰CF=2︰3,BF =AE=3 m,∴CF =4.5 m.
AD=BC,,∠CFB=∠DEA=90°,∴ △BCF≌△ADE.
∴DE=CF= 4.5 m. ∴ EF=CD-CF-DE=3 m.
,∴ BF//AE. ∴ 四边形ABFE为平行四边形.
AB=EF=3 m.
23.解:,,.
.
,即.
,.
.
24.解:在Rt △ABD中,(海里),
∠BAD=90°-65°45′=24°15′.
∵ cos 24°15′=,∴ (海里).
AC=AB+BC≈30.71+12=42.71(海里).
在Rt △ACE中,sin 24°15′=,
∴ CE=AC·sin 24°15′≈42.71×0.410 7≈17.54(海里).
∵ 17.54<18.6,∴ 有触礁危险.
答:继续航行有触礁危险.
25.解:(1)由已知可得∠DFG=∠C=37°.
在Rt△DFG中,DG=DF·tan 37°≈4×0.75=3(米).
因此,猫头鹰能看到这只老鼠.
(2)AG=AD+DG≈2.7+3=5.7(米),
在Rt△ACG中,CG=≈9.5(米).
答:猫头鹰至少要飞9.5米.
第13题图
北
甲
北
乙
第14题图
x
O
A
y
B
第15题图
A
40°
52 m
C
D
B
43°¤
第18题图
第20题图
第23题图
G
E
A
C
B
D
北
东
第24题图
C
F
B
A
D
G
E
第25题图
【本检测题满分:100分,时间90分钟】
一、选择题(每小题3分,共30分)
1.在直角三角形中,各边都扩大2倍,则锐角A的正弦值与余弦值都( )
A.缩小2倍 B.扩大2倍 C.不变 D.不能确定
2.在Rt△ABC中,∠C=,BC=4,sin A=,则AC=( )
A.3 B.4 C.5 D.6
3.若∠A是锐角,且sin A=,则( )
A.<∠A< B.<∠A< C.<∠A< D.<∠A<
4.若cos A=,则=( )
A. B. C. D.0
5.在△ABC中,∠A︰∠B︰∠C=1︰1︰2,则=( )
A.1︰1︰2 B. 1︰1︰ C. 1︰1︰ D. 1︰1︰
6.在Rt△ABC中,∠C=,则下列式子成立的是( )
A.sin A=sin B B.sin A=cos B
C.tan A=tan B D.cos A=tan B
7.如图,一个小球由地面沿着坡度的坡面向上前进了10 m,此时小球距离地面的高度为( )
A. B.2 m C.4 m D.m
8.点(-sin 60°,cos 60°)关于y轴对称的点的坐标是( )
A.(,) B.(,) C.(,) D.(,)
9.每周一学校都要举行庄严的升国旗仪式,让我们感受到了国旗的神圣.某同学站在离旗杆12米远的地方,当国旗升起到旗杆顶时,他测得视线的仰角为30°,若这位同学的目高为1.6米,则旗杆的高度约为( )
A.6.9米 B.8.5米 C.10.3米 D.12.0米
10.王英同学从A地沿北偏西60°方向走100 m到B地,再从B地向正南方向走200 m到C地,此时王英同学离A地 ( )
A.50 m B.100 m C.150 m D.100 m
二、填空题(每小题3分,共24分)
11.在Rt△ABC中,∠C=90°,AB=5,AC=3,则sin B=_____.
12.在△ABC中,若BC=,AB=,AC=3,则cos A=________.
13.如图所示,如果△APB绕点B按逆时针方向旋转30°后得到△A'P'B,且BP=2,那么点P与点P'间的长度为___________. (不取近似值. 以下数据供解题使用:sin 15°=,cos 15°=)
14.如图所示,在甲、乙两地之间修一条笔直的公路,从甲地测得公路的走向是北偏东48°.甲、乙两地同时开工,若干天后,公路准确接通,则乙地所修公路的走向是南偏西_________度.
15.如图所示,机器人从A点沿着西南方向行了4个单位,到达B点后观察到原点O在它的南偏东60°的方向上,则原来A点的坐标为___________(结果保留根号).
16.如图所示,△ABC的顶点都在方格纸的格点上,则_ .
17.在直角三角形ABC中,∠A=90°,BC=13,AB=12,那么
___________.
18.根据图中所给的数据,求得避雷针CD的长约为__m
(结果精确到0.01 m).(可用计算器求,也可用下列参考
数据求:sin ≈0.682 0,sin 40°≈0.642 8,
cos 43°≈0.731 4,cos 40°≈0.766 0,tan 43°
≈0.932 5,tan 40°≈0.839 1)
三、解答题(共46分)
19.(6分)计算:.
20.(6分)如图所示,在△ABC中,AD是BC边上的高,
.
(1)求证:AC=BD;
(2)若,求AD的长.
21.(6分)每年的5月15日是“世界助残日”.某商场门前的台阶共高出地面1.2米,为帮助残疾人便于轮椅行走,准备拆除台阶换成斜坡,又考虑安全,轮椅行走斜坡的坡角不得超过9°,已知此商场门前的人行道距商场门的水平距离为8米(斜坡不能修在人行道上),问此商场能否把台阶换成斜坡 (参考数据)
22.(7分)如图所示,一铁路路基横断面为等腰梯形ABCD,斜坡BC的坡度为i=2︰3,路基高AE为3 m,底CD宽12 m,求路基顶AB的宽.
23.(7分)九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度CD=3 m,标杆与旗杆间的水平距离BD=15 m,人的眼睛与地面的高度EF=1.6 m,人与标杆CD间的水平距离DF=2 m,示意图如图所示,求旗杆AB的高度.
24.(7分)如图所示,一条渔船某时刻在位置A观测
灯塔B、C(灯塔B距离A处较近),两个灯塔恰好在
北偏东65°45′的方向上,渔船向正东方向航行1小时
45分钟之后到达D点,观测到灯塔B恰好在正北方
向上,在图中作CE⊥AD.已知两个灯塔之间的距离是
12海里,渔船的速度是16海里/时,又知在灯塔C
周围18.6海里内有暗礁,问这条渔船按原来的方向
续航行,有没有触礁的危险
25.(7分)如图所示,一只猫头鹰蹲在一棵树AC的B
(点B在AC上)处,发现一只老鼠躲进短墙DF的另
一侧,猫头鹰的视线被短墙遮住.为了寻找这只老鼠,
猫头鹰向上飞至树顶C处.DF=4米,短墙底部D与树
的底部A间的距离为2.7米,猫头鹰从C点观察F点的
俯角为53°,老鼠躲藏处M (点M在DE上)距D点
3米.(参考数据:sin 37°≈0.60, cos 37°≈0.80,
tan 37°≈0.75)
(1)猫头鹰飞至C处后,能否看到这只老鼠?为什么?
(2)要捕捉到这只老鼠,猫头鹰至少要飞多少米(精确到0.1米)?
第七章 锐角三角函数检测题参考答案
一、选择题
1.C 解析:由于在直角三角形中锐角A的正弦值是对边和斜边的比,余弦值是邻边和斜边的比,所以边长同时扩大2倍对于锐角A的正弦值和余弦值没有影响,由此即可确定选项C正确.
2.A 解析:在Rt△ABC中,∠C=90°,∵ BC=4,sin A=,∴ AB=BC÷sin A=5,AC==3.
3.A 解析:∵ sin 30°=,,∴ 0°<∠A<30°.故选A.
4.D 解析:因为可设∠A的邻边长为k(k>0),则斜边长为3k,所以∠A的对边长为.所以,.所以原式==0.
5.B 解析:设∠A、∠B、∠C的度数分别为、、2,则 =180°,解得=45°.
∴ 2=90°.∴ ∠A、∠B、∠C的度数分别为45°、45°、90°.∴ △ABC是等腰直角三角形,∴ =1︰1︰.
6.B 解析:设∠A、∠B、∠C 的对边分别为a、b、c,
A.sin A=,sin B=,sin A≠sin B,故错误;B.cos B=,sin A=cos B,故正确;
C.tan A=,tan B=,tan A≠tan B,故错误;D.,则≠tan B,故错误.
7.B 解析:设小球距离地面的高度为则小球水平移动的距离为 所以解得
8.A 解析:∵ sin 60°=,cos 60°=,∴(-sin 60°,cos 60°)=(,),
∴ 关于y轴对称的点的坐标为(,).故选A.
9.B 解析:由于某同学站在离国旗旗杆12米远的地方,当国旗升起到旗杆顶时,他测得视线的仰角为30°,则目高以上旗杆的高度h1=12×tan 30°=4(米),旗杆的高度h=h1+1.6=1.6+4≈8.5(米).故选B.
10.D 解析:设经过A地正西方向上的D点,则AD=AB sin 60°=50 (m),BD=AB cos 60°=50(m),∴ CD=150(m). ∴ AC==100 (m).故选D.
二、填空题
11. 解析:sin B==.
12. 解析:在△ABC中,∵ AC=3,BC=,AB=,∴=32,即,∴ △ABC是直角三角形,且∠B=90°.∴ cos A==.
13. 解析:连接PP',过点B作BD⊥PP',交PP'于点D,因为∠PBP'=30°,所以∠PBD=15°,利用sin 15°=,先求出PD,乘2即得PP'.
14.48 解析:根据两直线平行,内错角相等进行判断.
15.(0,) 解析:过点B作BC⊥AO,交AO于点C,利用勾股定理或锐角三角函数可分别求得AC与OC的长,即可确定点A的坐标.
16. 解析:利用网格,从C点向AB所在直线作垂线,利用勾股定理得,所以.
17. 解析:先根据勾股定理求得AC=5,再根据求出结果.
18.4.86 解析:利用正切函数的定义分别求出BD,BC的长.
三、解答题
19.解:原式==-1.
20.(1)证明:在Rt△ABD中,有.
在 Rt△ADC中,有.
(2)解:由,可设,
由勾股定理求得.
即 ,
21.解:因为所以斜坡的坡角小于9°,
故此商场能把台阶换成斜坡.
22.解:过B作BFCD,垂足为F,∴
在等腰梯形ABCD中,AD=BC,.
∵ BF︰CF=2︰3,BF =AE=3 m,∴CF =4.5 m.
AD=BC,,∠CFB=∠DEA=90°,∴ △BCF≌△ADE.
∴DE=CF= 4.5 m. ∴ EF=CD-CF-DE=3 m.
,∴ BF//AE. ∴ 四边形ABFE为平行四边形.
AB=EF=3 m.
23.解:,,.
.
,即.
,.
.
24.解:在Rt △ABD中,(海里),
∠BAD=90°-65°45′=24°15′.
∵ cos 24°15′=,∴ (海里).
AC=AB+BC≈30.71+12=42.71(海里).
在Rt △ACE中,sin 24°15′=,
∴ CE=AC·sin 24°15′≈42.71×0.410 7≈17.54(海里).
∵ 17.54<18.6,∴ 有触礁危险.
答:继续航行有触礁危险.
25.解:(1)由已知可得∠DFG=∠C=37°.
在Rt△DFG中,DG=DF·tan 37°≈4×0.75=3(米).
因此,猫头鹰能看到这只老鼠.
(2)AG=AD+DG≈2.7+3=5.7(米),
在Rt△ACG中,CG=≈9.5(米).
答:猫头鹰至少要飞9.5米.
第13题图
北
甲
北
乙
第14题图
x
O
A
y
B
第15题图
A
40°
52 m
C
D
B
43°¤
第18题图
第20题图
第23题图
G
E
A
C
B
D
北
东
第24题图
C
F
B
A
D
G
E
第25题图
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
