甘肃省定西市临洮县文峰中学2021-2022学年高二下学期期中考试数学(理)试题(Word版含答案)
文档属性
| 名称 | 甘肃省定西市临洮县文峰中学2021-2022学年高二下学期期中考试数学(理)试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 433.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-14 13:07:59 | ||
图片预览



文档简介
文峰中学2021-2022学年高二下学期期中考试
理科数学
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.集合则等于( )
A. B. C. D.
2.则z的值为( )
A. B. C. D.
3.某种包装的大米质量(单位:kg)服从正态分布,根据检测结果可知
P(9.98≤≤10.02)=0.98,某公司购买该种包装的大米2000袋,则大米质量在10.02kg以上的袋数大约为( )
A、10 B. 20 C. 30 D. 40
4.已知向量,,,若,则实数的值为( )
A. B. C. D.
5.设为等差数列的前项和,若,,则( )
A. B. C. D.
6.第24届冬季奥运会于2022年2月4日至20日在北京举行,中国代表团取得了9枚金牌,4枚银牌,2枚铜牌的历史最好成绩.2月8日,在自由式滑雪女子大跳台坡面障碍技巧比赛中,中国运动员谷爱凌在最后一跳中完美地完成了超高难度动作1620,得分反超对手,获得了金牌.已知六个裁判为谷爱凌这一跳的打分分别为95,95,95,93,94,94,评分规则为去掉六个原始分中的一个最高分和一个最低分,剩下四个有效分的平均数即为该选手的本轮得分.设这六个原始分的中位数为,方差为;四个有效分的中位数为,方差为.则下列结论正确的是( )
A. B. C. D.
7.某学校为了更好地培养尖子生,使其全面发展,决定由3名教师对5个尖子生进行“包教”,要求每名教师的“包教”学生不超过2人,则不同的“包教”方案有( )
A.60 B.90 C.150 D.120
8.先后两次抛掷一枚质地均匀的骰子,观察它落地时朝上的面的点数,则第一次点数大于第二次点数的概率为( )
A. B. C. D.
9.双曲线(a>0,b>0)的两个焦点为,若P为其上的一点,且,则双曲线离心率的取值范围为( )
A. B. C. D.
10.将函数的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得图像向左平移个单位,则所得函数图像对应的解析式为( )
A. B. C. D.
11.三棱锥中,平面,则该三棱锥外接球的表面积为( )
A. B. C. D.
12.已知是边长为2的等边三角形,P为平面ABC内一点,则的最小是( )
A. B. C. D.
二、填空题:本题共4小题,每题5分,共20分.
13.已知随机变量满足,若则 .
14. 在的展开式中,的系数为 .
15.若直线为曲线的一条切线,则实数的值是_______。
16.已知等差数列的前n项和为,并且, ,若对恒成立,则正整数的值为______.
三、解答题:共70分.解答应写出文字说明,证明过程或演算步骤.
17.己知分别为三个内角A,B,C的对边,且.
(I)求角A的大小;
(II)若b+c=5,且的面积为,求a的值.
18.已知三棱锥P—ABC(如图1)的平面展开图(如图2)中,四边形ABCD(P)为边长为的正方形,和均为正三角形,在三棱锥中:
(I)求点P到平面ABC的距离.
(II)求二面角A—PC—B的余弦值.
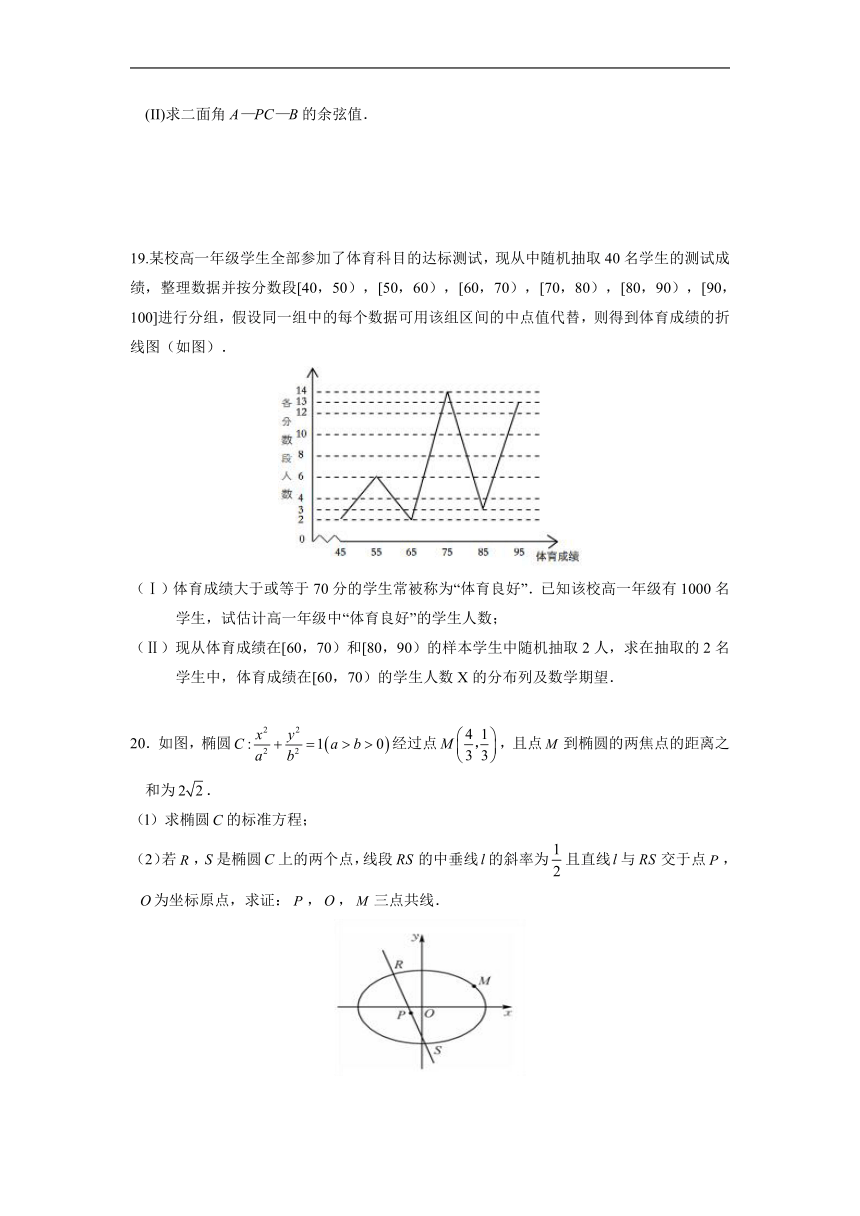
19.某校高一年级学生全部参加了体育科目的达标测试,现从中随机抽取40名学生的测试成绩,整理数据并按分数段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]进行分组,假设同一组中的每个数据可用该组区间的中点值代替,则得到体育成绩的折线图(如图).
(Ⅰ)体育成绩大于或等于70分的学生常被称为“体育良好”.已知该校高一年级有1000名学生,试估计高一年级中“体育良好”的学生人数;
(Ⅱ)现从体育成绩在[60,70)和[80,90)的样本学生中随机抽取2人,求在抽取的2名学生中,体育成绩在[60,70)的学生人数X的分布列及数学期望.
20.如图,椭圆经过点,且点到椭圆的两焦点的距离之和为.
(l)求椭圆的标准方程;
(2)若,是椭圆上的两个点,线段的中垂线的斜率为且直线与交于点,为坐标原点,求证:,,三点共线.
21.已知函数.
(1)若,求函数的值域.
(2)若函数在上是减函数,求实数的取值范围;
选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.
22.选修4-4:坐标系与参数方程
在平面直角坐标系中,已知直线的参数方程为 (为参数),以坐标原点为极点,以轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为,直线与曲线C交于A,B两点
(1)求直线l的普通方程和曲线的直角坐标方程;
(2)已知点的极坐标为,求的值.
23.[选修4–5:不等式选讲]
已知.
(1)当时,求不等式的解集;
(2)若时不等式成立,求的取值范围.
理科数学参考答案
一、选择题:
CCBA BDBA ADCB
二、填空题
13.2; 14. 6; 15.1 16.5
三、解答题
17.解:(Ⅰ)由正弦定理得,
∵
∴ ,即.
∵∴
∴ ∴.
(Ⅱ)由: 可得.
∴
∵
∴由余弦定理得:
∴
18.(Ⅰ)解:设的中点为,连接,.
由题意得,
,,,
因为在中,,为的中点,
所以,
因为在中,,,,
所以,
因为,平面,
所以平面,
即PO就是点P到平面ABC的距离,
所以点P到平面ABC的距离为1.
(Ⅱ)解:由平面,,如图建立空间直角坐标系,则
,,,,.
由平面,故平面的法向量为,
由,,
设平面的法向量为,则
由得:
令,得,,即,
.
由二面角是锐二面角,
所以二面角的余弦值为.
19.解:(Ⅰ)由折线图知,样本中体育成绩大于或等于70分的学生有30人
所以该校高一年级学生中,“体育良好”的学生人数大约为人
(Ⅱ)的分布列为:
X 0 1 2
P
20.解:(1)因为点到椭圆的两焦点的距离之和为,
所以,解得.
又椭圆经过点,所以.
所以.所以椭圆的标准方程为.
(2)因为线段的中垂线的斜率为,
所以直线的斜率为.所以可设直线的方程为.
据得,
设点,,,
所以,,
所以,,
因为,所以,
所以点在直线上,
又点,也在直线上,
所以,,三点共线.
21.解:(1)当时,
在上单调递减,在上单调递增
即的值域为.
(2)由函数在上是减函数,知恒成立,
.
由恒成立可知恒成立,则,
设,则,
由,知,
函数在上递增,在上递减,
∴,∴.
22.解:(1) 的普通方程为: ;
又,
即曲线的直角坐标方程为:
(2)解法一: 在直线上,直线的参数方程为(为参数),代入曲线的直角坐标方程得,即,
.
解法二:
,
,,
23.解:(1)当时,,即
故不等式的解集为.
(2)当时成立等价于当时成立.
若,则当时;
若,的解集为,所以,故.
综上,的取值范围为.
理科数学
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.集合则等于( )
A. B. C. D.
2.则z的值为( )
A. B. C. D.
3.某种包装的大米质量(单位:kg)服从正态分布,根据检测结果可知
P(9.98≤≤10.02)=0.98,某公司购买该种包装的大米2000袋,则大米质量在10.02kg以上的袋数大约为( )
A、10 B. 20 C. 30 D. 40
4.已知向量,,,若,则实数的值为( )
A. B. C. D.
5.设为等差数列的前项和,若,,则( )
A. B. C. D.
6.第24届冬季奥运会于2022年2月4日至20日在北京举行,中国代表团取得了9枚金牌,4枚银牌,2枚铜牌的历史最好成绩.2月8日,在自由式滑雪女子大跳台坡面障碍技巧比赛中,中国运动员谷爱凌在最后一跳中完美地完成了超高难度动作1620,得分反超对手,获得了金牌.已知六个裁判为谷爱凌这一跳的打分分别为95,95,95,93,94,94,评分规则为去掉六个原始分中的一个最高分和一个最低分,剩下四个有效分的平均数即为该选手的本轮得分.设这六个原始分的中位数为,方差为;四个有效分的中位数为,方差为.则下列结论正确的是( )
A. B. C. D.
7.某学校为了更好地培养尖子生,使其全面发展,决定由3名教师对5个尖子生进行“包教”,要求每名教师的“包教”学生不超过2人,则不同的“包教”方案有( )
A.60 B.90 C.150 D.120
8.先后两次抛掷一枚质地均匀的骰子,观察它落地时朝上的面的点数,则第一次点数大于第二次点数的概率为( )
A. B. C. D.
9.双曲线(a>0,b>0)的两个焦点为,若P为其上的一点,且,则双曲线离心率的取值范围为( )
A. B. C. D.
10.将函数的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得图像向左平移个单位,则所得函数图像对应的解析式为( )
A. B. C. D.
11.三棱锥中,平面,则该三棱锥外接球的表面积为( )
A. B. C. D.
12.已知是边长为2的等边三角形,P为平面ABC内一点,则的最小是( )
A. B. C. D.
二、填空题:本题共4小题,每题5分,共20分.
13.已知随机变量满足,若则 .
14. 在的展开式中,的系数为 .
15.若直线为曲线的一条切线,则实数的值是_______。
16.已知等差数列的前n项和为,并且, ,若对恒成立,则正整数的值为______.
三、解答题:共70分.解答应写出文字说明,证明过程或演算步骤.
17.己知分别为三个内角A,B,C的对边,且.
(I)求角A的大小;
(II)若b+c=5,且的面积为,求a的值.
18.已知三棱锥P—ABC(如图1)的平面展开图(如图2)中,四边形ABCD(P)为边长为的正方形,和均为正三角形,在三棱锥中:
(I)求点P到平面ABC的距离.
(II)求二面角A—PC—B的余弦值.
19.某校高一年级学生全部参加了体育科目的达标测试,现从中随机抽取40名学生的测试成绩,整理数据并按分数段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]进行分组,假设同一组中的每个数据可用该组区间的中点值代替,则得到体育成绩的折线图(如图).
(Ⅰ)体育成绩大于或等于70分的学生常被称为“体育良好”.已知该校高一年级有1000名学生,试估计高一年级中“体育良好”的学生人数;
(Ⅱ)现从体育成绩在[60,70)和[80,90)的样本学生中随机抽取2人,求在抽取的2名学生中,体育成绩在[60,70)的学生人数X的分布列及数学期望.
20.如图,椭圆经过点,且点到椭圆的两焦点的距离之和为.
(l)求椭圆的标准方程;
(2)若,是椭圆上的两个点,线段的中垂线的斜率为且直线与交于点,为坐标原点,求证:,,三点共线.
21.已知函数.
(1)若,求函数的值域.
(2)若函数在上是减函数,求实数的取值范围;
选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.
22.选修4-4:坐标系与参数方程
在平面直角坐标系中,已知直线的参数方程为 (为参数),以坐标原点为极点,以轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为,直线与曲线C交于A,B两点
(1)求直线l的普通方程和曲线的直角坐标方程;
(2)已知点的极坐标为,求的值.
23.[选修4–5:不等式选讲]
已知.
(1)当时,求不等式的解集;
(2)若时不等式成立,求的取值范围.
理科数学参考答案
一、选择题:
CCBA BDBA ADCB
二、填空题
13.2; 14. 6; 15.1 16.5
三、解答题
17.解:(Ⅰ)由正弦定理得,
∵
∴ ,即.
∵∴
∴ ∴.
(Ⅱ)由: 可得.
∴
∵
∴由余弦定理得:
∴
18.(Ⅰ)解:设的中点为,连接,.
由题意得,
,,,
因为在中,,为的中点,
所以,
因为在中,,,,
所以,
因为,平面,
所以平面,
即PO就是点P到平面ABC的距离,
所以点P到平面ABC的距离为1.
(Ⅱ)解:由平面,,如图建立空间直角坐标系,则
,,,,.
由平面,故平面的法向量为,
由,,
设平面的法向量为,则
由得:
令,得,,即,
.
由二面角是锐二面角,
所以二面角的余弦值为.
19.解:(Ⅰ)由折线图知,样本中体育成绩大于或等于70分的学生有30人
所以该校高一年级学生中,“体育良好”的学生人数大约为人
(Ⅱ)的分布列为:
X 0 1 2
P
20.解:(1)因为点到椭圆的两焦点的距离之和为,
所以,解得.
又椭圆经过点,所以.
所以.所以椭圆的标准方程为.
(2)因为线段的中垂线的斜率为,
所以直线的斜率为.所以可设直线的方程为.
据得,
设点,,,
所以,,
所以,,
因为,所以,
所以点在直线上,
又点,也在直线上,
所以,,三点共线.
21.解:(1)当时,
在上单调递减,在上单调递增
即的值域为.
(2)由函数在上是减函数,知恒成立,
.
由恒成立可知恒成立,则,
设,则,
由,知,
函数在上递增,在上递减,
∴,∴.
22.解:(1) 的普通方程为: ;
又,
即曲线的直角坐标方程为:
(2)解法一: 在直线上,直线的参数方程为(为参数),代入曲线的直角坐标方程得,即,
.
解法二:
,
,,
23.解:(1)当时,,即
故不等式的解集为.
(2)当时成立等价于当时成立.
若,则当时;
若,的解集为,所以,故.
综上,的取值范围为.
同课章节目录
