不等式及解集[下学期]
图片预览




文档简介
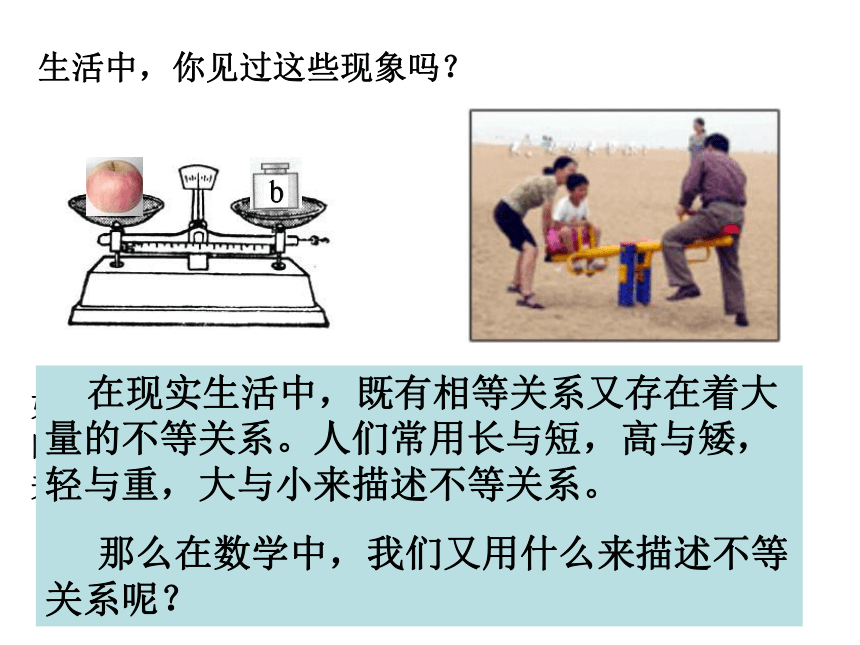
课件16张PPT。生活中,你见过这些现象吗?如图所示,你知道苹果的重量a与砝码重量b的关系吗?a=b如果母亲放开手,你说会出现怎样的结果呢?你能解释这种现象吗?M>m 在现实生活中,既有相等关系又存在着大量的不等关系。人们常用长与短,高与矮,轻与重,大与小来描述不等关系。
那么在数学中,我们又用什么来描述不等关系呢?你能用适当的式子表示下列问题中的数量关系吗?1、0大于-5;
2、y的2倍比6小;
3、x与3的差大于-1;
4、x2减去10是正数;
5、a的倒数小于2。0>-52y<6X-3 >-1X2-10 >0像这些用不等号表示大小关系的式子叫做不等式。 类似于一元一次方程,我们把含有一个未知数,未知数的次数是1的不等式叫做一元一次不等式。X>50 虽然这些不等式明确表示了车速应满足的条件,但我们希望更明确得出x应取哪些值. 与方程类似,我们把使不等式成立的未知数的值叫做不等式的解. 你认为车速可以是60千米/小时吗?可以是75千米/小时吗?可以是80千米/小时吗?你是怎样思考的?
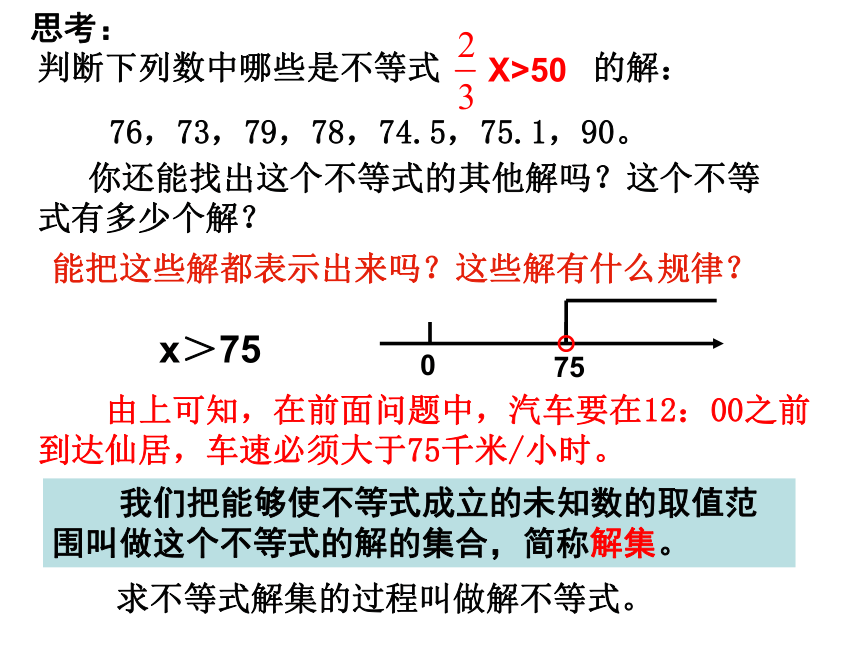
在这里,80是不等式 的解,60和75不是不等式 的解思考:76,73,79,78,74.5,75.1,90。 你还能找出这个不等式的其他解吗?这个不等式有多少个解?能把这些解都表示出来吗?这些解有什么规律?x>75求不等式解集的过程叫做解不等式。 由上可知,在前面问题中,汽车要在12:00之前到达仙居,车速必须大于75千米/小时。 我们把能够使不等式成立的未知数的取值范围叫做这个不等式的解的集合,简称解集。巩固练习:1、下列各式中,哪些是一元一次不等式?
(1)-3>-5 (2)x>1
(3)2x+y<6 (4)2-x<3x+5
(5)3x+1=0 (6)2、下列数哪些是不等式3X>6的解?哪些不是?
-4,-2.5,0,1,2.5,3,3.2,4.8,8,12。Bx<2x>2x≤2x≥24、图中红色部分所表示的是哪些数?你能用不等式表示这个区域吗?0-115、请说出一个不等式,使得3是它的一个解,而4不是它的解。6、请直接想出下列不等式的解集,并在数轴上表示。
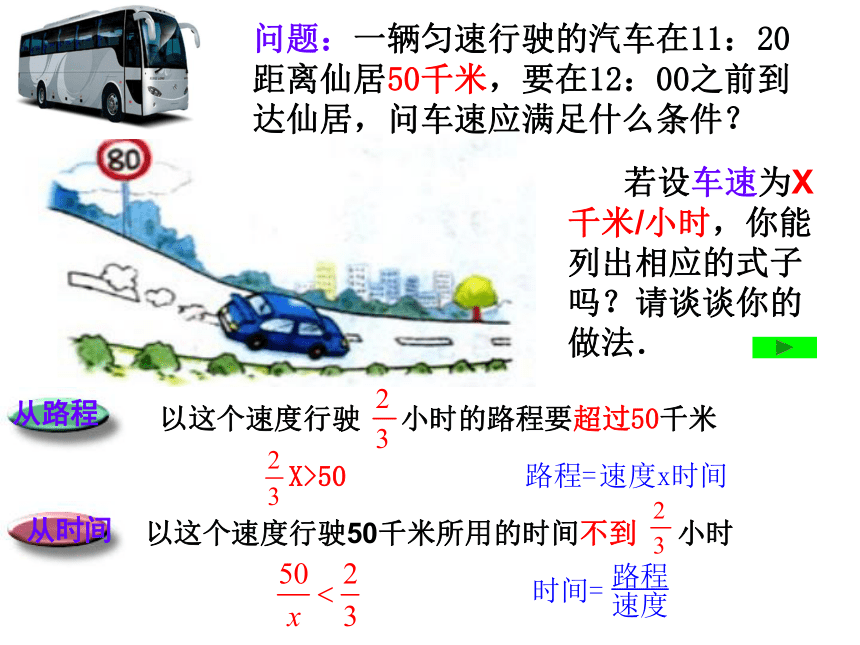
(1) 2x<8 (2)x-2>0X<1问题1:一辆匀速行驶的汽车在11:20距离仙居50千米,要在12:00之前到达仙居,问车速应满足什么条件?问题2:一辆匀速行驶的汽车在11:20距离仙居50千米,要在12:00准时到达仙居,问车速应满足什么条件?这两个问题有什么不同?问题的深入 方程刻画某个变化过程中的一瞬间,不等式可以刻画变化过程中的一个范围.原问题:一辆匀速行驶的汽车在11:20距离仙居50千米,要在12:00之前到达仙居,问车速应满足什么条件? 在原问题的解决中,我们已经得出汽车要在12:00之前到达仙居,车速必须大于75千米/小时。
如果注意到路边的限速标记,则车速又应满足什么条件?如何用不等式表示这个速度?如何在数轴上表示这个范围?这是什么?或回顾与小结:1、本节思路2、本节的思想方法(1)类比的思想 等量与不等量;等式与不等式;方程的解与不等式的解;一元一次方程与一元一次不等式
(2)数形结合的思想 数轴与不等式的解集
不等式x<5有多少个解?有多少个正整数解?补充题1:
不等式x<5有无数个解;有4个正整数解,分别是4,3,2,1。补充题2: 当x为任何正数时,都能使不等式x+3>2成立,能不能说不等式x+3>2的解集是x>0?为什么? 世纪公园的票价是:每人5元;一次购票满30张,每张可少收1元。某班有27名少先队员去世纪公园进行活动。当领队王小华准备好了零钱到售票处买27张票时,爱动脑筋的李敏同学喊住了王小华,提议买30张票。你认为李敏的提议有道理吗,为什么?至少要有多少人去世纪公园,多买票反而合算呢? 补充题3:X>50 虽然这个不等式明确表示了车速应满足的条件,但我们希望更明确得出x应取哪些值. 与方程类似,我们把使不等式成立的未知数的值叫做不等式的解. 你认为车速可以是60千米/小时吗?可以是75千米/小时吗?可以是80千米/小时吗?你是怎样思考的?
在这里,80是不等式 的解,60和75不是不等式 的解
那么在数学中,我们又用什么来描述不等关系呢?你能用适当的式子表示下列问题中的数量关系吗?1、0大于-5;
2、y的2倍比6小;
3、x与3的差大于-1;
4、x2减去10是正数;
5、a的倒数小于2。0>-52y<6X-3 >-1X2-10 >0像这些用不等号表示大小关系的式子叫做不等式。 类似于一元一次方程,我们把含有一个未知数,未知数的次数是1的不等式叫做一元一次不等式。X>50 虽然这些不等式明确表示了车速应满足的条件,但我们希望更明确得出x应取哪些值. 与方程类似,我们把使不等式成立的未知数的值叫做不等式的解. 你认为车速可以是60千米/小时吗?可以是75千米/小时吗?可以是80千米/小时吗?你是怎样思考的?
在这里,80是不等式 的解,60和75不是不等式 的解思考:76,73,79,78,74.5,75.1,90。 你还能找出这个不等式的其他解吗?这个不等式有多少个解?能把这些解都表示出来吗?这些解有什么规律?x>75求不等式解集的过程叫做解不等式。 由上可知,在前面问题中,汽车要在12:00之前到达仙居,车速必须大于75千米/小时。 我们把能够使不等式成立的未知数的取值范围叫做这个不等式的解的集合,简称解集。巩固练习:1、下列各式中,哪些是一元一次不等式?
(1)-3>-5 (2)x>1
(3)2x+y<6 (4)2-x<3x+5
(5)3x+1=0 (6)2、下列数哪些是不等式3X>6的解?哪些不是?
-4,-2.5,0,1,2.5,3,3.2,4.8,8,12。Bx<2x>2x≤2x≥24、图中红色部分所表示的是哪些数?你能用不等式表示这个区域吗?0-115、请说出一个不等式,使得3是它的一个解,而4不是它的解。6、请直接想出下列不等式的解集,并在数轴上表示。
(1) 2x<8 (2)x-2>0X<1问题1:一辆匀速行驶的汽车在11:20距离仙居50千米,要在12:00之前到达仙居,问车速应满足什么条件?问题2:一辆匀速行驶的汽车在11:20距离仙居50千米,要在12:00准时到达仙居,问车速应满足什么条件?这两个问题有什么不同?问题的深入 方程刻画某个变化过程中的一瞬间,不等式可以刻画变化过程中的一个范围.原问题:一辆匀速行驶的汽车在11:20距离仙居50千米,要在12:00之前到达仙居,问车速应满足什么条件? 在原问题的解决中,我们已经得出汽车要在12:00之前到达仙居,车速必须大于75千米/小时。
如果注意到路边的限速标记,则车速又应满足什么条件?如何用不等式表示这个速度?如何在数轴上表示这个范围?这是什么?或回顾与小结:1、本节思路2、本节的思想方法(1)类比的思想 等量与不等量;等式与不等式;方程的解与不等式的解;一元一次方程与一元一次不等式
(2)数形结合的思想 数轴与不等式的解集
不等式x<5有多少个解?有多少个正整数解?补充题1:
不等式x<5有无数个解;有4个正整数解,分别是4,3,2,1。补充题2: 当x为任何正数时,都能使不等式x+3>2成立,能不能说不等式x+3>2的解集是x>0?为什么? 世纪公园的票价是:每人5元;一次购票满30张,每张可少收1元。某班有27名少先队员去世纪公园进行活动。当领队王小华准备好了零钱到售票处买27张票时,爱动脑筋的李敏同学喊住了王小华,提议买30张票。你认为李敏的提议有道理吗,为什么?至少要有多少人去世纪公园,多买票反而合算呢? 补充题3:X>50 虽然这个不等式明确表示了车速应满足的条件,但我们希望更明确得出x应取哪些值. 与方程类似,我们把使不等式成立的未知数的值叫做不等式的解. 你认为车速可以是60千米/小时吗?可以是75千米/小时吗?可以是80千米/小时吗?你是怎样思考的?
在这里,80是不等式 的解,60和75不是不等式 的解
