人教版八年级上册第十二章全等三角形复习课件(共33张PPT)
文档属性
| 名称 | 人教版八年级上册第十二章全等三角形复习课件(共33张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 538.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-13 22:55:36 | ||
图片预览




文档简介
(共33张PPT)
——复习课
八年级 数学 上册
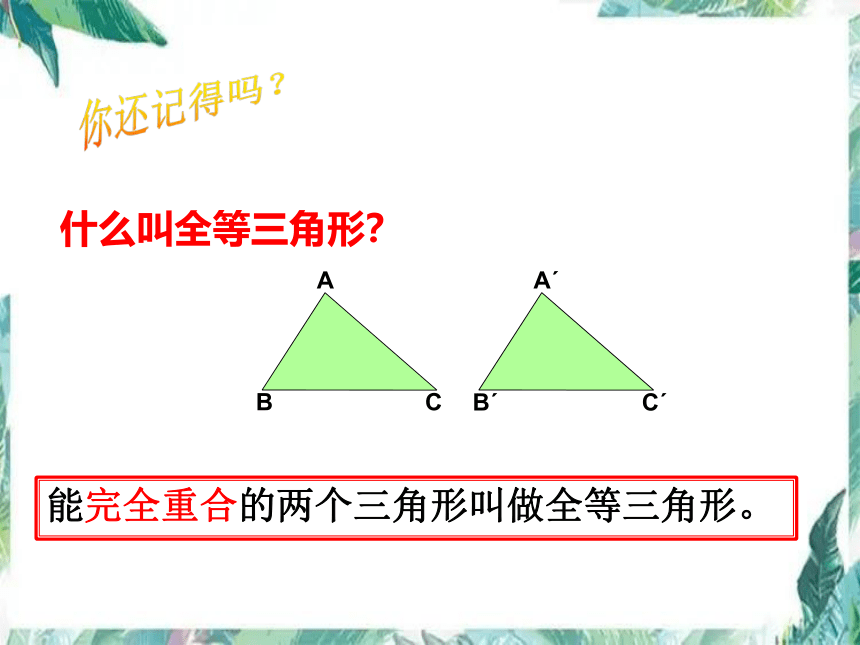
A
B
C
什么叫全等三角形?
能完全重合的两个三角形叫做全等三角形。
你还记得吗?
Aˊ
Bˊ
Cˊ
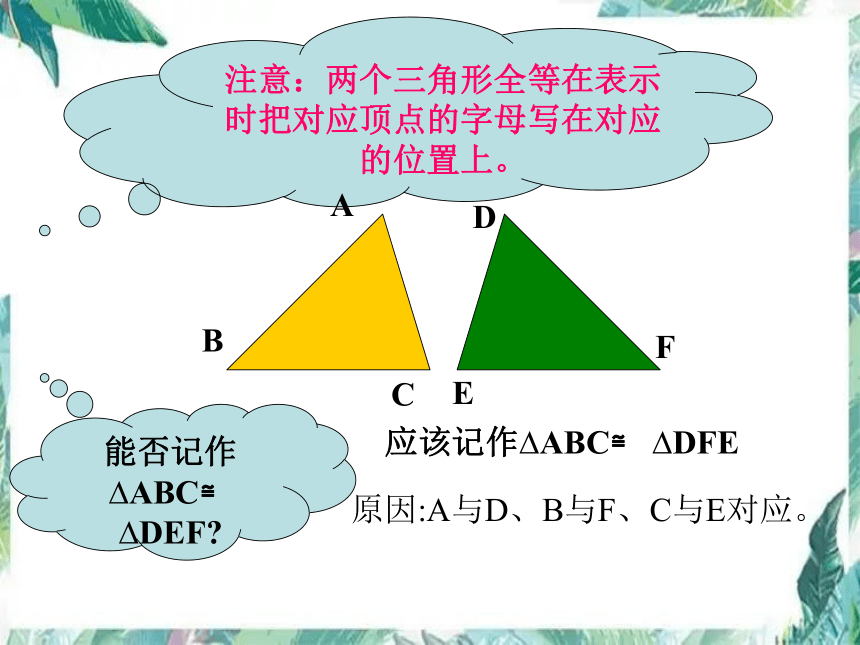
注意:两个三角形全等在表示时把对应顶点的字母写在对应的位置上。
A
C
B
F
E
D
能否记作 ABC≌ DEF
应该记作 ABC≌ DFE
原因:A与D、B与F、C与E对应。
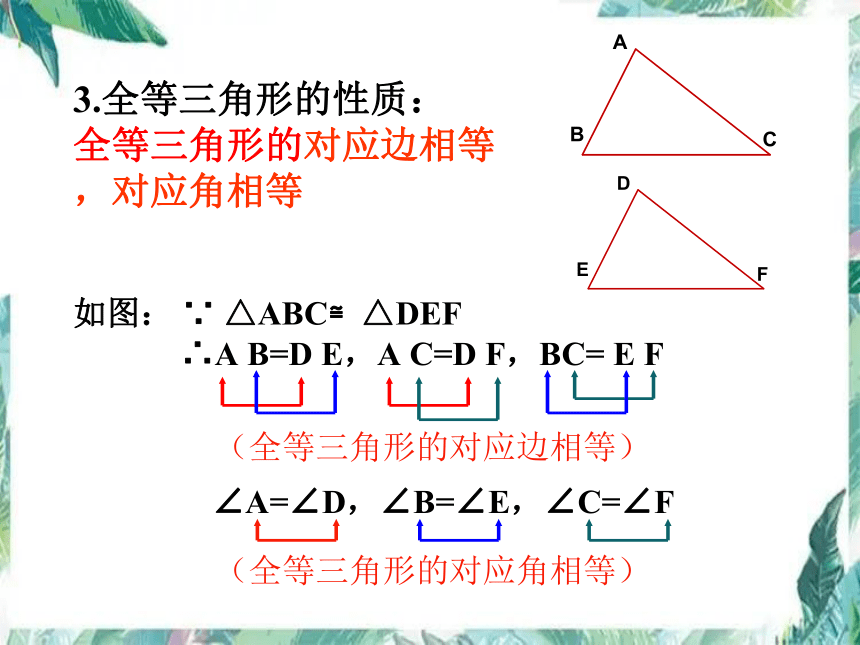
如图: ∵ △ABC≌△DEF
3.全等三角形的性质: 全等三角形的对应边相等,对应角相等
∴A B=D E,A C=D F,BC= E F
∠A=∠D,∠B=∠E,∠C=∠F
(全等三角形的对应边相等)
(全等三角形的对应角相等)
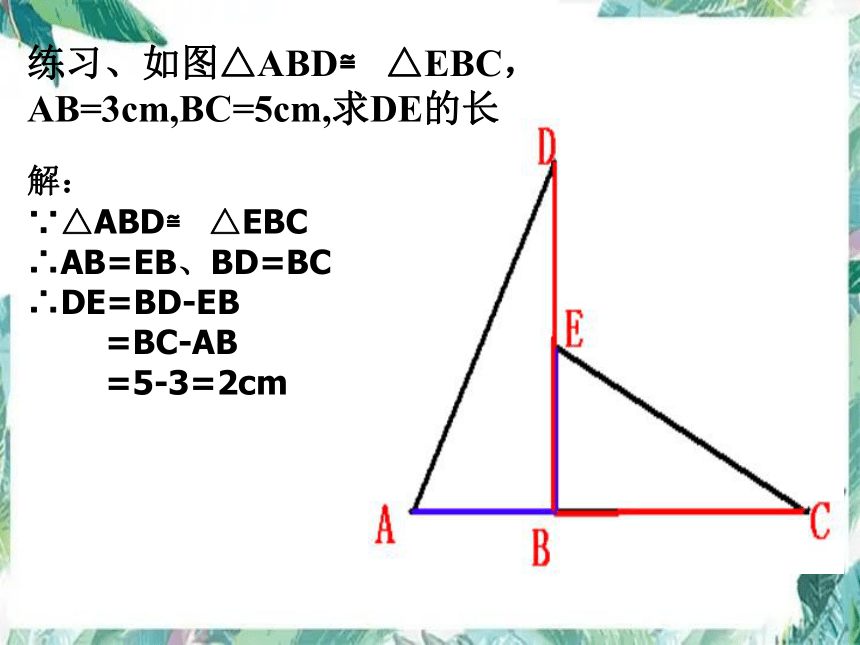
练习、如图△ABD≌ △EBC,AB=3cm,BC=5cm,求DE的长
解:
∵△ABD≌ △EBC
∴AB=EB、BD=BC
∴DE=BD-EB
=BC-AB
=5-3=2cm
边边边 (SSS)
两边一角
两角一边
角角角(AAA)
两边和它的夹角(SAS)
两边和它一边的对角(SSA)
两角和夹边(ASA)
两角和一角的对边(AAS)
三角形全等的判定需要三个条件,
可能出现的情况
两边和其中一边的对角对应相等的两个三角形不一定全等。
\
=
\
=
SSA
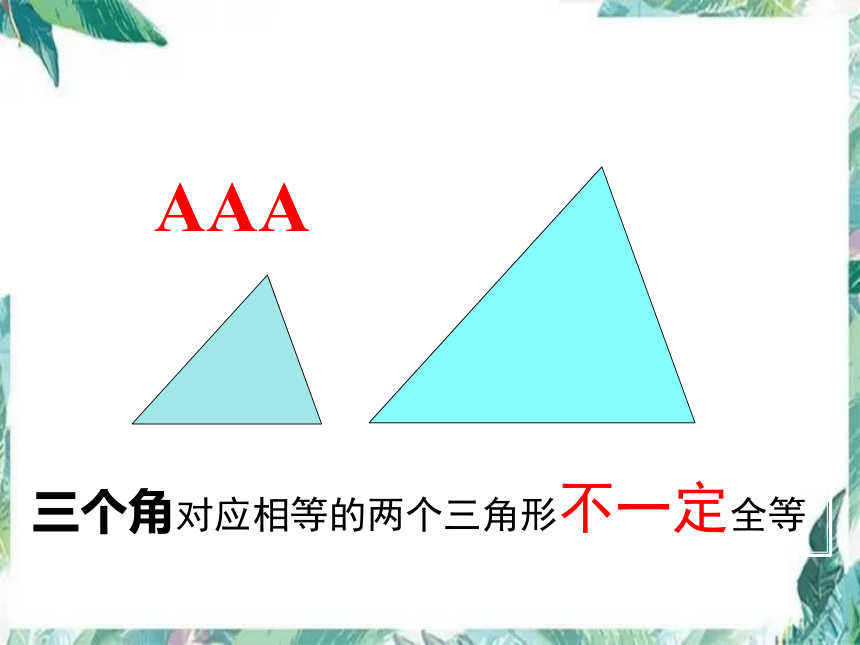
三个角对应相等的两个三角形不一定全等
AAA
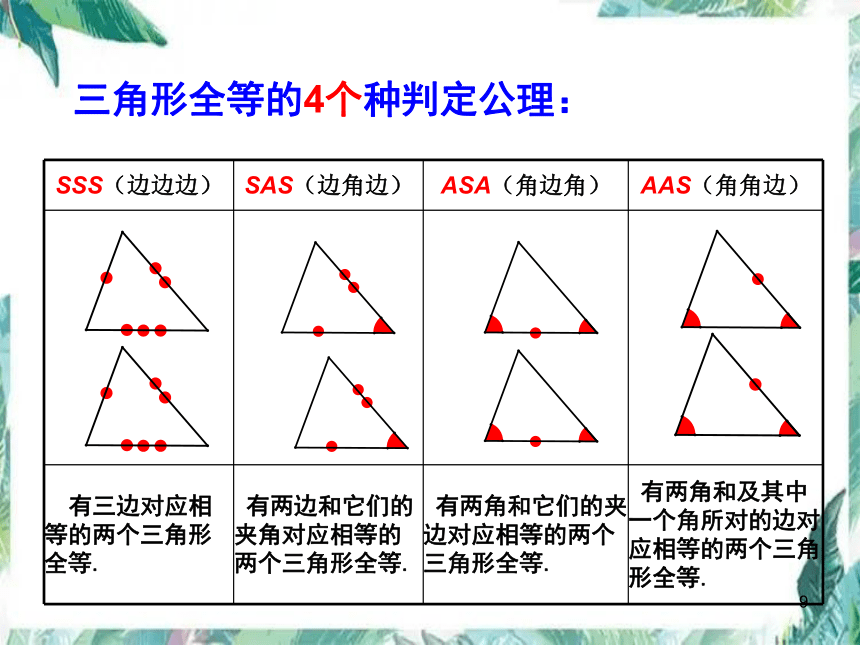
三角形全等的4个种判定公理:SSS(边边边)SAS(边角边)ASA(角边角)AAS(角角边)有三边对应相等的两个三角形全等.有两边和它们的夹角对应相等的两个三角形全等.有两角和它们的夹边对应相等的两个三角形全等.有两角和及其中一个角所对的边对应相等的两个三角形全等.判定三角形全等的思路:
归纳:两个三角形全等,通常需要3个条件,其中至少要有1组 对应相等。
边
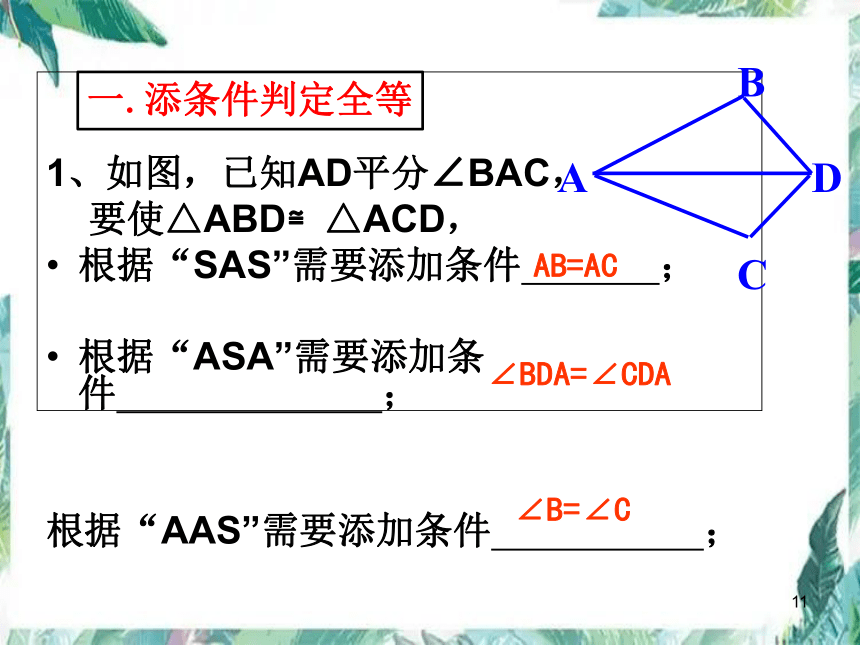
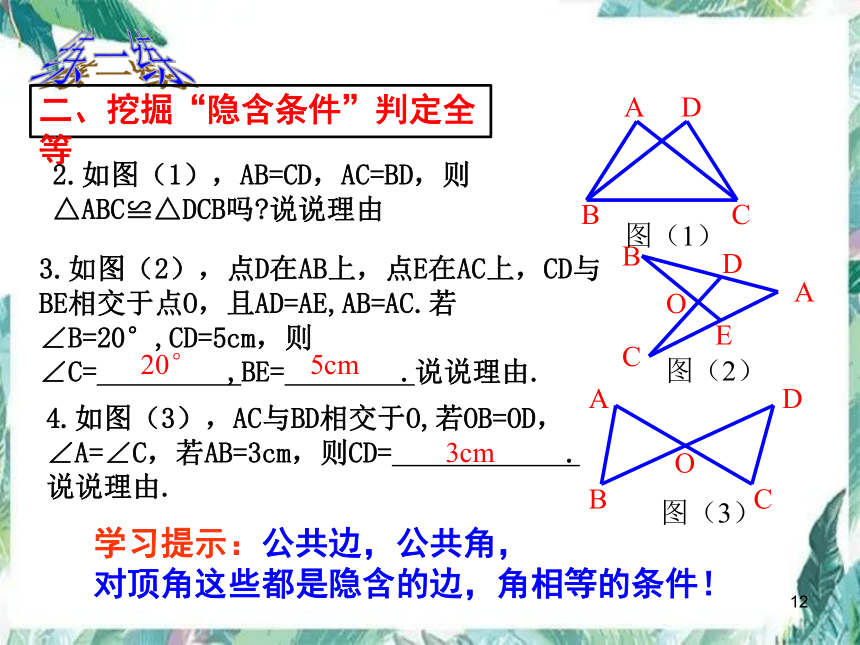
1、如图,已知AD平分∠BAC,要使△ABD≌△ACD,根据“SAS”需要添加条件;根据“ASA”需要添加条件;根据“AAS”需要添加条件;ABCDAB=AC∠BDA=∠CDA∠B=∠C一.添条件判定全等练一练二、挖掘“隐含条件”判定全等2.如图(1),AB=CD,AC=BD,则△ABC≌△DCB吗 说说理由ADBC图(1)3.如图(2),点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC.若∠B=20°,CD=5cm,则∠C=,BE=.说说理由.BCODEA图(2)4.如图(3),AC与BD相交于O,若OB=OD,∠A=∠C,若AB=3cm,则CD=.说说理由.ADBCO图(3)20°5cm3cm学习提示:公共边,公共角,对顶角这些都是隐含的边,角相等的条件!5、已知:∠B=∠DEF,BC=EF,现要证明△ABC≌△DEF,若要以“SAS”为依据,还缺条件______;若要以“ASA”为依据,还缺条件_______;若要以“AAS”为依据,还缺条件_______并说明理由。.AB=DE∠ACB=∠F∠A=∠DABCDEF练习1:如图,AE=AD,要使ΔABD≌ΔACE,请你增加一个条件是 .
练习2:如图,已知∠1=∠2,AC=AD,增加下列件:①AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使ΔABC≌ΔAED的条件有( )个. A.4 B.3 C.2 D.1
2、如图,D在AB上,E在AC上,AB=AC ,∠B=∠C, 试问AD=AE吗?为什么?
E
D
C
B
A
解: AD=AE
理由: 在△ACD和△ABE中
∠B=∠C
AB=AC
∠A=∠A
∴ △ACD≌△ABE (ASA)
∴ AD=AE
例、如图,已知AB=AC,AD=AE,AB、DC相交于点M,AC、BE相交于点N,∠1=∠2,试说明:(1)△ABE ≌ △ACD(2)AM=ANANMEDCB12创造条件! ?总结提高
学习全等三角形应注意以下几个问题:
(1):要正确区分“对应边”与“对边”,“对应角”与 “对角”的不同含义;
(2):表示两个三角形全等时,表示对应顶点的字母要写在对应的位置上;
(3):要记住“有三个角对应相等”或“有两边及其中一边的对角对应相等”的两个三角形不一定全等;
(4):时刻注意图形中的隐含条件,如 “公共角” 、“公共边”、“对顶角”
试一试三、熟练转化“间接条件”判全等1.如图,AE=CF,∠AFD=∠CEB,DF=BE,△AFD与△ CEB全等吗?为什么?ADBCFE3.“三月三,放风筝”如图(6)是小东同学自己做的风筝,他根据AB=AD,BC=DC,不用度量,就知道∠ABC=∠ADC。请用所学的知识给予说明。2.如图(5)∠CAE=∠BAD,∠B=∠D,AC=AE,△ABC与△ADE全等吗?为什么?ACEBD如图(4)AE=CF,∠AFD=∠CEB,DF=BE,△AFD与△ CEB全等吗?为什么?解:∵AE=CF(已知)ADBCFE∴AE-FE=CF-EF(等量减等量,差相等)即AF=CE在△AFD和△CEB中,∴△AFD≌△CEB∠AFD=∠CEB(已知)DF=BE(已知)AF=CE(已证)(SAS)如图(5)∠CAE=∠BAD,∠B=∠D,AC=AE,△ABC与△ADE全等吗?为什么?ACEBD解:∵∠CAE=∠BAD(已知)∴∠CAE+∠BAE=∠BAD+∠BAE(等量减等量,差相等)即∠BAC=∠DAE在△ABC和△ADE中,∴△ABC≌△ADE∠BAC=∠DAE(已证)AC=AE(已知)∠B=∠D(已知)(AAS)“三月三,放风筝”如图(6)是小东同学自己做的风筝,他根据AB=AD,BC=DC,不用度量,就知道∠ABC=∠ADC。请用所学的知识给予说明。解:连接AC∴△ADC≌△ABC(SSS)∴∠ABC=∠ADC(全等三角形的对应角相等)在△ABC和△ADC中,BC=DC(已知)AC=AC(公共边)AB=AD(已知)如图,M是AB的中点,∠1 = 2 ,MC=MD.试说明ΔACM≌ΔBDMABMCD()12解:∵ M是AB的中点(已知)∴ MA=MB(中点定义)在ΔACM和ΔBDM中,MA=MB(已证)∠1 = ∠2 (已知)MC=MD(已知)∴ΔACM ≌ ΔBDM (SAS)如图, M、N分别在AB和AC上, CM与BN相交于点O,若BM = CN, ∠B=∠C .请找出图中所有相等的线段,并说明理由.COBAMN如图,CA=CB,AD=BD,M、N分别是CA、CB的中点,则DM=DN,说明理由。ACDBMN如图,AB=DC,AC=DB, 你能说明图中∠1=∠2的理由吗?ABCD127:已知 AC=DB, ∠1=∠2.
试说明: ∠A=∠D
2
1
D
C
B
A
解:在△ABC和△DCB中
AC=DB
∠1=∠2
BC=CB
∴ △ABC≌△DCB (SAS)
∴ ∠A=∠D
如图,AB∥DC,AD∥BC,说出△ABD≌ △CDB的理由。ABCD如图AB=CD,AD=BC,O为AD中点,过O点的直线分别交AD、BC于M、N,你能说明∠1=∠2吗?12DABCO总结提高
学习全等三角形应注意以下几个问题:
(1):要正确区分“对应边”与“对边”,“对应角”与 “对角”的不同含义;
(2):表示两个三角形全等时,表示对应顶点的字母要写在对应的位置上;
(3):要记住“有三个角对应相等”或“有两边及其中一边的对角对应相等”的两个三角形不一定全等;
(4):时刻注意图形中的隐含条件,如 “公共角” 、“公共边”、“对顶角”
——复习课
八年级 数学 上册
A
B
C
什么叫全等三角形?
能完全重合的两个三角形叫做全等三角形。
你还记得吗?
Aˊ
Bˊ
Cˊ
注意:两个三角形全等在表示时把对应顶点的字母写在对应的位置上。
A
C
B
F
E
D
能否记作 ABC≌ DEF
应该记作 ABC≌ DFE
原因:A与D、B与F、C与E对应。
如图: ∵ △ABC≌△DEF
3.全等三角形的性质: 全等三角形的对应边相等,对应角相等
∴A B=D E,A C=D F,BC= E F
∠A=∠D,∠B=∠E,∠C=∠F
(全等三角形的对应边相等)
(全等三角形的对应角相等)
练习、如图△ABD≌ △EBC,AB=3cm,BC=5cm,求DE的长
解:
∵△ABD≌ △EBC
∴AB=EB、BD=BC
∴DE=BD-EB
=BC-AB
=5-3=2cm
边边边 (SSS)
两边一角
两角一边
角角角(AAA)
两边和它的夹角(SAS)
两边和它一边的对角(SSA)
两角和夹边(ASA)
两角和一角的对边(AAS)
三角形全等的判定需要三个条件,
可能出现的情况
两边和其中一边的对角对应相等的两个三角形不一定全等。
\
=
\
=
SSA
三个角对应相等的两个三角形不一定全等
AAA
三角形全等的4个种判定公理:SSS(边边边)SAS(边角边)ASA(角边角)AAS(角角边)有三边对应相等的两个三角形全等.有两边和它们的夹角对应相等的两个三角形全等.有两角和它们的夹边对应相等的两个三角形全等.有两角和及其中一个角所对的边对应相等的两个三角形全等.判定三角形全等的思路:
归纳:两个三角形全等,通常需要3个条件,其中至少要有1组 对应相等。
边
1、如图,已知AD平分∠BAC,要使△ABD≌△ACD,根据“SAS”需要添加条件;根据“ASA”需要添加条件;根据“AAS”需要添加条件;ABCDAB=AC∠BDA=∠CDA∠B=∠C一.添条件判定全等练一练二、挖掘“隐含条件”判定全等2.如图(1),AB=CD,AC=BD,则△ABC≌△DCB吗 说说理由ADBC图(1)3.如图(2),点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC.若∠B=20°,CD=5cm,则∠C=,BE=.说说理由.BCODEA图(2)4.如图(3),AC与BD相交于O,若OB=OD,∠A=∠C,若AB=3cm,则CD=.说说理由.ADBCO图(3)20°5cm3cm学习提示:公共边,公共角,对顶角这些都是隐含的边,角相等的条件!5、已知:∠B=∠DEF,BC=EF,现要证明△ABC≌△DEF,若要以“SAS”为依据,还缺条件______;若要以“ASA”为依据,还缺条件_______;若要以“AAS”为依据,还缺条件_______并说明理由。.AB=DE∠ACB=∠F∠A=∠DABCDEF练习1:如图,AE=AD,要使ΔABD≌ΔACE,请你增加一个条件是 .
练习2:如图,已知∠1=∠2,AC=AD,增加下列件:①AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使ΔABC≌ΔAED的条件有( )个. A.4 B.3 C.2 D.1
2、如图,D在AB上,E在AC上,AB=AC ,∠B=∠C, 试问AD=AE吗?为什么?
E
D
C
B
A
解: AD=AE
理由: 在△ACD和△ABE中
∠B=∠C
AB=AC
∠A=∠A
∴ △ACD≌△ABE (ASA)
∴ AD=AE
例、如图,已知AB=AC,AD=AE,AB、DC相交于点M,AC、BE相交于点N,∠1=∠2,试说明:(1)△ABE ≌ △ACD(2)AM=ANANMEDCB12创造条件! ?总结提高
学习全等三角形应注意以下几个问题:
(1):要正确区分“对应边”与“对边”,“对应角”与 “对角”的不同含义;
(2):表示两个三角形全等时,表示对应顶点的字母要写在对应的位置上;
(3):要记住“有三个角对应相等”或“有两边及其中一边的对角对应相等”的两个三角形不一定全等;
(4):时刻注意图形中的隐含条件,如 “公共角” 、“公共边”、“对顶角”
试一试三、熟练转化“间接条件”判全等1.如图,AE=CF,∠AFD=∠CEB,DF=BE,△AFD与△ CEB全等吗?为什么?ADBCFE3.“三月三,放风筝”如图(6)是小东同学自己做的风筝,他根据AB=AD,BC=DC,不用度量,就知道∠ABC=∠ADC。请用所学的知识给予说明。2.如图(5)∠CAE=∠BAD,∠B=∠D,AC=AE,△ABC与△ADE全等吗?为什么?ACEBD如图(4)AE=CF,∠AFD=∠CEB,DF=BE,△AFD与△ CEB全等吗?为什么?解:∵AE=CF(已知)ADBCFE∴AE-FE=CF-EF(等量减等量,差相等)即AF=CE在△AFD和△CEB中,∴△AFD≌△CEB∠AFD=∠CEB(已知)DF=BE(已知)AF=CE(已证)(SAS)如图(5)∠CAE=∠BAD,∠B=∠D,AC=AE,△ABC与△ADE全等吗?为什么?ACEBD解:∵∠CAE=∠BAD(已知)∴∠CAE+∠BAE=∠BAD+∠BAE(等量减等量,差相等)即∠BAC=∠DAE在△ABC和△ADE中,∴△ABC≌△ADE∠BAC=∠DAE(已证)AC=AE(已知)∠B=∠D(已知)(AAS)“三月三,放风筝”如图(6)是小东同学自己做的风筝,他根据AB=AD,BC=DC,不用度量,就知道∠ABC=∠ADC。请用所学的知识给予说明。解:连接AC∴△ADC≌△ABC(SSS)∴∠ABC=∠ADC(全等三角形的对应角相等)在△ABC和△ADC中,BC=DC(已知)AC=AC(公共边)AB=AD(已知)如图,M是AB的中点,∠1 = 2 ,MC=MD.试说明ΔACM≌ΔBDMABMCD()12解:∵ M是AB的中点(已知)∴ MA=MB(中点定义)在ΔACM和ΔBDM中,MA=MB(已证)∠1 = ∠2 (已知)MC=MD(已知)∴ΔACM ≌ ΔBDM (SAS)如图, M、N分别在AB和AC上, CM与BN相交于点O,若BM = CN, ∠B=∠C .请找出图中所有相等的线段,并说明理由.COBAMN如图,CA=CB,AD=BD,M、N分别是CA、CB的中点,则DM=DN,说明理由。ACDBMN如图,AB=DC,AC=DB, 你能说明图中∠1=∠2的理由吗?ABCD127:已知 AC=DB, ∠1=∠2.
试说明: ∠A=∠D
2
1
D
C
B
A
解:在△ABC和△DCB中
AC=DB
∠1=∠2
BC=CB
∴ △ABC≌△DCB (SAS)
∴ ∠A=∠D
如图,AB∥DC,AD∥BC,说出△ABD≌ △CDB的理由。ABCD如图AB=CD,AD=BC,O为AD中点,过O点的直线分别交AD、BC于M、N,你能说明∠1=∠2吗?12DABCO总结提高
学习全等三角形应注意以下几个问题:
(1):要正确区分“对应边”与“对边”,“对应角”与 “对角”的不同含义;
(2):表示两个三角形全等时,表示对应顶点的字母要写在对应的位置上;
(3):要记住“有三个角对应相等”或“有两边及其中一边的对角对应相等”的两个三角形不一定全等;
(4):时刻注意图形中的隐含条件,如 “公共角” 、“公共边”、“对顶角”
