人教版八年级上册第十二章全等三角形复习课课件(共21张PPT)
文档属性
| 名称 | 人教版八年级上册第十二章全等三角形复习课课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 351.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-13 22:57:44 | ||
图片预览



文档简介
(共21张PPT)
全等三角形的复习
你知道吗?
1、什么是全等图形?把一个图形进行平移、
旋转、翻折后所得图形与原图形全等.
2、什么是全等三角形?
3、全等三角形的性质?
4、三角形全等有哪几种判定方法?
5、如何用尺规画角平分线?一个角的角平分
线有哪些性质、判定?
全等三角形的性质:
全等三角形的对应边、对应角相等.
全等三角形的判定
知识点回顾
SAS、ASA、AAS、SSS、HL
全等图形的定义:
能完全重合的图形叫全等图形.
全等三角形的定义:
能完全重合的三角形是全等三角形.
角平分线的性质、判定:
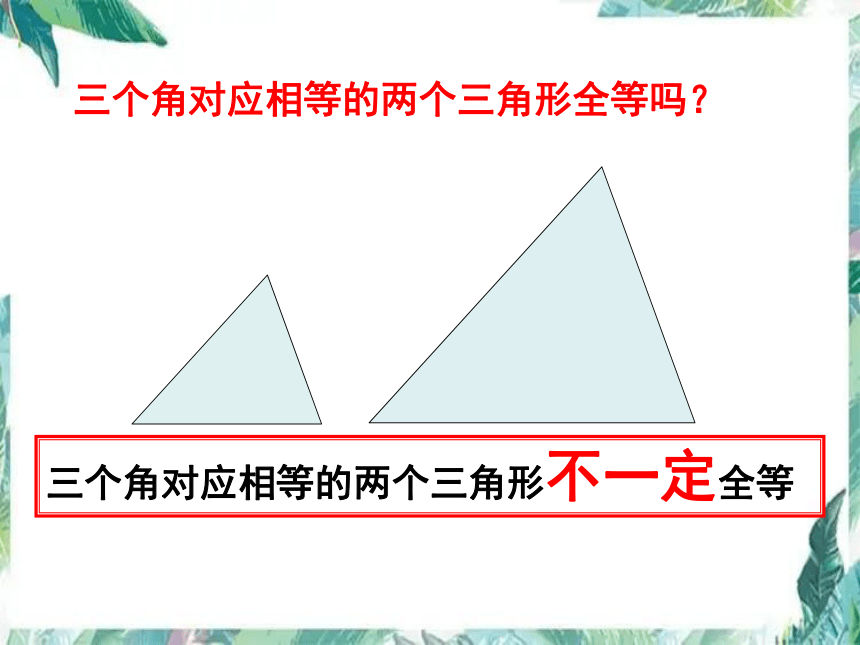
三个角对应相等的两个三角形不一定全等
三个角对应相等的两个三角形全等吗?
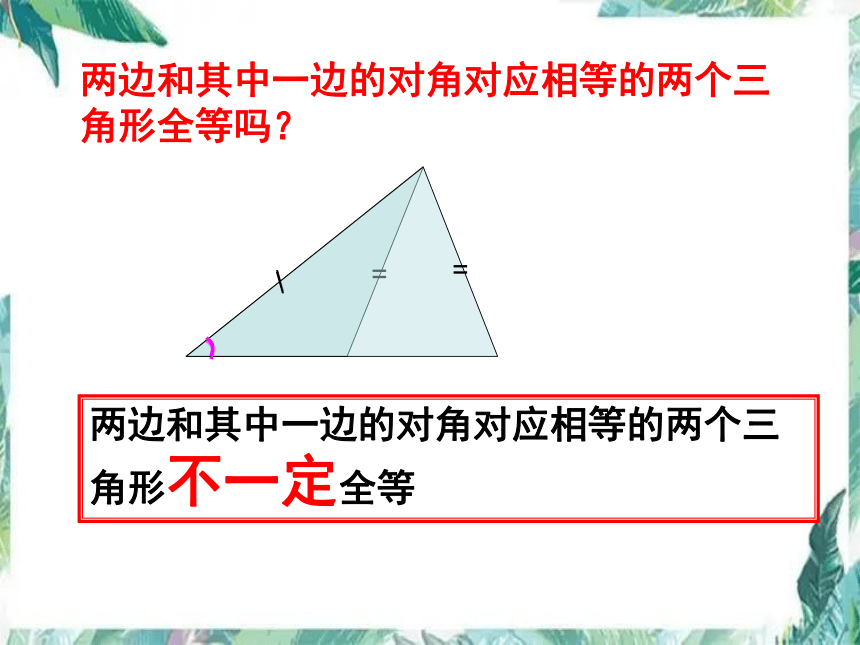
两边和其中一边的对角对应相等的两个三角形不一定全等
两边和其中一边的对角对应相等的两个三角形全等吗?
\
=
\
=
练一练
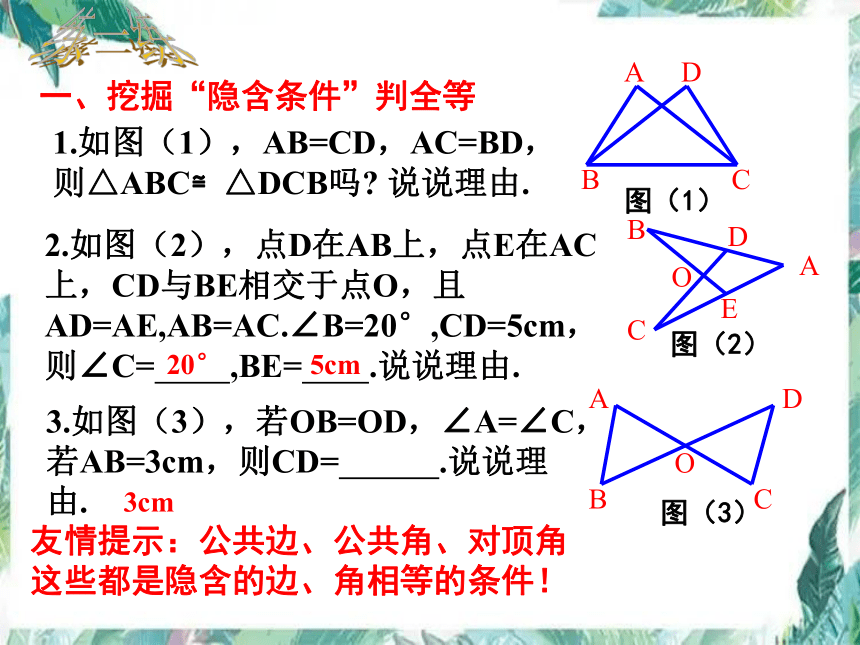
一、挖掘“隐含条件”判全等
1.如图(1),AB=CD,AC=BD,则△ABC≌△DCB吗 说说理由.
A
D
B
C
图(1)
2.如图(2),点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC.∠B=20°,CD=5cm,则∠C= ,BE= .说说理由.
B
C
O
D
E
A
图(2)
3.如图(3),若OB=OD,∠A=∠C,若AB=3cm,则CD= .说说理由.
A
D
B
C
O
图(3)
20°
5cm
3cm
友情提示:公共边、公共角、对顶角
这些都是隐含的边、角相等的条件!
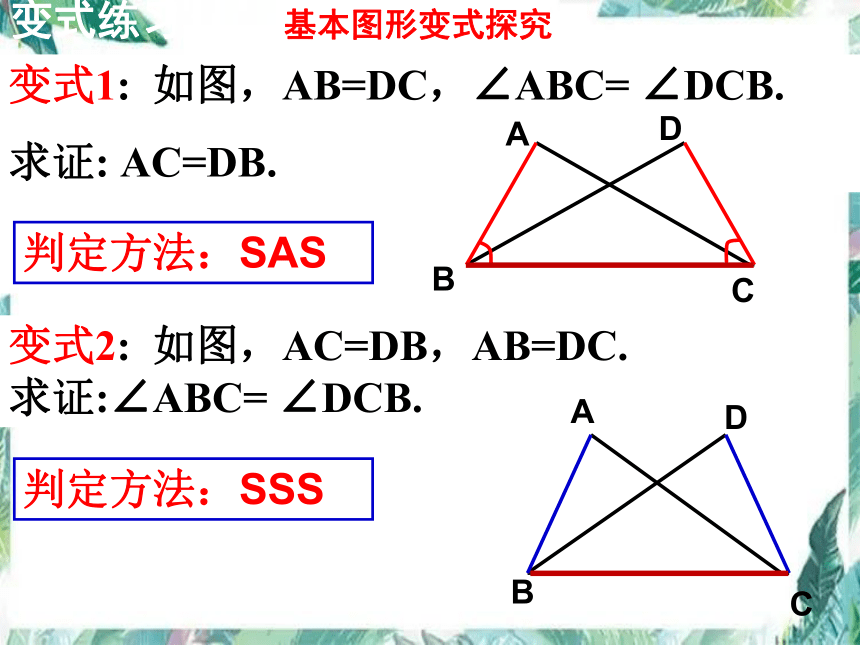
变式1: 如图,AB=DC,∠ABC= ∠DCB.
求证: AC=DB.
B
C
A
D
基本图形变式探究
变式练习:
变式2: 如图,AC=DB,AB=DC.
求证:∠ABC= ∠DCB.
B
C
A
D
判定方法:SAS
判定方法:SSS
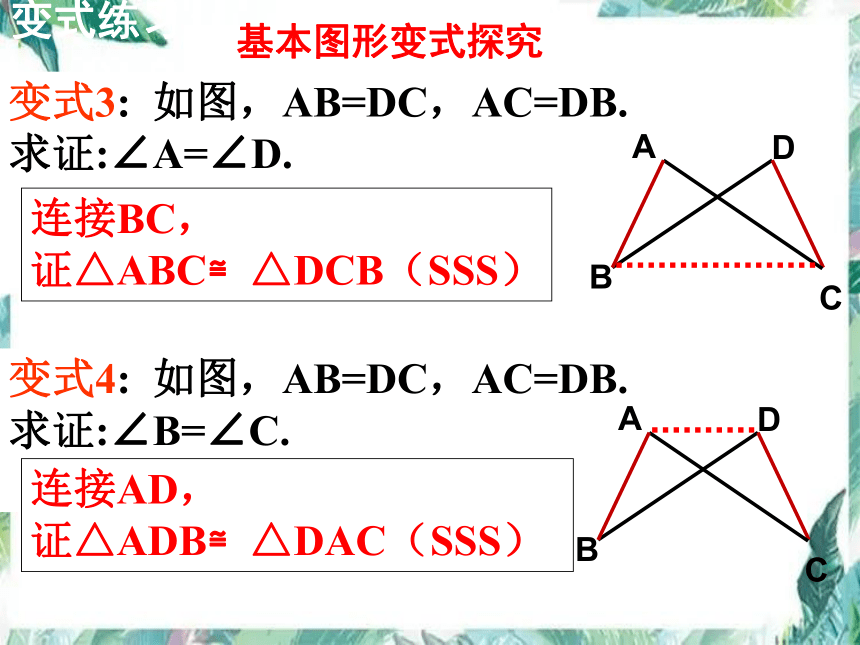
变式3: 如图,AB=DC,AC=DB.
求证:∠A=∠D.
B
C
A
D
变式练习:
基本图形变式探究
变式4: 如图,AB=DC,AC=DB.
求证:∠B=∠C.
B
C
A
D
连接BC,
证△ABC≌△DCB(SSS)
连接AD,
证△ADB≌△DAC(SSS)
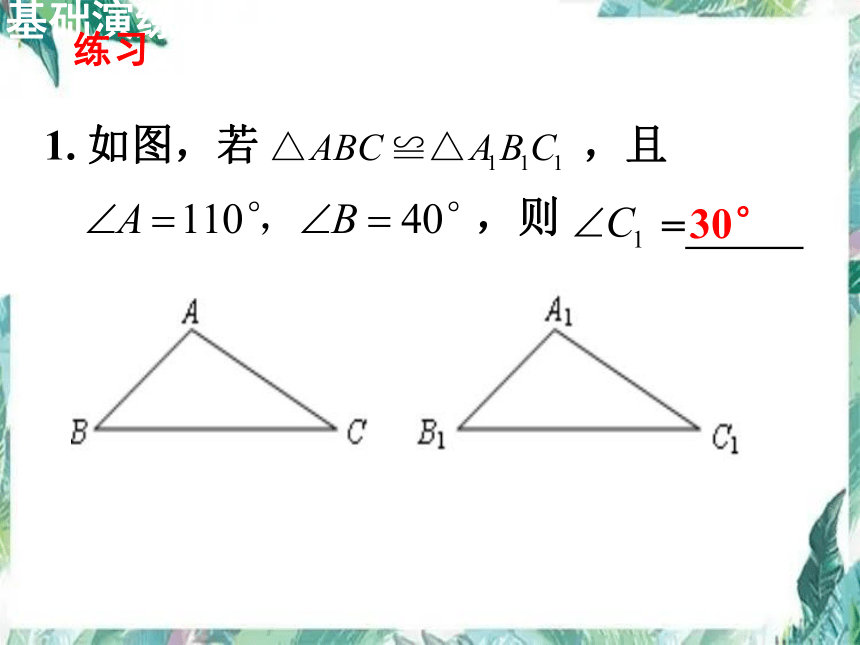
1. 如图,若
,且
,则
=
基础演练:
30°
练习
2. 如图,已知AD平分∠BAC,
要使△ABD≌△ACD,
根据“SAS”需要添加条件 ;
根据“ASA”需要添加条件 ;
根据“AAS”需要添加条件 ;
A
B
C
D
AB=AC
∠BDA=∠CDA
∠B=∠C
友情提示:添加条件的题目,首先要找到已具备的条件,这些条件有些是题目已知条件,有些是图中隐含条件.
添加条件判定全等
3. 已知,如图,下列条件中,能证明△ABC≌△DEF的有哪些?请说明理由.
(1)△ABC和△DEF能够完全重合;
(2)AB=DE;AC=DF;BC=EF;
(3) AB=DE;AC=DF; ∠ B= ∠ E
(4) ∠ A= ∠ D; ∠ B= ∠ E;AB=DE
基础演练:
A
B
C
D
E
F
定义
SSS
ASA
(1)(2)(4)
4. 在下列说法中,正确的有( )个.并说明判断的理由.
①三角对应相等的两个三角形全等
②三边对应相等的两个三角形全等
③两角、一边对应相等的两个三角形全等
④两边、一角对应相等的两个三角形全等
A.1 B.2 C.3 D.4
基础演练:
5.如图,将两根钢条AA'、BB'的中点O连在一起,使AA'、BB'可以绕着点O自由转动,就做成了一个测量工件,则A'B'的长等于内槽宽AB,那么判定△OAB≌△OA 'B '的理由是( )
A.边角边; B.角边角;
C.边边边; D.角角边 .
基础演练:
例1: 如图,点B在AE上,∠CAB=∠DAB,要使ΔABC≌ΔABD,可补充的一个条件是 .
分析:已有的条件
SAS
ASA
AAS
S→ AB=AB(公共边) .
自主探究:
条件开放题型探究
A→∠CAB=∠DAB
练习:如图,已知∠B=∠DEF,AB=DE,要说明△ABC≌△DEF,
(1)若以“SAS”为依据,还须添加的一个条件为 ;
(2)若以“ASA”为依据,还须添加的一个条件为 ;
(3)若以“AAS”为依据,还须添加的一个条件为 .
BC=EF
∠A=∠D
∠ACB=∠F
条件开放题型探究
或BE=CF
例2 已知:如图,AC平分∠BAD,
CE⊥AB于E,CF⊥AD于F,且BC=DC.
你能说明BE与DF相等吗?
A
B
C
D
E
F
1
2
书写证明过程题
例3:已知如图,AB⊥DC于B,且BD=BA,
BE=BC.
问:AC与DE有什么关系呢?
典例分析:
基本图形变式探究
F
变式1.将上题中的△DBE沿DC方向平移
变式练习:
A
B
C
E
D
E
D
F
基本图形变式探究
变式2. 将上题中的△DBE沿DC方向平移
变式练习:
A
B
C
E
D
F
E
D
F
基本图形变式探究
变式3. 将上题中的△DBE沿DC方向平移,得到下列图形。
变式练习:
基本图形变式探究
下列情况中,DE=AC、DE⊥AC吗?为什么?
已知:AB⊥DC,EF⊥DC,AB=DF,BC=FE
1. 全等三角形的定义,性质,
判定方法.
2. 证明题的方法①要证什么
②已有什么
③还缺什么
④创造条件
3. 添加辅助线
小结:
全等三角形的复习
你知道吗?
1、什么是全等图形?把一个图形进行平移、
旋转、翻折后所得图形与原图形全等.
2、什么是全等三角形?
3、全等三角形的性质?
4、三角形全等有哪几种判定方法?
5、如何用尺规画角平分线?一个角的角平分
线有哪些性质、判定?
全等三角形的性质:
全等三角形的对应边、对应角相等.
全等三角形的判定
知识点回顾
SAS、ASA、AAS、SSS、HL
全等图形的定义:
能完全重合的图形叫全等图形.
全等三角形的定义:
能完全重合的三角形是全等三角形.
角平分线的性质、判定:
三个角对应相等的两个三角形不一定全等
三个角对应相等的两个三角形全等吗?
两边和其中一边的对角对应相等的两个三角形不一定全等
两边和其中一边的对角对应相等的两个三角形全等吗?
\
=
\
=
练一练
一、挖掘“隐含条件”判全等
1.如图(1),AB=CD,AC=BD,则△ABC≌△DCB吗 说说理由.
A
D
B
C
图(1)
2.如图(2),点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC.∠B=20°,CD=5cm,则∠C= ,BE= .说说理由.
B
C
O
D
E
A
图(2)
3.如图(3),若OB=OD,∠A=∠C,若AB=3cm,则CD= .说说理由.
A
D
B
C
O
图(3)
20°
5cm
3cm
友情提示:公共边、公共角、对顶角
这些都是隐含的边、角相等的条件!
变式1: 如图,AB=DC,∠ABC= ∠DCB.
求证: AC=DB.
B
C
A
D
基本图形变式探究
变式练习:
变式2: 如图,AC=DB,AB=DC.
求证:∠ABC= ∠DCB.
B
C
A
D
判定方法:SAS
判定方法:SSS
变式3: 如图,AB=DC,AC=DB.
求证:∠A=∠D.
B
C
A
D
变式练习:
基本图形变式探究
变式4: 如图,AB=DC,AC=DB.
求证:∠B=∠C.
B
C
A
D
连接BC,
证△ABC≌△DCB(SSS)
连接AD,
证△ADB≌△DAC(SSS)
1. 如图,若
,且
,则
=
基础演练:
30°
练习
2. 如图,已知AD平分∠BAC,
要使△ABD≌△ACD,
根据“SAS”需要添加条件 ;
根据“ASA”需要添加条件 ;
根据“AAS”需要添加条件 ;
A
B
C
D
AB=AC
∠BDA=∠CDA
∠B=∠C
友情提示:添加条件的题目,首先要找到已具备的条件,这些条件有些是题目已知条件,有些是图中隐含条件.
添加条件判定全等
3. 已知,如图,下列条件中,能证明△ABC≌△DEF的有哪些?请说明理由.
(1)△ABC和△DEF能够完全重合;
(2)AB=DE;AC=DF;BC=EF;
(3) AB=DE;AC=DF; ∠ B= ∠ E
(4) ∠ A= ∠ D; ∠ B= ∠ E;AB=DE
基础演练:
A
B
C
D
E
F
定义
SSS
ASA
(1)(2)(4)
4. 在下列说法中,正确的有( )个.并说明判断的理由.
①三角对应相等的两个三角形全等
②三边对应相等的两个三角形全等
③两角、一边对应相等的两个三角形全等
④两边、一角对应相等的两个三角形全等
A.1 B.2 C.3 D.4
基础演练:
5.如图,将两根钢条AA'、BB'的中点O连在一起,使AA'、BB'可以绕着点O自由转动,就做成了一个测量工件,则A'B'的长等于内槽宽AB,那么判定△OAB≌△OA 'B '的理由是( )
A.边角边; B.角边角;
C.边边边; D.角角边 .
基础演练:
例1: 如图,点B在AE上,∠CAB=∠DAB,要使ΔABC≌ΔABD,可补充的一个条件是 .
分析:已有的条件
SAS
ASA
AAS
S→ AB=AB(公共边) .
自主探究:
条件开放题型探究
A→∠CAB=∠DAB
练习:如图,已知∠B=∠DEF,AB=DE,要说明△ABC≌△DEF,
(1)若以“SAS”为依据,还须添加的一个条件为 ;
(2)若以“ASA”为依据,还须添加的一个条件为 ;
(3)若以“AAS”为依据,还须添加的一个条件为 .
BC=EF
∠A=∠D
∠ACB=∠F
条件开放题型探究
或BE=CF
例2 已知:如图,AC平分∠BAD,
CE⊥AB于E,CF⊥AD于F,且BC=DC.
你能说明BE与DF相等吗?
A
B
C
D
E
F
1
2
书写证明过程题
例3:已知如图,AB⊥DC于B,且BD=BA,
BE=BC.
问:AC与DE有什么关系呢?
典例分析:
基本图形变式探究
F
变式1.将上题中的△DBE沿DC方向平移
变式练习:
A
B
C
E
D
E
D
F
基本图形变式探究
变式2. 将上题中的△DBE沿DC方向平移
变式练习:
A
B
C
E
D
F
E
D
F
基本图形变式探究
变式3. 将上题中的△DBE沿DC方向平移,得到下列图形。
变式练习:
基本图形变式探究
下列情况中,DE=AC、DE⊥AC吗?为什么?
已知:AB⊥DC,EF⊥DC,AB=DF,BC=FE
1. 全等三角形的定义,性质,
判定方法.
2. 证明题的方法①要证什么
②已有什么
③还缺什么
④创造条件
3. 添加辅助线
小结:
