人教版八年级上册 第十二章三角形全等的判定复习课件(共15张PPT)
文档属性
| 名称 | 人教版八年级上册 第十二章三角形全等的判定复习课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 148.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-13 23:03:54 | ||
图片预览





文档简介
(共15张PPT)
三角形全等的判定
复习课
知识回顾:
一般三角形 全等的条件:
1.定义(重合)法;
2.SSS;
3.SAS;
4.ASA;
5.AAS.
直角三角形 全等特有的条件:
HL.
包括直角三角形
不包括其它形状的三角形
解题中常用的4种方法
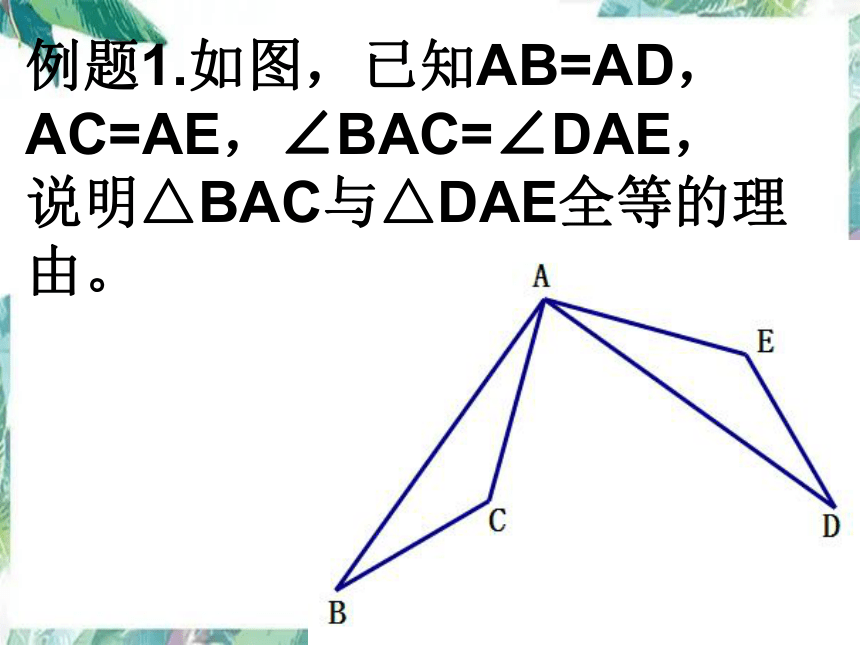
例题1.如图,已知AB=AD,AC=AE,∠BAC=∠DAE,
说明△BAC与△DAE全等的理由。
解:
在△ BAC与△ DAE中,
AB=AD(已知)
∠BAC=∠DAE(已知)
AC=AE(已知)
∴△ BAC≌△ DAE(SAS)
分析:本题利用边角边公理证明两个三角形全等.由题目已知只要证明AF=CE,∠A=∠C
例2 如图2,AE=CF,AD∥BC,AD=CB,
求证:
说明:本题的解题关键是证明AF=CE,∠A=∠ C,易错点是将AE与CF直接作为对应边,而错误地写为:
分析:已知△ABC≌△ A1B1C1 ,相当于已知它们的对应边相等.在证明过程中,可根据需要,选取其中一部分相等关系.
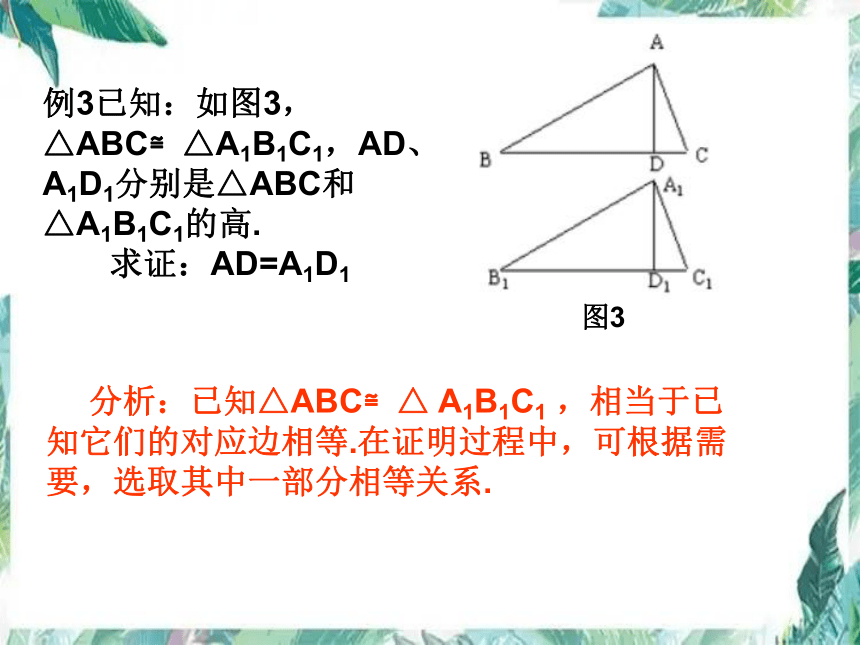
例3已知:如图3,△ABC≌△A1B1C1,AD、A1D1分别是△ABC和△A1B1C1的高.
求证:AD=A1D1
图3
证明:∵△ABC≌△A1B1C1(已知)
∴AB=A1B1,∠B=∠B1(全等三角形的对应边、对应角相等)
∵AD、A1D1分别是△ABC、△A1B1C1的高(已知)
∴∠ADB=∠A1D1B1= 90°.
在△ABC和△A1B1C1中
∠B=∠B1(已证)
∠ADB=∠A1D1B1(已证)
AB=A1B(已证)
∴△ABC≌△A1B1C(AAS)
∴AD=A1D1(全等三角形的对应边相等)
说明:本题为例2的一个延伸题目,关键是利用三角形全等的性质及判定找到相等关系.类似的题目还有角平分线相等、中线相等.
例4:求证:有一条直角边和斜边上的高对应相等的两个直角三角形全等。
分析:首先要分清题设和结论,然后按要求画出图形,根据题意写出、已知求证后,再写出证明过程。
已知: 如图,在Rt△ABC、Rt△ 中,∠ACB=∠ =Rt∠,BC= ,
CD⊥AB于D, ⊥ 于 ,CD=
求证:Rt△ABC≌Rt△
证明:在Rt△CDB和
Rt△ 中
∴Rt△CDB≌Rt△ (HL)
由此得∠B=∠
在△ABC与△ 中
∴△ABC≌△ (ASA)
说明:文字证明题的书写格式要标准。
1.如图1:△ABF≌ △CDE,∠B=30°, ∠BAE= ∠DCF=20 °.求∠EFC的度数.
练习题:
2 、如图2,已知:AD平分∠BAC,AB=AC,连接BD,CD,并延长相交AC、AB于F、E点.则图形中有( )对全等三角形.
A、2 B、3 C4 D、5
C
图1
图2
3、如图3,已知:△ABC中,DF=FE,BD=CE,AF⊥BC于F,则此图中全等三角形共有( )
A、5对 B、4对 C、3对 D2对
4、如图4,已知:在△ABC中,AD是BC边上的高,AD=BD,DE=DC,延长BE交AC于F,
求证:BF是△ABC中边上的高.
提示:关键证明△ADC≌△BFC
B
5、如图5,已知:AB=CD,AD=CB,O为AC任一点,过O作直线分别交AB、CD的延长线于F、E,求证:∠E=∠F.
提示:由条件易证△ABC≌△CDA 从而得知∠BAC=∠DCA ,即:AB∥CD.
6、如图6,已知:∠A=90°, AB=BD,ED⊥BC于 D.
求证:AE=ED
提示:找两个全等三角形,需连结BE.
图6
7、已知如图,AB∥DE,AB=DE,BE=CF
说明
(3)AC∥DF
(1)BC=EF
(2)△ABC≌△DEF
再见
三角形全等的判定
复习课
知识回顾:
一般三角形 全等的条件:
1.定义(重合)法;
2.SSS;
3.SAS;
4.ASA;
5.AAS.
直角三角形 全等特有的条件:
HL.
包括直角三角形
不包括其它形状的三角形
解题中常用的4种方法
例题1.如图,已知AB=AD,AC=AE,∠BAC=∠DAE,
说明△BAC与△DAE全等的理由。
解:
在△ BAC与△ DAE中,
AB=AD(已知)
∠BAC=∠DAE(已知)
AC=AE(已知)
∴△ BAC≌△ DAE(SAS)
分析:本题利用边角边公理证明两个三角形全等.由题目已知只要证明AF=CE,∠A=∠C
例2 如图2,AE=CF,AD∥BC,AD=CB,
求证:
说明:本题的解题关键是证明AF=CE,∠A=∠ C,易错点是将AE与CF直接作为对应边,而错误地写为:
分析:已知△ABC≌△ A1B1C1 ,相当于已知它们的对应边相等.在证明过程中,可根据需要,选取其中一部分相等关系.
例3已知:如图3,△ABC≌△A1B1C1,AD、A1D1分别是△ABC和△A1B1C1的高.
求证:AD=A1D1
图3
证明:∵△ABC≌△A1B1C1(已知)
∴AB=A1B1,∠B=∠B1(全等三角形的对应边、对应角相等)
∵AD、A1D1分别是△ABC、△A1B1C1的高(已知)
∴∠ADB=∠A1D1B1= 90°.
在△ABC和△A1B1C1中
∠B=∠B1(已证)
∠ADB=∠A1D1B1(已证)
AB=A1B(已证)
∴△ABC≌△A1B1C(AAS)
∴AD=A1D1(全等三角形的对应边相等)
说明:本题为例2的一个延伸题目,关键是利用三角形全等的性质及判定找到相等关系.类似的题目还有角平分线相等、中线相等.
例4:求证:有一条直角边和斜边上的高对应相等的两个直角三角形全等。
分析:首先要分清题设和结论,然后按要求画出图形,根据题意写出、已知求证后,再写出证明过程。
已知: 如图,在Rt△ABC、Rt△ 中,∠ACB=∠ =Rt∠,BC= ,
CD⊥AB于D, ⊥ 于 ,CD=
求证:Rt△ABC≌Rt△
证明:在Rt△CDB和
Rt△ 中
∴Rt△CDB≌Rt△ (HL)
由此得∠B=∠
在△ABC与△ 中
∴△ABC≌△ (ASA)
说明:文字证明题的书写格式要标准。
1.如图1:△ABF≌ △CDE,∠B=30°, ∠BAE= ∠DCF=20 °.求∠EFC的度数.
练习题:
2 、如图2,已知:AD平分∠BAC,AB=AC,连接BD,CD,并延长相交AC、AB于F、E点.则图形中有( )对全等三角形.
A、2 B、3 C4 D、5
C
图1
图2
3、如图3,已知:△ABC中,DF=FE,BD=CE,AF⊥BC于F,则此图中全等三角形共有( )
A、5对 B、4对 C、3对 D2对
4、如图4,已知:在△ABC中,AD是BC边上的高,AD=BD,DE=DC,延长BE交AC于F,
求证:BF是△ABC中边上的高.
提示:关键证明△ADC≌△BFC
B
5、如图5,已知:AB=CD,AD=CB,O为AC任一点,过O作直线分别交AB、CD的延长线于F、E,求证:∠E=∠F.
提示:由条件易证△ABC≌△CDA 从而得知∠BAC=∠DCA ,即:AB∥CD.
6、如图6,已知:∠A=90°, AB=BD,ED⊥BC于 D.
求证:AE=ED
提示:找两个全等三角形,需连结BE.
图6
7、已知如图,AB∥DE,AB=DE,BE=CF
说明
(3)AC∥DF
(1)BC=EF
(2)△ABC≌△DEF
再见
