人教版八年级数学上册 第十一章 三角形 复习课课件(共23张PPT)
文档属性
| 名称 | 人教版八年级数学上册 第十一章 三角形 复习课课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 394.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-14 08:27:12 | ||
图片预览




文档简介
(共23张PPT)
第十一章 三角形 (复习课)
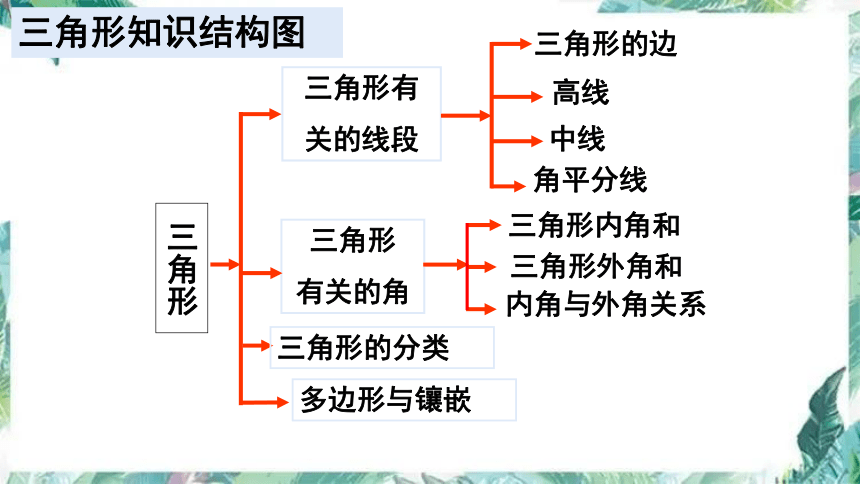
三角形
三角形有
关的线段
三角形内角和
三角形外角和
三角形知识结构图
三角形的边
高线
中线
角平分线
三角形
有关的角
内角与外角关系
三角形的分类
多边形与镶嵌
1. 三角形的三边关系:
(1) 三角形两边的和大于第三边
2. 判断三条已知线段a、b、c能否组成三角形.
较短两边之和大于第三边
3. 确定三角形第三边的取值范围:
两边之差<第三边<两边之和.
(2) 三角形两边的差小于第三边
考点1.与三角形有关的线段
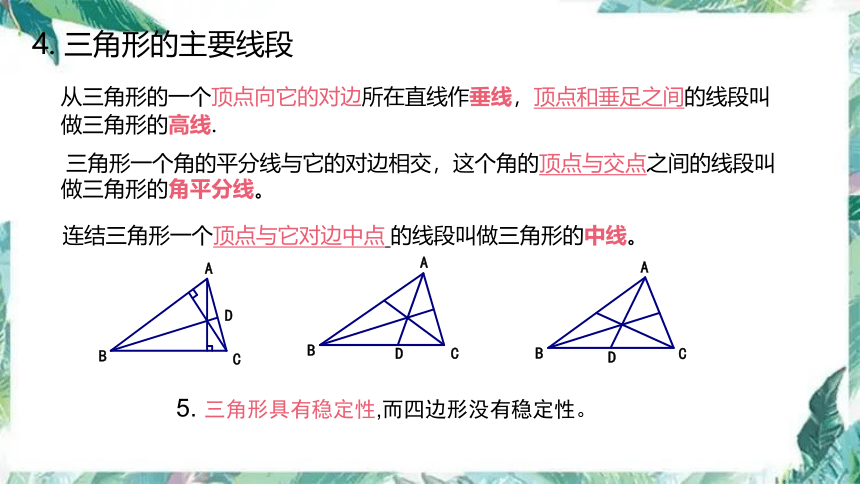
连结三角形一个顶点与它对边中点 的线段叫做三角形的中线。
三角形一个角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线。
从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高线.
4. 三角形的主要线段
5. 三角形具有稳定性,而四边形没有稳定性。
常见考点
1.在下列长度的三条线段中,不能组成三角形的是( )A. 2cm ,3cm ,4 cm B. 3cm ,6cm,7cm
C. 2cm,2cm,6cm D. 5cm,6cm,7cm.
2. 已知三角形两边长分别为1,5,第三边长为整数,则第三边的长为_________。
C
5
3.下列说法中,正确的是( )A. 三角形的角平线是射线
B. 三角形的高总在三角形的内部
C.三角形的高、中线、角平分线一定是三条不同的线段
D.三角形的中线在三角形的内部
D
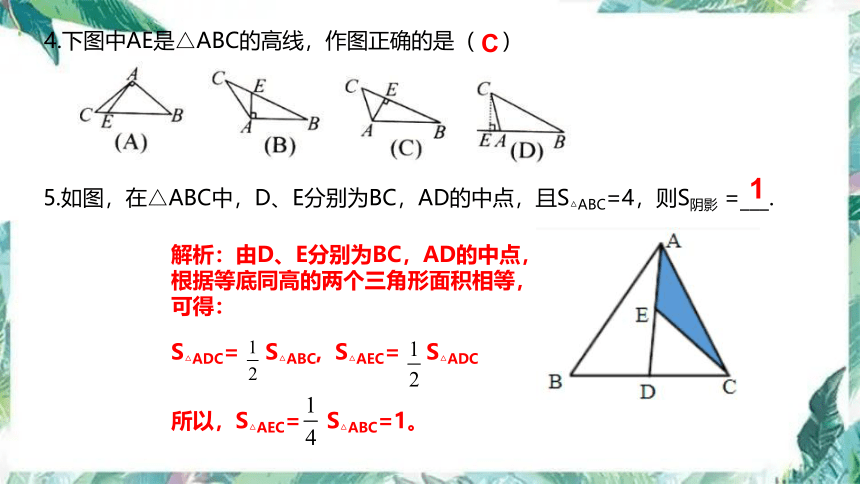
4.下图中AE是△ABC的高线,作图正确的是( )
C
5.如图,在△ABC中,D、E分别为BC,AD的中点,且S△ABC=4,则S阴影 =___.
1
解析:由D、E分别为BC,AD的中点,根据等底同高的两个三角形面积相等,可得:
S△ADC= S△ABC, S△AEC= S△ADC
所以,S△AEC= S△ABC=1。
6. 已知等腰三角形的一边等于8cm,一边等于6cm,则三角形的周长为______________
解析:此题分为两种情况(1)以8cm为腰,6cm为底,则三角形的周长=2×8+6=22(cm)(2)以6cm为腰,8cm为底,则三角形的周长=2×6+8=20(cm)故三角形的周长为22cm或20cm
7.木工师傅在做完门框后,为防止变形,常常像如图所示那样钉上两条斜拉的木板条(即图中的AB、CD两根木条),这样做的数学道理是_____________。
22cm或20cm
三角形的稳定性
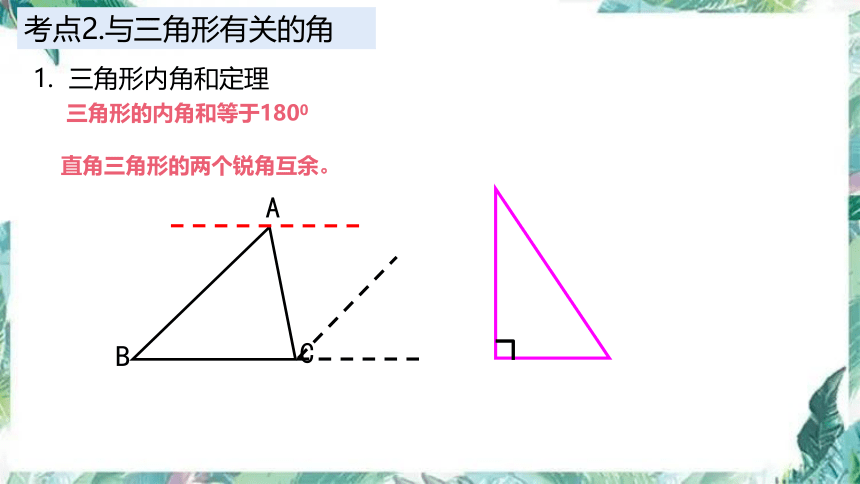
1. 三角形内角和定理
三角形的内角和等于1800
直角三角形的两个锐角互余。
A
B
C
考点2.与三角形有关的角
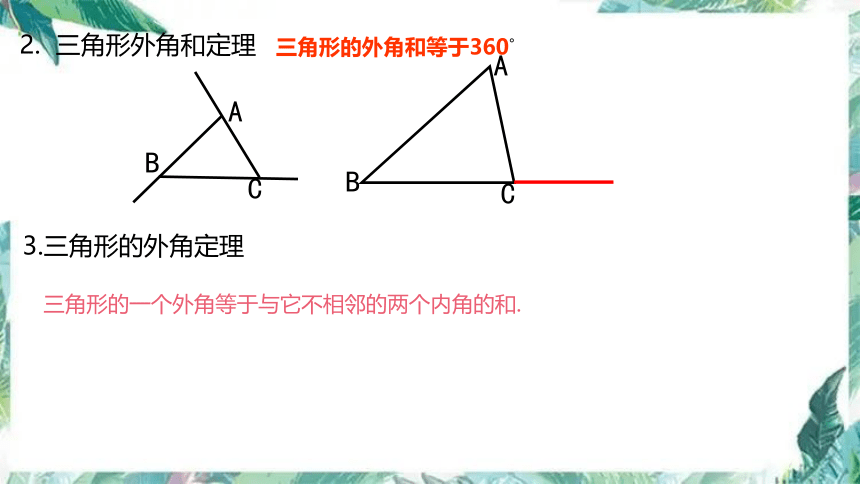
2. 三角形外角和定理
三角形的外角和等于360°
3.三角形的外角定理
三角形的一个外角等于与它不相邻的两个内角的和.
A
B
C
A
B
C
常见题型
2.一个三角形的三个外角之比为3:3:2,则这个三角形是( )A.等腰三角形 B. 等腰直角三角形 C.直角三角形 D.等边三角形
解法与上题同。解得,一份为22.50,三个内角分别为67.50,67.50,450.所以是等腰三角形,
1.如图,CD、BD分别平分∠ACE、∠ABC,∠A=80°,则∠BDC=( )
A.35° B.40° C.30° D.45°
B
3.如图,将三角板的直角顶点放在直角尺的一边上,∠1=30°,∠2=50°,则∠3的度数为( )
A.80° B. 50° C. 30 ° D. 20°
D
4.如图,在锐角△ABC中,CD、BE分别是AB、AC上的高,且CD、BE交于一点P,若∠A=500,则∠BPC的度数是( )A.150° B. 130° C. 120° D. 100°
解析:由CD、BE分别是AB上的高,∠A=50°,
可得∠ACD=40°
又BE分别是AC上的高,得∠PEC=90°。
由 ∠BPC=∠ACD+∠PEC
=40°+90°
=130°
B
5.填空:(1)△ABC中,若∠A+∠C=2∠B,则∠B=____; (2)△ABC中,若∠A:∠B:∠C=2:3:5,则∠A=___,∠B=____,∠C=____.(3)如图,直线a∥b,则∠A=____度。
600
360
540
900
390
6.已知:如图,在△ABC中,AD、AE分别是△ABC的高和角平分线。
(1)若∠B=30°,∠C=50°,求∠DAE的度数。(2)试问∠DAE与∠C-∠B有怎样的数量的关系?说明 理由
解析:(1)由∠B=300,∠C=500,∠B+∠C+∠BAC=1800,得∠BAC=1000.又知AE是△ABC的角平分线,
所以∠EAC= ∠BAC=500.
因为AD是△ABC的高线,所以∠ADC=900,根据直角三角形两锐角互余,可得∠CAD=400.所以∠EAD=∠EAC-∠DAC=100.
(2)说明方法同(1)∠DAE= (∠C-∠B)
7. 已知如图,O是△ABC内一点,且OB、OC分别平分∠ABC、∠ACB.(1)若∠A=46°,求∠BOC; (2)若∠A=n°,求∠BOC;(3)若∠BOC=148°,利用第(2)题的结论求∠A
解析:(1)由∠A+∠ABC+∠ACB=1800,∠A=460,得∠ABC+∠ACB=1340又因为OB、OC分别平分∠ABC、∠ACB.得:∠2= ∠ABC,∠4= ∠ACB,所以∠2+∠4= (∠ABC+∠ACB)=670.因为∠BOC+∠2+∠4=1800,所以∠BOC=1130
(2)将(1)中的460换成n0,进行推理计算可得∠BOC=900+ n0 (3)将∠BOC=1480代入(2)中的结论∠BOC=900+ ∠A得:∠A=1160
n边形内角和等于(n-2)×180 °(n ≥3的整数).
n边形的外角和等于360°.
正多边形的每个内角的度数是
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
正多边形的各个角都相等,各条边都相等的多边形.
n边形一个顶点引(n-3)条对角线,
考点3.多边形及其内角和
1.一个多边形的每个内角都等于144°,则这个多边形的边数是( )A. 8 B. 9 C. 10 D. 11
常见题型
解析:
法(1)设边数为n, 则有(n-2)·1800=n·144° 解得: n=10法(2)设边数为n,由每个内角为1440,可得每个外角为360,所以n·360=3600,
解得,n=10
2.若一个n边形的每一个外角都是36°,则这个n边形对角线的条数是( )A.30 B. 32 C. 35 D. 38
解析:由题意得n=10,共有对角线: 。
C
C
3.如图,AB∥CD,DE⊥BE,BF、DF分别为∠ABE、∠CDE的角平分线,则∠BFD=( )A.110° B. 120° C. 125° D. 135°
解析:由AB∥CD,得∠ABE+∠E+∠CDE=3600.又DE⊥BE,所以∠BED=900.所以∠ABE+∠CDE=2700,又因为BF、DF分别为∠ABE、∠CDE的角平分线,所以∠FBE= ∠ABE, ∠FDE= ∠CDE所以∠FBE+∠FDE= (∠ABE+∠CDE)=1350.
由∠ABE+∠CDE+∠BFD+∠E=3600.所以∠BFD=1350
4.如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
A.90° B. 135° C. 270° D. 315°
解析:由外角等于不相邻两个内角各,可得∠1+∠2=1800+900=2700.
D
C
5.如图,将边长相等的正方形、正五边形正六边形摆放在平面上,则∠1为( )A.32° B. 36° C. 40° D. 42°
解析:由多边形内角和定理,易求得正方形每个内角为900 ,正五边形每个内角为1080,正六边形每个内角为1200,又知道900+1200+1080+∠1=3600 所以∠1=420
6. 如果边长相等的正五边形和正方形的一边重合,那么∠1的度数是( )
A.30° B. 15° C. 18° D . 20°
解析:正方形每个内角为900,正五边形每个内角1080,所以∠1=1080-900=180
D
C
7.如图,小亮从点O出发,前进5m后向右转30°,再前进5m后又向右转30°,这样走n次后恰好回到点O处,小亮走出的这个n边形每个内角是___ 度,周长是__ 米
解析:小亮从点O出发,前进5m后向右转300,再前进5m后又向右转300,这样走n次后恰好回到点O处,经过的路径是正多边形。因为每个外角都是300,每个内角为1500.所以n=360÷30=12因为每次5m,知各边相等,周长 =12×5=70(m)
1500
70
综合提升
1.(1)如图①,△ABC中,点D、E在边BC上,AD平分∠BAC,AE⊥BC,∠B=35°,∠C=65°,求∠DAE的度数;(2)如图②,若把(1)中的条件“AE⊥BC”变成“F为DA延长线上一点,FE⊥BC”,其它条件不变,求∠DFE的度数;(3)若把(1)中的条件“AE⊥BC”变成“F为AD延长线上一点,FE⊥BC”,其它条件不变,请画出相应的图形,并求出∠DFE的度数;(4)结合上述三个问题的解决过程,你能得到什么结论?
解:(1)∠BAC=180°﹣∠B﹣∠C=180°﹣35°﹣65°=80°,∵AD平分∠BAC
∴∠BAD= ∠BAC=40°,
∵AE⊥BC,∴∠AEB=90°,∴∠BAE=90°﹣∠B=55°,∴∠DAE=∠BAE﹣∠BAD=55°﹣40°=15°;
(2)作AH⊥BC于H,如图②,由(1)得∠DAH=15°,∵FE⊥BC,∴AH∥EF,∴∠DFE=∠DAH=15°;(3)作AH⊥BC于H,如图③,由(1)得∠DAH=15°,∵FE⊥BC,∴AH∥EF,∴∠DFE=∠DAH=15°;
(4)结合上述三个问题的解决过程,得到∠BAC的角平分线与角平分线上的点作BC的垂线的夹角为15°.
2.如图,在△ABC中,点E在AC上,∠AEB=∠ABC.(1)图1中,作∠BAC的角平分线AD,分别交CB、BE于D、F两点,求证:∠EFD=∠ADC;(2)图2中,作△ABC的外角∠BAG的角平分线AD,分别交CB、BE的延长线于D、F两点,试探究(1)中结论是否仍成立?为什么?
解:(1)∵AD平分∠BAC,∴∠BAD=∠DAC,∵∠EFD=∠DAC+∠AEB,∠ADC=∠ABC+∠BAD,又∵∠AEB=∠ABC,∴∠EFD=∠ADC; (2)探究(1)中结论仍成立;理由:∵AD平分∠BAG,∴∠BAD=∠GAD,∵∠FAE=∠GAD,∴∠FAE=∠BAD,∵∠EFD=∠AEB﹣∠FAE,∠ADC=∠ABC﹣∠BAD,又∵∠AEB=∠ABC,∴∠EFD=∠ADC.
第十一章 三角形 (复习课)
三角形
三角形有
关的线段
三角形内角和
三角形外角和
三角形知识结构图
三角形的边
高线
中线
角平分线
三角形
有关的角
内角与外角关系
三角形的分类
多边形与镶嵌
1. 三角形的三边关系:
(1) 三角形两边的和大于第三边
2. 判断三条已知线段a、b、c能否组成三角形.
较短两边之和大于第三边
3. 确定三角形第三边的取值范围:
两边之差<第三边<两边之和.
(2) 三角形两边的差小于第三边
考点1.与三角形有关的线段
连结三角形一个顶点与它对边中点 的线段叫做三角形的中线。
三角形一个角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线。
从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高线.
4. 三角形的主要线段
5. 三角形具有稳定性,而四边形没有稳定性。
常见考点
1.在下列长度的三条线段中,不能组成三角形的是( )A. 2cm ,3cm ,4 cm B. 3cm ,6cm,7cm
C. 2cm,2cm,6cm D. 5cm,6cm,7cm.
2. 已知三角形两边长分别为1,5,第三边长为整数,则第三边的长为_________。
C
5
3.下列说法中,正确的是( )A. 三角形的角平线是射线
B. 三角形的高总在三角形的内部
C.三角形的高、中线、角平分线一定是三条不同的线段
D.三角形的中线在三角形的内部
D
4.下图中AE是△ABC的高线,作图正确的是( )
C
5.如图,在△ABC中,D、E分别为BC,AD的中点,且S△ABC=4,则S阴影 =___.
1
解析:由D、E分别为BC,AD的中点,根据等底同高的两个三角形面积相等,可得:
S△ADC= S△ABC, S△AEC= S△ADC
所以,S△AEC= S△ABC=1。
6. 已知等腰三角形的一边等于8cm,一边等于6cm,则三角形的周长为______________
解析:此题分为两种情况(1)以8cm为腰,6cm为底,则三角形的周长=2×8+6=22(cm)(2)以6cm为腰,8cm为底,则三角形的周长=2×6+8=20(cm)故三角形的周长为22cm或20cm
7.木工师傅在做完门框后,为防止变形,常常像如图所示那样钉上两条斜拉的木板条(即图中的AB、CD两根木条),这样做的数学道理是_____________。
22cm或20cm
三角形的稳定性
1. 三角形内角和定理
三角形的内角和等于1800
直角三角形的两个锐角互余。
A
B
C
考点2.与三角形有关的角
2. 三角形外角和定理
三角形的外角和等于360°
3.三角形的外角定理
三角形的一个外角等于与它不相邻的两个内角的和.
A
B
C
A
B
C
常见题型
2.一个三角形的三个外角之比为3:3:2,则这个三角形是( )A.等腰三角形 B. 等腰直角三角形 C.直角三角形 D.等边三角形
解法与上题同。解得,一份为22.50,三个内角分别为67.50,67.50,450.所以是等腰三角形,
1.如图,CD、BD分别平分∠ACE、∠ABC,∠A=80°,则∠BDC=( )
A.35° B.40° C.30° D.45°
B
3.如图,将三角板的直角顶点放在直角尺的一边上,∠1=30°,∠2=50°,则∠3的度数为( )
A.80° B. 50° C. 30 ° D. 20°
D
4.如图,在锐角△ABC中,CD、BE分别是AB、AC上的高,且CD、BE交于一点P,若∠A=500,则∠BPC的度数是( )A.150° B. 130° C. 120° D. 100°
解析:由CD、BE分别是AB上的高,∠A=50°,
可得∠ACD=40°
又BE分别是AC上的高,得∠PEC=90°。
由 ∠BPC=∠ACD+∠PEC
=40°+90°
=130°
B
5.填空:(1)△ABC中,若∠A+∠C=2∠B,则∠B=____; (2)△ABC中,若∠A:∠B:∠C=2:3:5,则∠A=___,∠B=____,∠C=____.(3)如图,直线a∥b,则∠A=____度。
600
360
540
900
390
6.已知:如图,在△ABC中,AD、AE分别是△ABC的高和角平分线。
(1)若∠B=30°,∠C=50°,求∠DAE的度数。(2)试问∠DAE与∠C-∠B有怎样的数量的关系?说明 理由
解析:(1)由∠B=300,∠C=500,∠B+∠C+∠BAC=1800,得∠BAC=1000.又知AE是△ABC的角平分线,
所以∠EAC= ∠BAC=500.
因为AD是△ABC的高线,所以∠ADC=900,根据直角三角形两锐角互余,可得∠CAD=400.所以∠EAD=∠EAC-∠DAC=100.
(2)说明方法同(1)∠DAE= (∠C-∠B)
7. 已知如图,O是△ABC内一点,且OB、OC分别平分∠ABC、∠ACB.(1)若∠A=46°,求∠BOC; (2)若∠A=n°,求∠BOC;(3)若∠BOC=148°,利用第(2)题的结论求∠A
解析:(1)由∠A+∠ABC+∠ACB=1800,∠A=460,得∠ABC+∠ACB=1340又因为OB、OC分别平分∠ABC、∠ACB.得:∠2= ∠ABC,∠4= ∠ACB,所以∠2+∠4= (∠ABC+∠ACB)=670.因为∠BOC+∠2+∠4=1800,所以∠BOC=1130
(2)将(1)中的460换成n0,进行推理计算可得∠BOC=900+ n0 (3)将∠BOC=1480代入(2)中的结论∠BOC=900+ ∠A得:∠A=1160
n边形内角和等于(n-2)×180 °(n ≥3的整数).
n边形的外角和等于360°.
正多边形的每个内角的度数是
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
正多边形的各个角都相等,各条边都相等的多边形.
n边形一个顶点引(n-3)条对角线,
考点3.多边形及其内角和
1.一个多边形的每个内角都等于144°,则这个多边形的边数是( )A. 8 B. 9 C. 10 D. 11
常见题型
解析:
法(1)设边数为n, 则有(n-2)·1800=n·144° 解得: n=10法(2)设边数为n,由每个内角为1440,可得每个外角为360,所以n·360=3600,
解得,n=10
2.若一个n边形的每一个外角都是36°,则这个n边形对角线的条数是( )A.30 B. 32 C. 35 D. 38
解析:由题意得n=10,共有对角线: 。
C
C
3.如图,AB∥CD,DE⊥BE,BF、DF分别为∠ABE、∠CDE的角平分线,则∠BFD=( )A.110° B. 120° C. 125° D. 135°
解析:由AB∥CD,得∠ABE+∠E+∠CDE=3600.又DE⊥BE,所以∠BED=900.所以∠ABE+∠CDE=2700,又因为BF、DF分别为∠ABE、∠CDE的角平分线,所以∠FBE= ∠ABE, ∠FDE= ∠CDE所以∠FBE+∠FDE= (∠ABE+∠CDE)=1350.
由∠ABE+∠CDE+∠BFD+∠E=3600.所以∠BFD=1350
4.如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
A.90° B. 135° C. 270° D. 315°
解析:由外角等于不相邻两个内角各,可得∠1+∠2=1800+900=2700.
D
C
5.如图,将边长相等的正方形、正五边形正六边形摆放在平面上,则∠1为( )A.32° B. 36° C. 40° D. 42°
解析:由多边形内角和定理,易求得正方形每个内角为900 ,正五边形每个内角为1080,正六边形每个内角为1200,又知道900+1200+1080+∠1=3600 所以∠1=420
6. 如果边长相等的正五边形和正方形的一边重合,那么∠1的度数是( )
A.30° B. 15° C. 18° D . 20°
解析:正方形每个内角为900,正五边形每个内角1080,所以∠1=1080-900=180
D
C
7.如图,小亮从点O出发,前进5m后向右转30°,再前进5m后又向右转30°,这样走n次后恰好回到点O处,小亮走出的这个n边形每个内角是___ 度,周长是__ 米
解析:小亮从点O出发,前进5m后向右转300,再前进5m后又向右转300,这样走n次后恰好回到点O处,经过的路径是正多边形。因为每个外角都是300,每个内角为1500.所以n=360÷30=12因为每次5m,知各边相等,周长 =12×5=70(m)
1500
70
综合提升
1.(1)如图①,△ABC中,点D、E在边BC上,AD平分∠BAC,AE⊥BC,∠B=35°,∠C=65°,求∠DAE的度数;(2)如图②,若把(1)中的条件“AE⊥BC”变成“F为DA延长线上一点,FE⊥BC”,其它条件不变,求∠DFE的度数;(3)若把(1)中的条件“AE⊥BC”变成“F为AD延长线上一点,FE⊥BC”,其它条件不变,请画出相应的图形,并求出∠DFE的度数;(4)结合上述三个问题的解决过程,你能得到什么结论?
解:(1)∠BAC=180°﹣∠B﹣∠C=180°﹣35°﹣65°=80°,∵AD平分∠BAC
∴∠BAD= ∠BAC=40°,
∵AE⊥BC,∴∠AEB=90°,∴∠BAE=90°﹣∠B=55°,∴∠DAE=∠BAE﹣∠BAD=55°﹣40°=15°;
(2)作AH⊥BC于H,如图②,由(1)得∠DAH=15°,∵FE⊥BC,∴AH∥EF,∴∠DFE=∠DAH=15°;(3)作AH⊥BC于H,如图③,由(1)得∠DAH=15°,∵FE⊥BC,∴AH∥EF,∴∠DFE=∠DAH=15°;
(4)结合上述三个问题的解决过程,得到∠BAC的角平分线与角平分线上的点作BC的垂线的夹角为15°.
2.如图,在△ABC中,点E在AC上,∠AEB=∠ABC.(1)图1中,作∠BAC的角平分线AD,分别交CB、BE于D、F两点,求证:∠EFD=∠ADC;(2)图2中,作△ABC的外角∠BAG的角平分线AD,分别交CB、BE的延长线于D、F两点,试探究(1)中结论是否仍成立?为什么?
解:(1)∵AD平分∠BAC,∴∠BAD=∠DAC,∵∠EFD=∠DAC+∠AEB,∠ADC=∠ABC+∠BAD,又∵∠AEB=∠ABC,∴∠EFD=∠ADC; (2)探究(1)中结论仍成立;理由:∵AD平分∠BAG,∴∠BAD=∠GAD,∵∠FAE=∠GAD,∴∠FAE=∠BAD,∵∠EFD=∠AEB﹣∠FAE,∠ADC=∠ABC﹣∠BAD,又∵∠AEB=∠ABC,∴∠EFD=∠ADC.
