沪科版八年级数学上册 13.1三角形中的边角关系 三角形的内角和 一课一练(含答案)
文档属性
| 名称 | 沪科版八年级数学上册 13.1三角形中的边角关系 三角形的内角和 一课一练(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 86.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-14 00:00:00 | ||
图片预览



文档简介
13.1三角形中的边角关系--三角形的内角和
一、选择题
1.已知△ABC中,∠A=70°,∠B=60°,则∠C=( )
A.50° B.60° C.70° D.80°
2.若三角形三个内角度数比为2:3:4,则这个三角形一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
3.如图,将△ABC纸片沿DE折叠,点A的对应点为A′,若∠B=60°,∠C=80°,则∠1+∠2等于( )
A.40° B.60° C.80° D.140°
4.如图,AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=76°,∠C=64°,则∠DAE的度数是( )
A.10° B.12° C.15° D.18°
5.在下列条件中,能确定△ABC是直角三角形的条件有( )
①∠A+∠B=∠C,
②∠A:∠B:∠C=1:2:3,
③∠A=90°﹣∠B,
④∠A=∠B=∠C,
A.1个 B.2个 C.3个 D.4个
6.如图,三角形ABC,∠BAC=90°,AD是三角形ABC的高,图中相等的是( )
A.∠B=∠C B.∠BAD=∠B C.∠C=∠BAD D.∠DAC=∠C
7.具备下列条件的△ABC,不是直角三角形的是( )
A.∠A+∠B=∠C B.∠A∠B∠C
C.∠A=2∠B=3∠C D.∠A:∠B:∠C=1:3:4
8.如图,在△ABC中,∠A=50°,∠1=30°,∠2=40°,∠D的度数是( )
A.110° B.120° C.130° D.140°
9.如图,将△ABC沿着DE翻折,使B点与B′点重合,若∠1+∠2=80°,则∠B的度数为( )
A.20° B.30° C.40° D.50°
10.如图,BF是∠ABD的平分线,CE是∠ACD的平分线,BF与CE交于G,若∠BDC=130°,∠BGC=100°,则∠A的度数为( )
A.60° B.70° C.80° D.90°
二、填空题
11.如图,∠1=20°,∠2=24°,∠A=36°,∠BDC= 度.
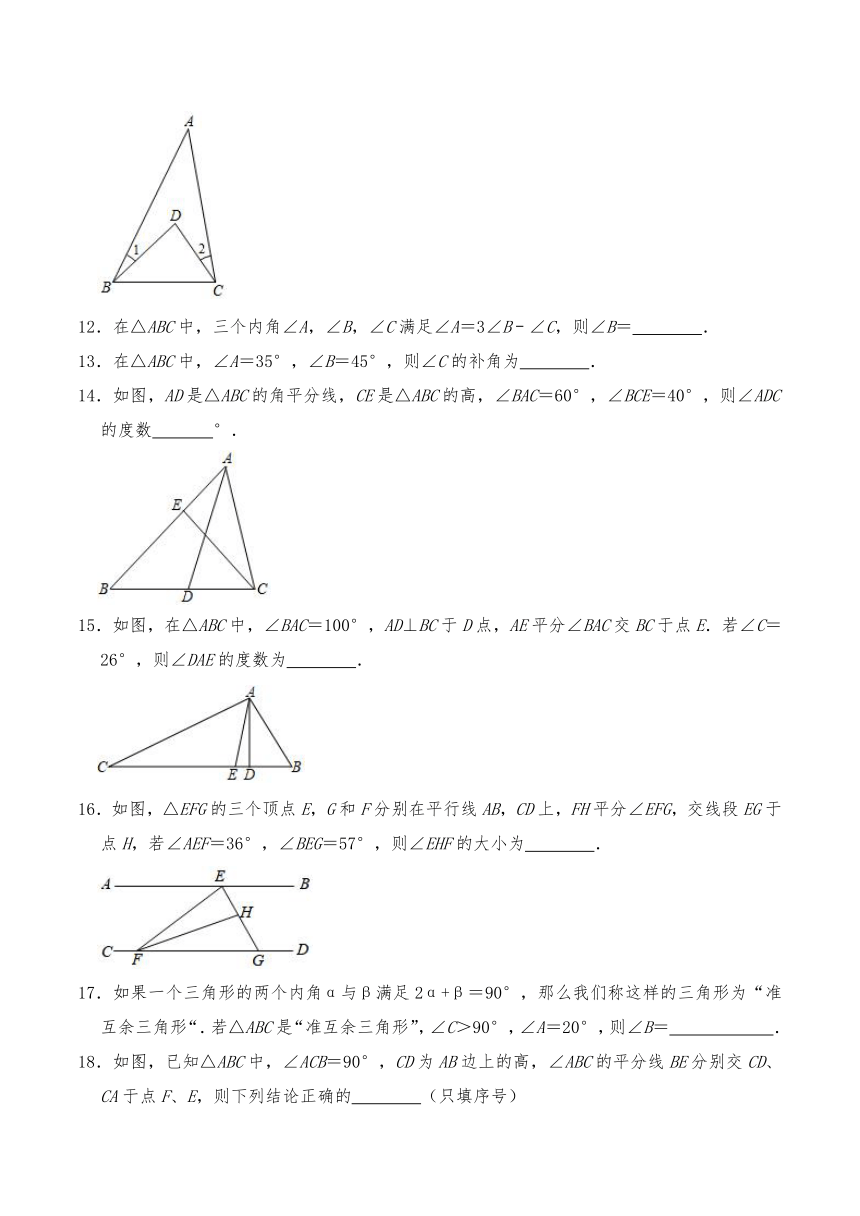
12.在△ABC中,三个内角∠A,∠B,∠C满足∠A=3∠B﹣∠C,则∠B= .
13.在△ABC中,∠A=35°,∠B=45°,则∠C的补角为 .
14.如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,则∠ADC的度数 °.
15.如图,在△ABC中,∠BAC=100°,AD⊥BC于D点,AE平分∠BAC交BC于点E.若∠C=26°,则∠DAE的度数为 .
16.如图,△EFG的三个顶点E,G和F分别在平行线AB,CD上,FH平分∠EFG,交线段EG于点H,若∠AEF=36°,∠BEG=57°,则∠EHF的大小为 .
17.如果一个三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形“.若△ABC是“准互余三角形”,∠C>90°,∠A=20°,则∠B= .
18.如图,已知△ABC中,∠ACB=90°,CD为AB边上的高,∠ABC的平分线BE分别交CD、CA于点F、E,则下列结论正确的 (只填序号)
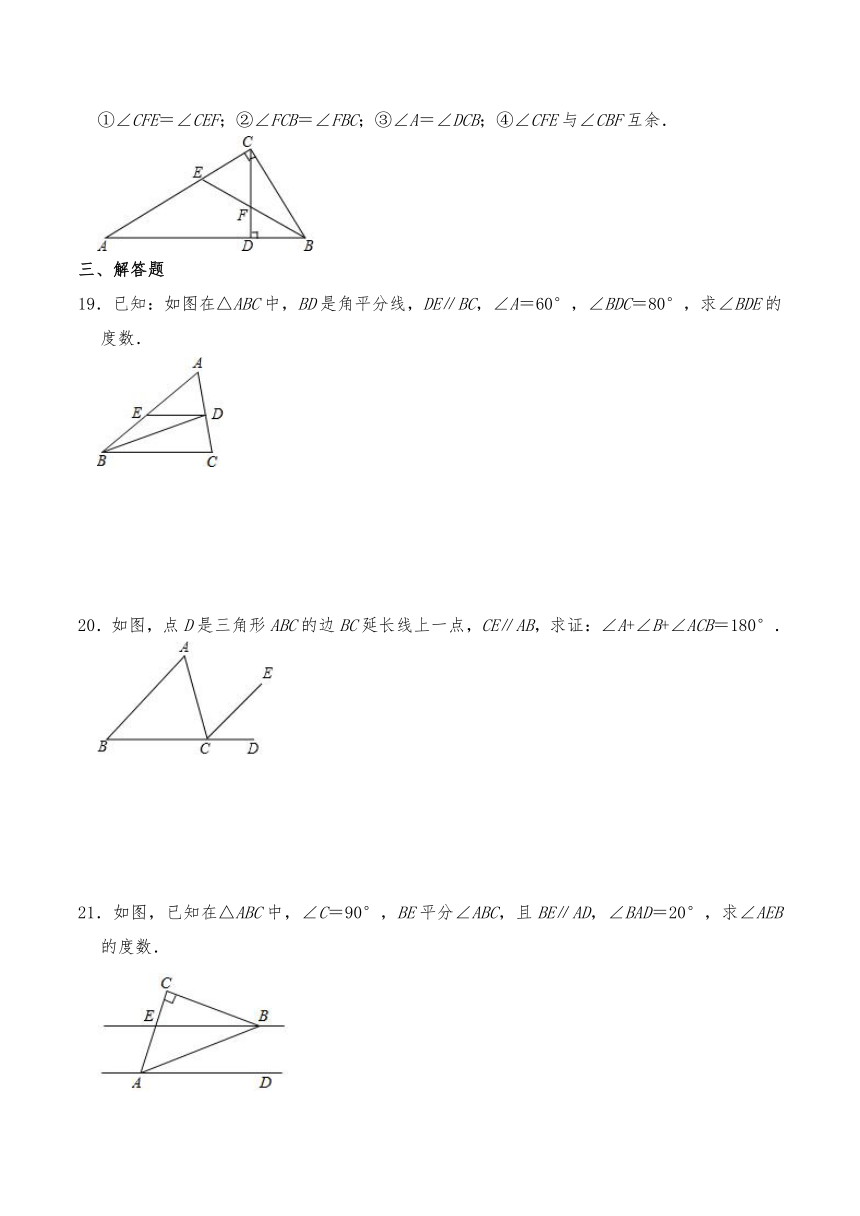
①∠CFE=∠CEF;②∠FCB=∠FBC;③∠A=∠DCB;④∠CFE与∠CBF互余.
三、解答题
19.已知:如图在△ABC中,BD是角平分线,DE∥BC,∠A=60°,∠BDC=80°,求∠BDE的度数.
20.如图,点D是三角形ABC的边BC延长线上一点,CE∥AB,求证:∠A+∠B+∠ACB=180°.
21.如图,已知在△ABC中,∠C=90°,BE平分∠ABC,且BE∥AD,∠BAD=20°,求∠AEB的度数.
22.如图,△ABC中,高BD、CE相交于点H,若∠A:∠ABC:∠ACB=3:2:4,则∠BHC为多少度?
23.如图,BE是∠ABC的平分线,AE⊥AD,点C和点D在直线AB的同侧,设∠ABE=α,∠BAE=β.
(1)若AD∥BC,探索α,β满足的数量关系,并说明理由.
(2)若BE⊥AE,且β=2α,求∠ABC的度数.
(3)设γ=∠DAB+∠ABC﹣180°,若γ=17°,且α+3β=125°,求3α+4β的度数.
24.已知:△ABC中,AE是△ABC的角平分线,AD是△ABC的BC边上的高,过点B做BF∥AE,交直线AD于点F.
(1)如图1,若∠ABC=70°,∠C=30°,则∠AFB= ;
(2)若(1)中的∠ABC=α,∠ACB=β,则∠AFB= ;(用α,β表示)
(3)如图2,(2)中的结论还成立吗?若成立,说明理由;若不成立,请求出∠AFB.(用α,β表示)
答案
一、选择题
A.A.C.B.C.C.C.B.C.B.
二、填空题
11.80.
12.45°.
13.80°.
14.80.
15.14°.
16.75°.
17.35°或50°.
18.①③④.
三、解答题
19.∵∠A=60°,∠BDC=80°,∠BDC=∠A+∠ABD,
∴∠ABD=20°,
∵BD是角平分线,
∴∠ABD=∠DBC=20°,
∵DE∥BC,
∴∠EDB=∠DBC=20°,
即∠BDE的度数是20°.
20.证明:∵CE∥AB,
∴∠A=∠ACE∠B=∠DCE,
∵∠ACE+∠DCE+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
21.∵BE∥AD,
∴∠ABE=∠BAD=20°,
∵BE平分∠ABC,
∴∠EBC=∠ABE=20°,
∵∠C=90°,
∴∠AEB=∠C+∠CBE=90°+20°=110°.
22.∵在△ABC中,∠A:∠ABC:∠ACB=3:2:4,
故设∠A=3x,∠ABC=2x,∠ACB=4x.
∵在△ABC中,∠A+∠ABC+∠ACB=180°,
∴3x+2x+4x=180°,
解得x=20°,
∴∠A=3x=60°.
∵BD,CE分别是边AC,AB上的高,
∴∠ADB=90°,∠BEC=90°,
∴在△ABD中,∠ABD=180°﹣∠ADB﹣∠A=180°﹣90°﹣60°=30°,
∴∠BHC=∠ABD+∠BEC=30°+90°=120°.
23.(1)如图1中,延长AE交BC于F.
∵AD∥BC,AE⊥AD,
∴AF⊥BC,
∴∠AFB=90°,
∵BE平分∠ABC,
∴∠ABF=2α,
∴∠ABF+∠BAF=90°,
∴2α+β=90°.
(2)如图2中,
∵AE⊥BE,
∴∠E=90°,
∴α+β=90°,
∵β=2α,
∴α=30°,
∴∠ABC=2α=60°.
(3)由题意:90°+β+2α=180°+17° ①
α+3β=125° ②,
①+②可得3α+4β=232°.
24.(1)∵∠ABC=70°,∠C=30°,∠ABC+∠C+∠BAC=180°,
∴∠BAC=180°﹣70°﹣30°=80°,
∵AE是△ABC的角平分线,
∴∠BAE∠BAC=40°,
∵AD是△ABC的BC边上的高,
∴∠ADB=90°,
∴∠BAD=90°﹣∠ABC=90°﹣70°=20°,
∴∠EAD=∠BAE﹣∠BAD=40°﹣20°=20°,
∵BF∥AE,
∴∠AFB=∠EAD=20°,
故答案为20°;
(2)∵∠ABC=α,∠C=β,∠ABC+∠C+∠BAC=180°,
∴∠BAC=180°﹣α﹣β,
∵AE是△ABC的角平分线,
∴∠BAE∠BAC,
∵AD是△ABC的BC边上的高,
∴∠ADB=90°,
∴∠BAD=90°﹣∠ABC=90°﹣α,
∴∠EAD=∠BAE﹣∠BAD(90°﹣α),
∵BF∥AE,
∴∠AFB=∠EAD,
故答案为;
(3)不成立,
∵∠ABC=α,∠C=β,∠ABC+∠C+∠BAC=180°,
∴∠BAC=180°﹣α﹣β,∠ABD=180°﹣α,
∵AE是△ABC的角平分线,
∴∠BAE∠BAC,
∵AD是△ABC的BC边上的高,
∴∠ADB=90°,
∴∠BAD=90°﹣∠ABD=90°﹣(180°﹣α)=α﹣90°,
∴EAD=∠BAE+∠BAD(α﹣90°),
∵BF∥AE,
∴∠AFB+∠EAD=180°,
∴∠AFB=180°.
一、选择题
1.已知△ABC中,∠A=70°,∠B=60°,则∠C=( )
A.50° B.60° C.70° D.80°
2.若三角形三个内角度数比为2:3:4,则这个三角形一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
3.如图,将△ABC纸片沿DE折叠,点A的对应点为A′,若∠B=60°,∠C=80°,则∠1+∠2等于( )
A.40° B.60° C.80° D.140°
4.如图,AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=76°,∠C=64°,则∠DAE的度数是( )
A.10° B.12° C.15° D.18°
5.在下列条件中,能确定△ABC是直角三角形的条件有( )
①∠A+∠B=∠C,
②∠A:∠B:∠C=1:2:3,
③∠A=90°﹣∠B,
④∠A=∠B=∠C,
A.1个 B.2个 C.3个 D.4个
6.如图,三角形ABC,∠BAC=90°,AD是三角形ABC的高,图中相等的是( )
A.∠B=∠C B.∠BAD=∠B C.∠C=∠BAD D.∠DAC=∠C
7.具备下列条件的△ABC,不是直角三角形的是( )
A.∠A+∠B=∠C B.∠A∠B∠C
C.∠A=2∠B=3∠C D.∠A:∠B:∠C=1:3:4
8.如图,在△ABC中,∠A=50°,∠1=30°,∠2=40°,∠D的度数是( )
A.110° B.120° C.130° D.140°
9.如图,将△ABC沿着DE翻折,使B点与B′点重合,若∠1+∠2=80°,则∠B的度数为( )
A.20° B.30° C.40° D.50°
10.如图,BF是∠ABD的平分线,CE是∠ACD的平分线,BF与CE交于G,若∠BDC=130°,∠BGC=100°,则∠A的度数为( )
A.60° B.70° C.80° D.90°
二、填空题
11.如图,∠1=20°,∠2=24°,∠A=36°,∠BDC= 度.
12.在△ABC中,三个内角∠A,∠B,∠C满足∠A=3∠B﹣∠C,则∠B= .
13.在△ABC中,∠A=35°,∠B=45°,则∠C的补角为 .
14.如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,则∠ADC的度数 °.
15.如图,在△ABC中,∠BAC=100°,AD⊥BC于D点,AE平分∠BAC交BC于点E.若∠C=26°,则∠DAE的度数为 .
16.如图,△EFG的三个顶点E,G和F分别在平行线AB,CD上,FH平分∠EFG,交线段EG于点H,若∠AEF=36°,∠BEG=57°,则∠EHF的大小为 .
17.如果一个三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形“.若△ABC是“准互余三角形”,∠C>90°,∠A=20°,则∠B= .
18.如图,已知△ABC中,∠ACB=90°,CD为AB边上的高,∠ABC的平分线BE分别交CD、CA于点F、E,则下列结论正确的 (只填序号)
①∠CFE=∠CEF;②∠FCB=∠FBC;③∠A=∠DCB;④∠CFE与∠CBF互余.
三、解答题
19.已知:如图在△ABC中,BD是角平分线,DE∥BC,∠A=60°,∠BDC=80°,求∠BDE的度数.
20.如图,点D是三角形ABC的边BC延长线上一点,CE∥AB,求证:∠A+∠B+∠ACB=180°.
21.如图,已知在△ABC中,∠C=90°,BE平分∠ABC,且BE∥AD,∠BAD=20°,求∠AEB的度数.
22.如图,△ABC中,高BD、CE相交于点H,若∠A:∠ABC:∠ACB=3:2:4,则∠BHC为多少度?
23.如图,BE是∠ABC的平分线,AE⊥AD,点C和点D在直线AB的同侧,设∠ABE=α,∠BAE=β.
(1)若AD∥BC,探索α,β满足的数量关系,并说明理由.
(2)若BE⊥AE,且β=2α,求∠ABC的度数.
(3)设γ=∠DAB+∠ABC﹣180°,若γ=17°,且α+3β=125°,求3α+4β的度数.
24.已知:△ABC中,AE是△ABC的角平分线,AD是△ABC的BC边上的高,过点B做BF∥AE,交直线AD于点F.
(1)如图1,若∠ABC=70°,∠C=30°,则∠AFB= ;
(2)若(1)中的∠ABC=α,∠ACB=β,则∠AFB= ;(用α,β表示)
(3)如图2,(2)中的结论还成立吗?若成立,说明理由;若不成立,请求出∠AFB.(用α,β表示)
答案
一、选择题
A.A.C.B.C.C.C.B.C.B.
二、填空题
11.80.
12.45°.
13.80°.
14.80.
15.14°.
16.75°.
17.35°或50°.
18.①③④.
三、解答题
19.∵∠A=60°,∠BDC=80°,∠BDC=∠A+∠ABD,
∴∠ABD=20°,
∵BD是角平分线,
∴∠ABD=∠DBC=20°,
∵DE∥BC,
∴∠EDB=∠DBC=20°,
即∠BDE的度数是20°.
20.证明:∵CE∥AB,
∴∠A=∠ACE∠B=∠DCE,
∵∠ACE+∠DCE+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
21.∵BE∥AD,
∴∠ABE=∠BAD=20°,
∵BE平分∠ABC,
∴∠EBC=∠ABE=20°,
∵∠C=90°,
∴∠AEB=∠C+∠CBE=90°+20°=110°.
22.∵在△ABC中,∠A:∠ABC:∠ACB=3:2:4,
故设∠A=3x,∠ABC=2x,∠ACB=4x.
∵在△ABC中,∠A+∠ABC+∠ACB=180°,
∴3x+2x+4x=180°,
解得x=20°,
∴∠A=3x=60°.
∵BD,CE分别是边AC,AB上的高,
∴∠ADB=90°,∠BEC=90°,
∴在△ABD中,∠ABD=180°﹣∠ADB﹣∠A=180°﹣90°﹣60°=30°,
∴∠BHC=∠ABD+∠BEC=30°+90°=120°.
23.(1)如图1中,延长AE交BC于F.
∵AD∥BC,AE⊥AD,
∴AF⊥BC,
∴∠AFB=90°,
∵BE平分∠ABC,
∴∠ABF=2α,
∴∠ABF+∠BAF=90°,
∴2α+β=90°.
(2)如图2中,
∵AE⊥BE,
∴∠E=90°,
∴α+β=90°,
∵β=2α,
∴α=30°,
∴∠ABC=2α=60°.
(3)由题意:90°+β+2α=180°+17° ①
α+3β=125° ②,
①+②可得3α+4β=232°.
24.(1)∵∠ABC=70°,∠C=30°,∠ABC+∠C+∠BAC=180°,
∴∠BAC=180°﹣70°﹣30°=80°,
∵AE是△ABC的角平分线,
∴∠BAE∠BAC=40°,
∵AD是△ABC的BC边上的高,
∴∠ADB=90°,
∴∠BAD=90°﹣∠ABC=90°﹣70°=20°,
∴∠EAD=∠BAE﹣∠BAD=40°﹣20°=20°,
∵BF∥AE,
∴∠AFB=∠EAD=20°,
故答案为20°;
(2)∵∠ABC=α,∠C=β,∠ABC+∠C+∠BAC=180°,
∴∠BAC=180°﹣α﹣β,
∵AE是△ABC的角平分线,
∴∠BAE∠BAC,
∵AD是△ABC的BC边上的高,
∴∠ADB=90°,
∴∠BAD=90°﹣∠ABC=90°﹣α,
∴∠EAD=∠BAE﹣∠BAD(90°﹣α),
∵BF∥AE,
∴∠AFB=∠EAD,
故答案为;
(3)不成立,
∵∠ABC=α,∠C=β,∠ABC+∠C+∠BAC=180°,
∴∠BAC=180°﹣α﹣β,∠ABD=180°﹣α,
∵AE是△ABC的角平分线,
∴∠BAE∠BAC,
∵AD是△ABC的BC边上的高,
∴∠ADB=90°,
∴∠BAD=90°﹣∠ABD=90°﹣(180°﹣α)=α﹣90°,
∴EAD=∠BAE+∠BAD(α﹣90°),
∵BF∥AE,
∴∠AFB+∠EAD=180°,
∴∠AFB=180°.
