2022-2023学年人教版九年级数学上册24.4 弧长和扇形面积 课时练习(含解析)
文档属性
| 名称 | 2022-2023学年人教版九年级数学上册24.4 弧长和扇形面积 课时练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-14 13:14:05 | ||
图片预览

文档简介
24.4 弧长和扇形面积(附解析)
一、单选题(共10个小题)
1.一个圆锥侧面展开图的扇形的弧长为,则这个圆锥底面圆的半径为( )
A.6 B.12 C.24 D.2
2.如图,AB切⊙O于点B,连接OA交⊙O于点C,连接OB.若,OA=4,则劣弧的长是( )
A.π B.π C.π D.π
3.75°的圆心角所对的弧长是2.5πcm,则此弧所在圆的半径是( )
A.6cm B.7cm C.8cm D.9cm
4.一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如图),那么B点从开始至结束所走过的路径长度为( )
A. B. C.4 D.
5.如图,在半径为,圆心角等于45°的扇形AOB内部作一个正方形CDEF,使点C在OA上,点D、E在OB上,点F在上,则阴影部分的面积为(结果保留π)( )
A. B. C. D.
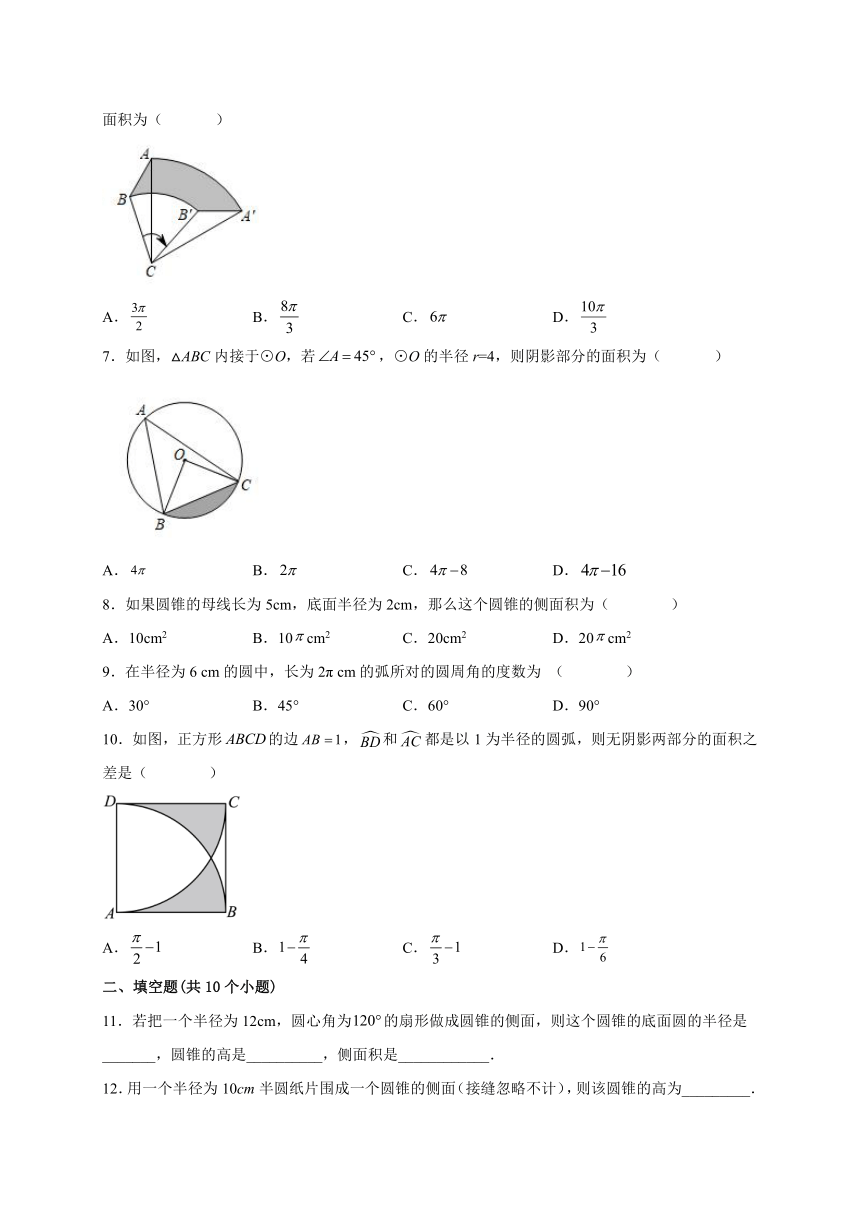
6.如图,将绕点旋转得到,已知,,则线段扫过的图形面积为( )
A. B. C. D.
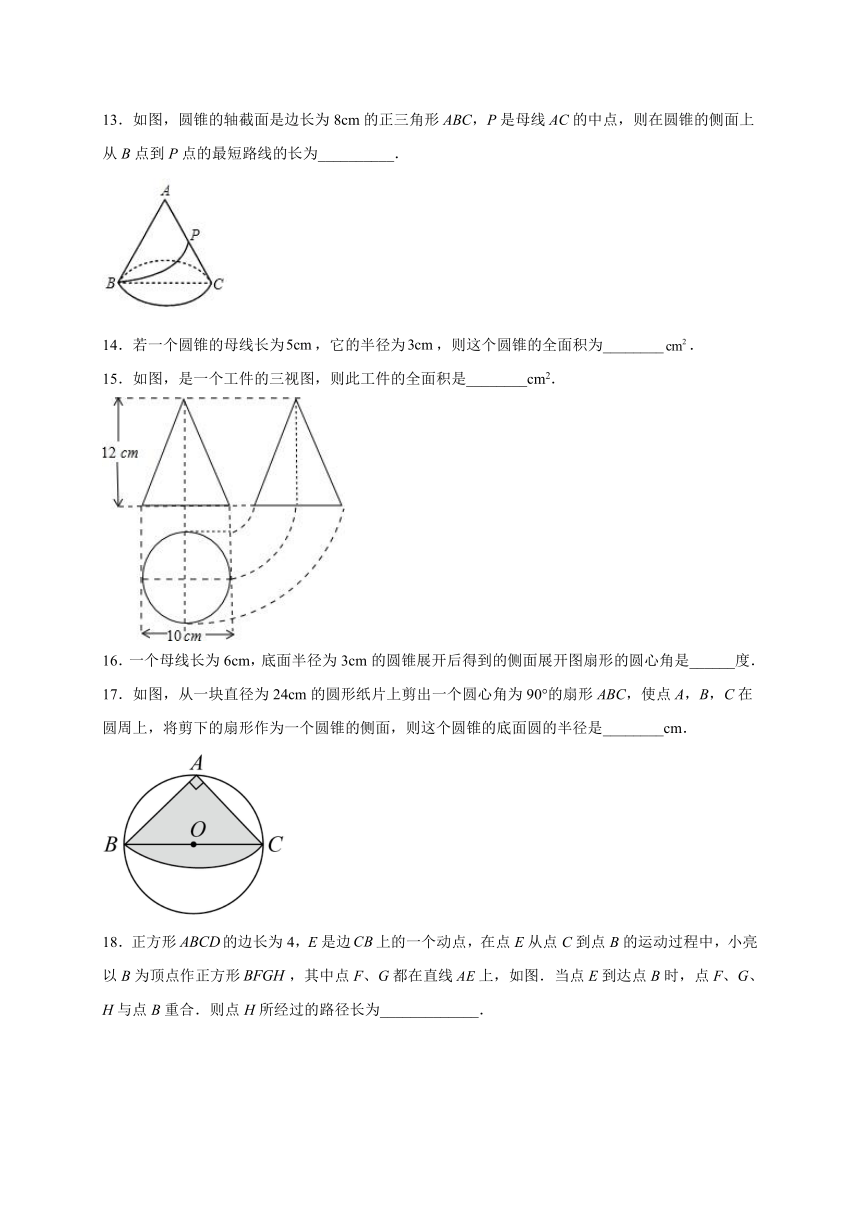
7.如图,△ABC内接于⊙O,若,⊙O的半径r=4,则阴影部分的面积为( )
A. B. C. D.
8.如果圆锥的母线长为5cm,底面半径为2cm,那么这个圆锥的侧面积为( )
A.10cm2 B.10cm2 C.20cm2 D.20cm2
9.在半径为6 cm的圆中,长为2π cm的弧所对的圆周角的度数为 ( )
A.30° B.45° C.60° D.90°
10.如图,正方形的边,和都是以1为半径的圆弧,则无阴影两部分的面积之差是( )
A. B. C. D.
二、填空题(共10个小题)
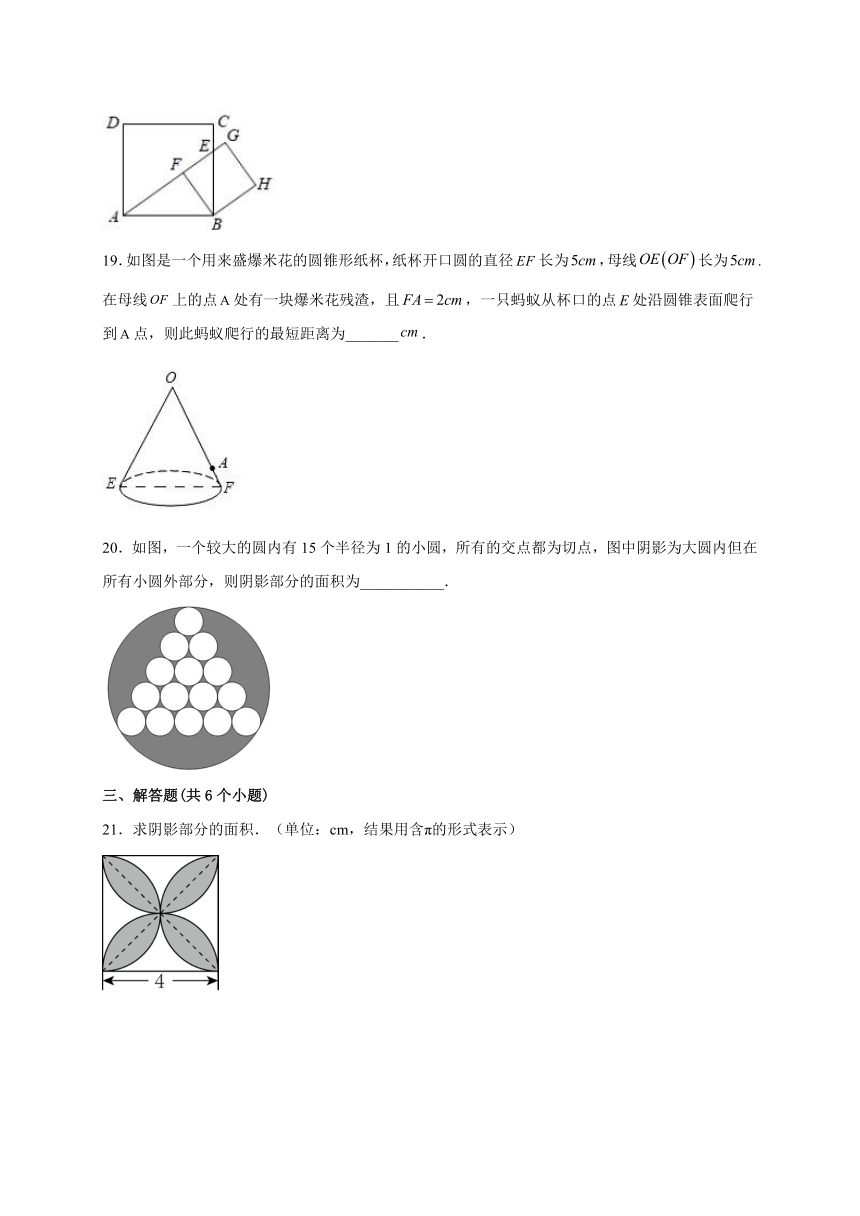
11.若把一个半径为12cm,圆心角为的扇形做成圆锥的侧面,则这个圆锥的底面圆的半径是_______,圆锥的高是__________,侧面积是____________.
12.用一个半径为10cm半圆纸片围成一个圆锥的侧面(接缝忽略不计),则该圆锥的高为_________.
13.如图,圆锥的轴截面是边长为8cm的正三角形ABC,P是母线AC的中点,则在圆锥的侧面上从B点到P点的最短路线的长为__________.
14.若一个圆锥的母线长为,它的半径为,则这个圆锥的全面积为________.
15.如图,是一个工件的三视图,则此工件的全面积是________cm2.
16.一个母线长为6cm,底面半径为3cm的圆锥展开后得到的侧面展开图扇形的圆心角是______度.
17.如图,从一块直径为24cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是________cm.
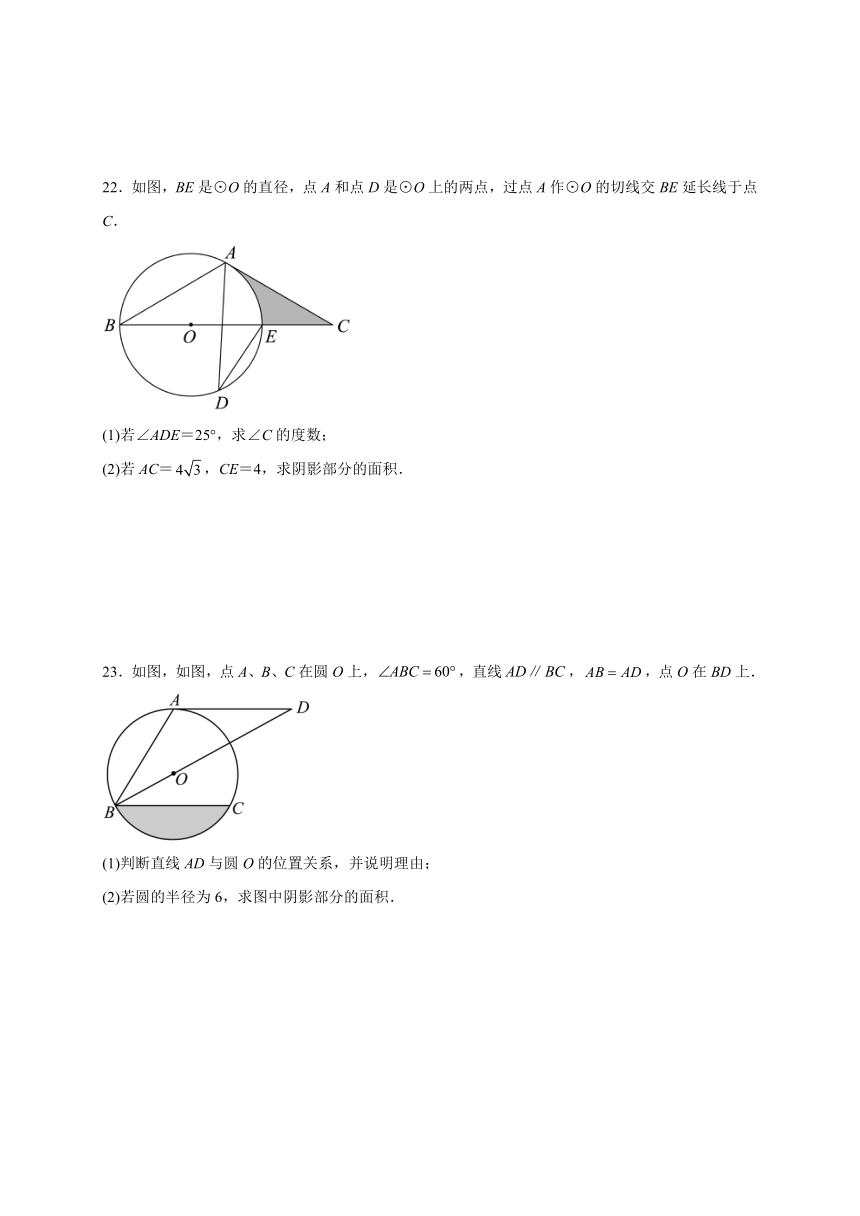
18.正方形的边长为4,E是边上的一个动点,在点E从点C到点B的运动过程中,小亮以B为顶点作正方形,其中点F、G都在直线上,如图.当点E到达点B时,点F、G、H与点B重合.则点H所经过的路径长为_____________.
19.如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径长为,母线长为.在母线上的点处有一块爆米花残渣,且,一只蚂蚁从杯口的点处沿圆锥表面爬行到点,则此蚂蚁爬行的最短距离为_______.
20.如图,一个较大的圆内有15个半径为1的小圆,所有的交点都为切点,图中阴影为大圆内但在所有小圆外部分,则阴影部分的面积为___________.
三、解答题(共6个小题)
21.求阴影部分的面积.(单位:cm,结果用含π的形式表示)
22.如图,BE是⊙O的直径,点A和点D是⊙O上的两点,过点A作⊙O的切线交BE延长线于点C.
(1)若∠ADE=25°,求∠C的度数;
(2)若AC=,CE=4,求阴影部分的面积.
23.如图,如图,点A、B、C在圆O上,,直线,,点O在BD上.
(1)判断直线AD与圆O的位置关系,并说明理由;
(2)若圆的半径为6,求图中阴影部分的面积.
24.如图所示,已知圆锥底面半径,母线长为.
(1)求它的侧面展开图的圆心角;
(2)若一甲虫从A点出发沿着圆锥侧面绕行到母线的中点B,请你动脑筋想一想它所走的最短路线是多少?
25.如图,有一直径为4的圆形铁皮,要从中剪出一个最大圆心角为60°的扇形ABC.
(1)求剪下的扇形ABC(即阴影部分)的半径;
(2)若用此剪下的扇形铁皮围成一个圆锥形铁帽,求此圆锥形铁帽的底面圆的半径r.
26.已知:如图,半圆O的直径,点C,D是这个半圆的三等分点.求的度数及弦和围成的图形(图中阴影部分)的面积S.(结果保留)
参考答案:
1.A
【详解】解:设底面圆半径为r,
则,
解得r=6.
故选:A.
2.B
【详解】解:∵AB切⊙O于点B,
∴,
∵,
∴,
∵OA=4,
∴OBOA=2,
∴劣弧的长π,
故选B.
3.A
【详解】解:∵75°的圆心角所对的弧长是2.5πcm,
由弧长公式l,
∴2.5π,
解得:r=6,
故选:A.
4.B
【详解】解:由题意可知点从开始至结束所走过的路径为两个圆心角为120°,半径为1的扇形弧长,
所以点从开始至结束所走过的路径长度为:.
故选B.
5.B
【详解】解:连接OF,
∵∠AOD=45°,四边形CDEF是正方形,
∴OD=CD=DE=EF,
在Rt△OFE中,OE=2EF,
∵OF=,,
∴,
解得:EF=1,
∴EF=OD=CD=1,
∴
.
故选:B.
6.D
【详解】解:∵△ABC绕点C旋转60°得到△A′B′C,
∴△ABC≌△A′B′C,
∴, .
∵AB扫过的图形的面积=,
∴AB扫过的图形的面积=,
∴AB扫过的图形的面积=.
故选:D.
7.C
【详解】解:∵,
∴,
∴阴影部分的面积.
故选:C.
8.B
【详解】解:圆锥的侧面积为:,
故选:B.
9.A
【详解】∵,
∴圆心角的度数为n=2×30°=60°.
∴长为2π cm的弧所对的圆周角的度数为,
故选A.
10.A
【详解】解:如图:
正方形的面积;①
两个扇形的面积;②
②①,得:.
故选:A.
11. 4
【详解】解:如图,
这个圆锥的底面周长为,
设半径为r,
则有,
解得r=4;
圆锥的高是:,
侧面积为,
故答案为:4;;
12.
【详解】解:如图所示:
圆锥的侧面展开图的弧长为(cm),
∴圆锥的底面半径为(cm),
∴圆锥的高为:(cm).
故答案是:cm.
13.
【详解】解:圆锥底面是以BC为直径的圆,圆的周长是BCπ=8π,
以AB为一边,将圆锥展开,就得到一个以A为圆心,以AB为半径的扇形,弧长是l=8π,
设展开后的圆心角是n°,则,
解得:,
即展开后∠BAC=×180°=90°,
AP=AC=4,AB=8,
则在圆锥的侧面上从B点到P点的最短路线的长就是展开后线段BP的长,
由勾股定理得:,
故答案为:.
14.
【详解】解:这个圆锥的全面积(cm).
故答案为:.
15.90π
【详解】解:由图可知这个几何体是个圆锥,且它的底面圆的直径是10cm,高12cm,
则底面圆的半径是5cm,
母线长==13cm,
它的全面积=侧面积+底面积=π×5×13+π×5×5=90π(cm2).
故答案为:90π.
16.180
【详解】解:∵母线长为cm,底面半径为cm,
∴展开的扇形的弧长为,以母线为半径的圆的周长为,
∴侧面展开图扇形的圆心角=,
故答案为:.
17.3
【详解】解:连接BC,由题意知∠BAC=90°,
∴BC是⊙O的直径,BC=24cm,
∵AB=AC,
∴,
∴AB===12(cm),
∴==6π(cm)
∴圆锥的底面圆的半径=6π÷(2π)=3(cm).
故答案为:3.
18.π
【详解】解:如图,连接AC,交BD于点O,取BC的中点N,连接NH,
∴MF=BM=BNAB,
∴点F的运动轨迹为以点M为圆心,BM长为半径的圆上,
∵∠ABC=∠FBH=90°,
∴∠ABC﹣∠FBC=∠FBH﹣∠FBC,
即∠ABF=∠CBH,
∴△MBF≌△NBH(SAS),
∴NH=MF=BM=BN,
∴点H在以点N为圆心,BN长为半径的圆上,
∴当点E在C处时,点F与O重合,
当点E在B处时,点F与点B重合,
∴点H所在的圆弧的圆心角为90°,
∴点H所经过的路径长,
故答案为:π.
19.
【详解】解:,
底面周长,
将圆锥侧面沿剪开展平得一扇形,此扇形的半径,弧长等于圆锥底面圆的周长
设扇形圆心角度数为,则根据弧长公式得:
,
,
即展开图是一个半圆,
点是展开图弧的中点,
,
连接,则就是蚂蚁爬行的最短距离,
在中由勾股定理得,
,
,
即蚂蚁爬行的最短距离是.
故答案为:.
20.
【详解】解:如图,为边的高,
所有小圆相切,
,
为等边三角形,
,
,
,
,
与⊙O相切,
∴⊙O的半径,
阴影部分的面积.
故答案为:.
21.
【详解】解:如图可知,阴影部分是由以正方形四边中点为圆心,2为半径的圆的公共部分组合而成,即由8个弓形组合而成
由得:
,
∴.
22.(1)∠C=40°;
(2)阴影部分的面积为.
【详解】(1)
解:如图,连接OA,
∵AC是⊙O的切线,OA是⊙O的半径,
∴OA⊥AC,
∴∠OAC=90°,
∵∠ADE=25°,
∴∠AOE=2∠ADE=50°,
∴∠C=90°-∠AOE=90°-50°=40°;
(2)
解:设OA=OE=r,
在Rt△OAC中,由勾股定理得:,
即,
解得:r=4,
∴OC=8,
∴OA=OC,
∴∠C=30°,
∴∠AOC=60°,
∴=OA AC=×4×4=8,
∴阴影部分的面积.
23.(1)直线AD与圆O相切,理由见解析
(2)
【详解】
(1)
解:直线AD与圆O相切,理由如下:
如图,连接OA,
∵,
∴∠D=∠DBC,
∵AB=AD,
∴∠D=∠ABD,
∵,
∴∠DBC=∠ABD=∠D=30°,
∴∠BAD=120°,
∵OA=OB,
∴∠BAO=∠ABD=30°,
∴∠OAD=90°,
∴OA⊥AD,
∵OA是圆的半径,
∴直线AD与园O相切,
(2)解:如图,连接OC,作OH⊥BC于H,
∵OB=OC=6,
∴∠OCB=∠OBC=30°,
∴∠BOC=120°,
∴,
∴,
∴,
∴扇形BOC的面积为,
∵,
∴阴影部分的面积为.
24.(1);(2)
【详解】(1)解:设它的侧面展开图的圆心角为,
根据圆锥的底面周长就是侧面展开图(扇形)的弧长得:
,
又∵.
,
解得:.
∴它的侧面展开图的圆心角是90°;
(2)根据侧面展开图的圆心角是90°,画出展开图如下:
根据两点之间,线段最短可知AB为最短路径,
,B为的中点,
由(1)知
∴
∴它所走的最短路线长是.
25.(1)剪下的扇形ABC(即阴影部分)的半径为2;(2)
【详解】(1)
解:连接OA,OB,OC,作OD⊥AB于点D.
则AD=AB,
∵BA= CA,OA= OA,OB= OC,
∴△BAO≌△CAO,
∴∠BAO=∠CAO,
∵∠BAC=60°,
∴∠BAO=30 °,
∵圆的直径为4,
∴ OA=2,
∴OD=1,DA==,
∴AB=2DA=2;
∴剪下的扇形ABC(即阴影部分)的半径为2;
(2)
解:则扇形(即阴影部分)的弧长是:,
根据题意得:,
解得:r=.
答:此圆锥形铁帽的底面圆的半径为.
26.;
【详解】解:如图,连接OC、OD、CD,OC与AD交于点M,
∵点C,D是这个半圆的三等分点,
∴,
∵和为同弧所对的圆周角和圆心角,
∴,
∵,
∴和都是等边三角形,
∴,
∵在和中,
∴
∴图中阴影部分的面积等于扇形COD的面积,
∵半径
∴
一、单选题(共10个小题)
1.一个圆锥侧面展开图的扇形的弧长为,则这个圆锥底面圆的半径为( )
A.6 B.12 C.24 D.2
2.如图,AB切⊙O于点B,连接OA交⊙O于点C,连接OB.若,OA=4,则劣弧的长是( )
A.π B.π C.π D.π
3.75°的圆心角所对的弧长是2.5πcm,则此弧所在圆的半径是( )
A.6cm B.7cm C.8cm D.9cm
4.一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如图),那么B点从开始至结束所走过的路径长度为( )
A. B. C.4 D.
5.如图,在半径为,圆心角等于45°的扇形AOB内部作一个正方形CDEF,使点C在OA上,点D、E在OB上,点F在上,则阴影部分的面积为(结果保留π)( )
A. B. C. D.
6.如图,将绕点旋转得到,已知,,则线段扫过的图形面积为( )
A. B. C. D.
7.如图,△ABC内接于⊙O,若,⊙O的半径r=4,则阴影部分的面积为( )
A. B. C. D.
8.如果圆锥的母线长为5cm,底面半径为2cm,那么这个圆锥的侧面积为( )
A.10cm2 B.10cm2 C.20cm2 D.20cm2
9.在半径为6 cm的圆中,长为2π cm的弧所对的圆周角的度数为 ( )
A.30° B.45° C.60° D.90°
10.如图,正方形的边,和都是以1为半径的圆弧,则无阴影两部分的面积之差是( )
A. B. C. D.
二、填空题(共10个小题)
11.若把一个半径为12cm,圆心角为的扇形做成圆锥的侧面,则这个圆锥的底面圆的半径是_______,圆锥的高是__________,侧面积是____________.
12.用一个半径为10cm半圆纸片围成一个圆锥的侧面(接缝忽略不计),则该圆锥的高为_________.
13.如图,圆锥的轴截面是边长为8cm的正三角形ABC,P是母线AC的中点,则在圆锥的侧面上从B点到P点的最短路线的长为__________.
14.若一个圆锥的母线长为,它的半径为,则这个圆锥的全面积为________.
15.如图,是一个工件的三视图,则此工件的全面积是________cm2.
16.一个母线长为6cm,底面半径为3cm的圆锥展开后得到的侧面展开图扇形的圆心角是______度.
17.如图,从一块直径为24cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是________cm.
18.正方形的边长为4,E是边上的一个动点,在点E从点C到点B的运动过程中,小亮以B为顶点作正方形,其中点F、G都在直线上,如图.当点E到达点B时,点F、G、H与点B重合.则点H所经过的路径长为_____________.
19.如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径长为,母线长为.在母线上的点处有一块爆米花残渣,且,一只蚂蚁从杯口的点处沿圆锥表面爬行到点,则此蚂蚁爬行的最短距离为_______.
20.如图,一个较大的圆内有15个半径为1的小圆,所有的交点都为切点,图中阴影为大圆内但在所有小圆外部分,则阴影部分的面积为___________.
三、解答题(共6个小题)
21.求阴影部分的面积.(单位:cm,结果用含π的形式表示)
22.如图,BE是⊙O的直径,点A和点D是⊙O上的两点,过点A作⊙O的切线交BE延长线于点C.
(1)若∠ADE=25°,求∠C的度数;
(2)若AC=,CE=4,求阴影部分的面积.
23.如图,如图,点A、B、C在圆O上,,直线,,点O在BD上.
(1)判断直线AD与圆O的位置关系,并说明理由;
(2)若圆的半径为6,求图中阴影部分的面积.
24.如图所示,已知圆锥底面半径,母线长为.
(1)求它的侧面展开图的圆心角;
(2)若一甲虫从A点出发沿着圆锥侧面绕行到母线的中点B,请你动脑筋想一想它所走的最短路线是多少?
25.如图,有一直径为4的圆形铁皮,要从中剪出一个最大圆心角为60°的扇形ABC.
(1)求剪下的扇形ABC(即阴影部分)的半径;
(2)若用此剪下的扇形铁皮围成一个圆锥形铁帽,求此圆锥形铁帽的底面圆的半径r.
26.已知:如图,半圆O的直径,点C,D是这个半圆的三等分点.求的度数及弦和围成的图形(图中阴影部分)的面积S.(结果保留)
参考答案:
1.A
【详解】解:设底面圆半径为r,
则,
解得r=6.
故选:A.
2.B
【详解】解:∵AB切⊙O于点B,
∴,
∵,
∴,
∵OA=4,
∴OBOA=2,
∴劣弧的长π,
故选B.
3.A
【详解】解:∵75°的圆心角所对的弧长是2.5πcm,
由弧长公式l,
∴2.5π,
解得:r=6,
故选:A.
4.B
【详解】解:由题意可知点从开始至结束所走过的路径为两个圆心角为120°,半径为1的扇形弧长,
所以点从开始至结束所走过的路径长度为:.
故选B.
5.B
【详解】解:连接OF,
∵∠AOD=45°,四边形CDEF是正方形,
∴OD=CD=DE=EF,
在Rt△OFE中,OE=2EF,
∵OF=,,
∴,
解得:EF=1,
∴EF=OD=CD=1,
∴
.
故选:B.
6.D
【详解】解:∵△ABC绕点C旋转60°得到△A′B′C,
∴△ABC≌△A′B′C,
∴, .
∵AB扫过的图形的面积=,
∴AB扫过的图形的面积=,
∴AB扫过的图形的面积=.
故选:D.
7.C
【详解】解:∵,
∴,
∴阴影部分的面积.
故选:C.
8.B
【详解】解:圆锥的侧面积为:,
故选:B.
9.A
【详解】∵,
∴圆心角的度数为n=2×30°=60°.
∴长为2π cm的弧所对的圆周角的度数为,
故选A.
10.A
【详解】解:如图:
正方形的面积;①
两个扇形的面积;②
②①,得:.
故选:A.
11. 4
【详解】解:如图,
这个圆锥的底面周长为,
设半径为r,
则有,
解得r=4;
圆锥的高是:,
侧面积为,
故答案为:4;;
12.
【详解】解:如图所示:
圆锥的侧面展开图的弧长为(cm),
∴圆锥的底面半径为(cm),
∴圆锥的高为:(cm).
故答案是:cm.
13.
【详解】解:圆锥底面是以BC为直径的圆,圆的周长是BCπ=8π,
以AB为一边,将圆锥展开,就得到一个以A为圆心,以AB为半径的扇形,弧长是l=8π,
设展开后的圆心角是n°,则,
解得:,
即展开后∠BAC=×180°=90°,
AP=AC=4,AB=8,
则在圆锥的侧面上从B点到P点的最短路线的长就是展开后线段BP的长,
由勾股定理得:,
故答案为:.
14.
【详解】解:这个圆锥的全面积(cm).
故答案为:.
15.90π
【详解】解:由图可知这个几何体是个圆锥,且它的底面圆的直径是10cm,高12cm,
则底面圆的半径是5cm,
母线长==13cm,
它的全面积=侧面积+底面积=π×5×13+π×5×5=90π(cm2).
故答案为:90π.
16.180
【详解】解:∵母线长为cm,底面半径为cm,
∴展开的扇形的弧长为,以母线为半径的圆的周长为,
∴侧面展开图扇形的圆心角=,
故答案为:.
17.3
【详解】解:连接BC,由题意知∠BAC=90°,
∴BC是⊙O的直径,BC=24cm,
∵AB=AC,
∴,
∴AB===12(cm),
∴==6π(cm)
∴圆锥的底面圆的半径=6π÷(2π)=3(cm).
故答案为:3.
18.π
【详解】解:如图,连接AC,交BD于点O,取BC的中点N,连接NH,
∴MF=BM=BNAB,
∴点F的运动轨迹为以点M为圆心,BM长为半径的圆上,
∵∠ABC=∠FBH=90°,
∴∠ABC﹣∠FBC=∠FBH﹣∠FBC,
即∠ABF=∠CBH,
∴△MBF≌△NBH(SAS),
∴NH=MF=BM=BN,
∴点H在以点N为圆心,BN长为半径的圆上,
∴当点E在C处时,点F与O重合,
当点E在B处时,点F与点B重合,
∴点H所在的圆弧的圆心角为90°,
∴点H所经过的路径长,
故答案为:π.
19.
【详解】解:,
底面周长,
将圆锥侧面沿剪开展平得一扇形,此扇形的半径,弧长等于圆锥底面圆的周长
设扇形圆心角度数为,则根据弧长公式得:
,
,
即展开图是一个半圆,
点是展开图弧的中点,
,
连接,则就是蚂蚁爬行的最短距离,
在中由勾股定理得,
,
,
即蚂蚁爬行的最短距离是.
故答案为:.
20.
【详解】解:如图,为边的高,
所有小圆相切,
,
为等边三角形,
,
,
,
,
与⊙O相切,
∴⊙O的半径,
阴影部分的面积.
故答案为:.
21.
【详解】解:如图可知,阴影部分是由以正方形四边中点为圆心,2为半径的圆的公共部分组合而成,即由8个弓形组合而成
由得:
,
∴.
22.(1)∠C=40°;
(2)阴影部分的面积为.
【详解】(1)
解:如图,连接OA,
∵AC是⊙O的切线,OA是⊙O的半径,
∴OA⊥AC,
∴∠OAC=90°,
∵∠ADE=25°,
∴∠AOE=2∠ADE=50°,
∴∠C=90°-∠AOE=90°-50°=40°;
(2)
解:设OA=OE=r,
在Rt△OAC中,由勾股定理得:,
即,
解得:r=4,
∴OC=8,
∴OA=OC,
∴∠C=30°,
∴∠AOC=60°,
∴=OA AC=×4×4=8,
∴阴影部分的面积.
23.(1)直线AD与圆O相切,理由见解析
(2)
【详解】
(1)
解:直线AD与圆O相切,理由如下:
如图,连接OA,
∵,
∴∠D=∠DBC,
∵AB=AD,
∴∠D=∠ABD,
∵,
∴∠DBC=∠ABD=∠D=30°,
∴∠BAD=120°,
∵OA=OB,
∴∠BAO=∠ABD=30°,
∴∠OAD=90°,
∴OA⊥AD,
∵OA是圆的半径,
∴直线AD与园O相切,
(2)解:如图,连接OC,作OH⊥BC于H,
∵OB=OC=6,
∴∠OCB=∠OBC=30°,
∴∠BOC=120°,
∴,
∴,
∴,
∴扇形BOC的面积为,
∵,
∴阴影部分的面积为.
24.(1);(2)
【详解】(1)解:设它的侧面展开图的圆心角为,
根据圆锥的底面周长就是侧面展开图(扇形)的弧长得:
,
又∵.
,
解得:.
∴它的侧面展开图的圆心角是90°;
(2)根据侧面展开图的圆心角是90°,画出展开图如下:
根据两点之间,线段最短可知AB为最短路径,
,B为的中点,
由(1)知
∴
∴它所走的最短路线长是.
25.(1)剪下的扇形ABC(即阴影部分)的半径为2;(2)
【详解】(1)
解:连接OA,OB,OC,作OD⊥AB于点D.
则AD=AB,
∵BA= CA,OA= OA,OB= OC,
∴△BAO≌△CAO,
∴∠BAO=∠CAO,
∵∠BAC=60°,
∴∠BAO=30 °,
∵圆的直径为4,
∴ OA=2,
∴OD=1,DA==,
∴AB=2DA=2;
∴剪下的扇形ABC(即阴影部分)的半径为2;
(2)
解:则扇形(即阴影部分)的弧长是:,
根据题意得:,
解得:r=.
答:此圆锥形铁帽的底面圆的半径为.
26.;
【详解】解:如图,连接OC、OD、CD,OC与AD交于点M,
∵点C,D是这个半圆的三等分点,
∴,
∵和为同弧所对的圆周角和圆心角,
∴,
∵,
∴和都是等边三角形,
∴,
∵在和中,
∴
∴图中阴影部分的面积等于扇形COD的面积,
∵半径
∴
同课章节目录
