10.3 实数 第一课课件[下学期]
文档属性
| 名称 | 10.3 实数 第一课课件[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 709.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-06-05 00:00:00 | ||
图片预览









文档简介
课件31张PPT。10.3实数
使用计算器计算,把下列有理数写成小数的形式,你有什么发现?探究 事实上,任何一个有理数都可以写成有限小数或无限循环小数。 反过来,任何有限小数或无限循环小数也都是有理数除了有限小数和无限循环小数,还有什么其它类型的小数吗?1.圆周率2.开不尽的方根3.人为构造的数 无限不循环的小数
----------叫做无理数 无限不循环的小数 ----------叫做无理数 无限不循环的小数 ---------- 叫做无理数.学习新知(1) 你能举出一些无理数吗?试一试每个有理数都可以用数轴上的点表示,那么无理数
是否也可以用数轴上的点来表示呢? 你能在数轴上找到表示 这样的无理数的
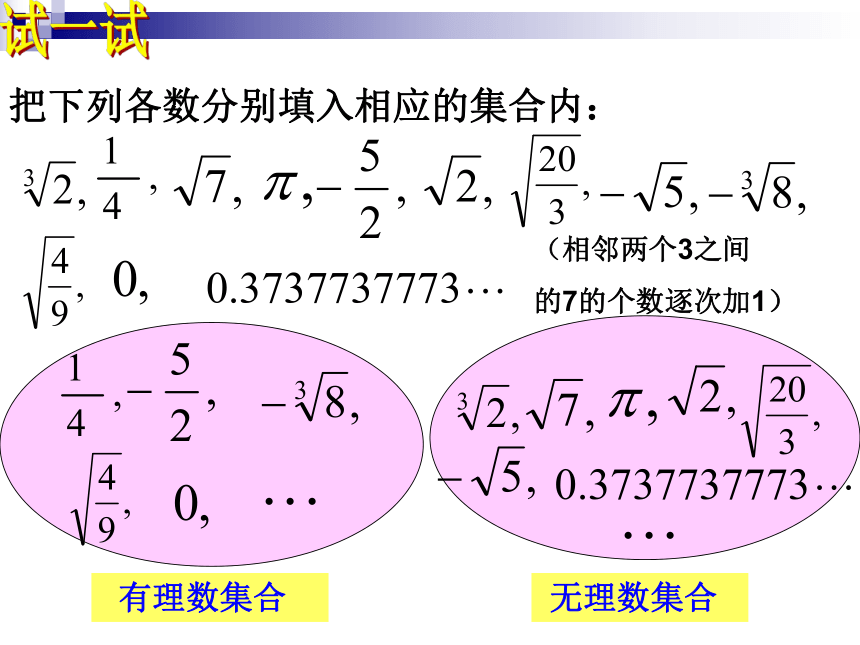
点吗?你能举出一些无理数吗?试一试 有理数集合 无理数集合有理数和无理数统称
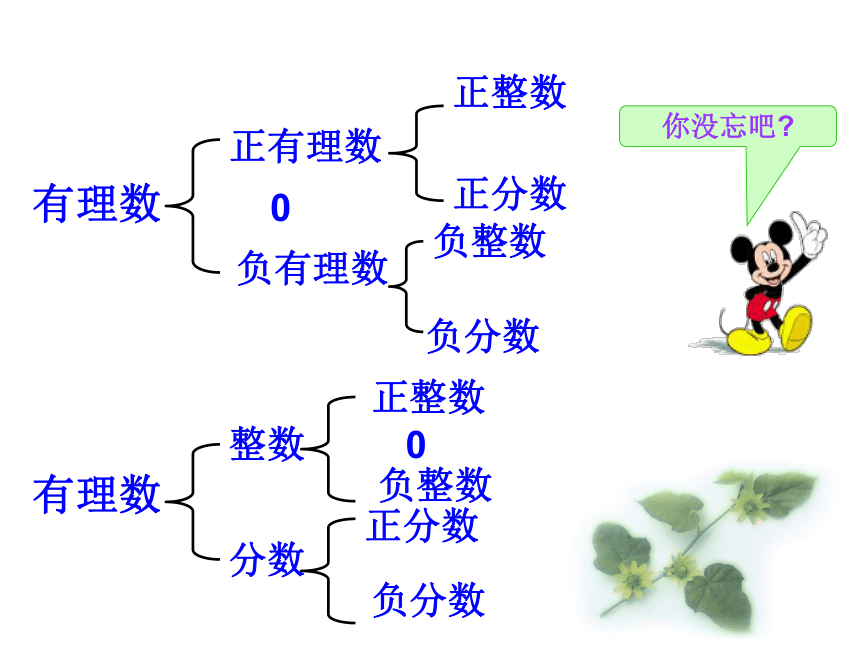
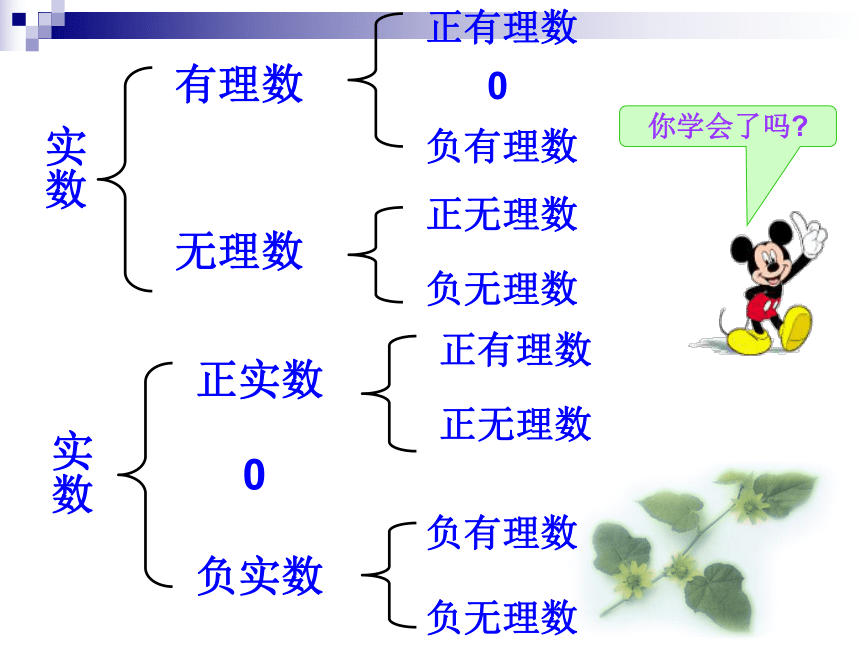
实数有理数正有理数负有理数 0你没忘吧?有理数正分数正整数负整数负分数分数整数正整数 0负整数正分数负分数实数实数有理数无理数正有理数负有理数 0正无理数负无理数正实数 0负实数正有理数正无理数负有理数负无理数你学会了吗?练一练把下列各数填入相应的集合内:(1)有理数集合:(2)无理数集合:(3)整数集合:(4)负数集合:(5)分数集合:(6)实数集合:一、判断:1.实数不是有理数就是无理数。( )2.无理数都是无限不循环小数。( )3.无理数都是无限小数。( )4.带根号的数都是无理数。( )5.无理数一定都带根号。( )6.两个无理数之积不一定是无理数。( )7.两个无理数之和一定是无理数。( )×××在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。二、填空5、在实数 中,
整数有
有理数有
无理数有
实数有它本身0它的相反数有理数能不能将数轴排满?直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O,,点O,的坐标是多少? 实数与数轴上的点一一对应。即每一个实数都可以用数轴上的一个点来表示;反之数轴上的每一点都表示一个实数。平面直角坐标系内的点与有序实数对是一一对应的。0-1121AB 如图:OA=OB,数轴上A点对应的数是什么? 如果将所有有理数都标到数轴上,那么数轴被填满了吗?探索 & 交流在数轴上作出 的对应点.0123-112012-1-2A一个实数a 每个实数都可以用数轴上的
一个点来表示;反过来,数轴上的每一个点都表示一个实数.即实数和数轴上点是一一对应的. 同样,在数轴上,右边的点表示的数比左边的点表示的数大.数轴上一个点有一个实数有一个实数数轴上一个点实数与数轴上的点一一对应.在数轴上表示出下列各数,并比较它们的大小(用“<”号连接)
合作学习请同学们总结有理数的运算律和运算法则1.交换律 : 加法 a+b=b+a
乘法a×b=b×a2.结合律: 加法(a+b)+c=a+(b+c)
乘法(a×b)×c=a×(b×c)3.分配律: a× (b+c)= a×b+ a×c注:有理数的运算律和运算法则在实数范围内同样适用实数的运算顺序 先算乘方和开方,再算乘除,最后算加减。如果遇到括号, 则先进行括号里的运算典型例题解:(1) = 0.748343301≈0.748(2) =
=
=-2.464101615≈-2.464 计算:
(1) (精确到0.01)
(2) (结果保留3各有效数字)
(3) ( 精确到0.01)典型例题例2:计算解:原式=
=18.94427191≈18.94===计算:
(1) (结果保留3个有效数字)
(2) (精确到0.01)
(3) (结果保留4个有效数字)计算下面的式子:
与
与
你发现了什么?换几个数再试一试,是否有相同的规律?探究活动实数有理数无理数分数整数正整数 0负整数正分数负分数自然数正无理数负无理数无限不循环小数有限小数及无限循环小数一般有三种情况
使用计算器计算,把下列有理数写成小数的形式,你有什么发现?探究 事实上,任何一个有理数都可以写成有限小数或无限循环小数。 反过来,任何有限小数或无限循环小数也都是有理数除了有限小数和无限循环小数,还有什么其它类型的小数吗?1.圆周率2.开不尽的方根3.人为构造的数 无限不循环的小数
----------叫做无理数 无限不循环的小数 ----------叫做无理数 无限不循环的小数 ---------- 叫做无理数.学习新知(1) 你能举出一些无理数吗?试一试每个有理数都可以用数轴上的点表示,那么无理数
是否也可以用数轴上的点来表示呢? 你能在数轴上找到表示 这样的无理数的
点吗?你能举出一些无理数吗?试一试 有理数集合 无理数集合有理数和无理数统称
实数有理数正有理数负有理数 0你没忘吧?有理数正分数正整数负整数负分数分数整数正整数 0负整数正分数负分数实数实数有理数无理数正有理数负有理数 0正无理数负无理数正实数 0负实数正有理数正无理数负有理数负无理数你学会了吗?练一练把下列各数填入相应的集合内:(1)有理数集合:(2)无理数集合:(3)整数集合:(4)负数集合:(5)分数集合:(6)实数集合:一、判断:1.实数不是有理数就是无理数。( )2.无理数都是无限不循环小数。( )3.无理数都是无限小数。( )4.带根号的数都是无理数。( )5.无理数一定都带根号。( )6.两个无理数之积不一定是无理数。( )7.两个无理数之和一定是无理数。( )×××在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。二、填空5、在实数 中,
整数有
有理数有
无理数有
实数有它本身0它的相反数有理数能不能将数轴排满?直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O,,点O,的坐标是多少? 实数与数轴上的点一一对应。即每一个实数都可以用数轴上的一个点来表示;反之数轴上的每一点都表示一个实数。平面直角坐标系内的点与有序实数对是一一对应的。0-1121AB 如图:OA=OB,数轴上A点对应的数是什么? 如果将所有有理数都标到数轴上,那么数轴被填满了吗?探索 & 交流在数轴上作出 的对应点.0123-112012-1-2A一个实数a 每个实数都可以用数轴上的
一个点来表示;反过来,数轴上的每一个点都表示一个实数.即实数和数轴上点是一一对应的. 同样,在数轴上,右边的点表示的数比左边的点表示的数大.数轴上一个点有一个实数有一个实数数轴上一个点实数与数轴上的点一一对应.在数轴上表示出下列各数,并比较它们的大小(用“<”号连接)
合作学习请同学们总结有理数的运算律和运算法则1.交换律 : 加法 a+b=b+a
乘法a×b=b×a2.结合律: 加法(a+b)+c=a+(b+c)
乘法(a×b)×c=a×(b×c)3.分配律: a× (b+c)= a×b+ a×c注:有理数的运算律和运算法则在实数范围内同样适用实数的运算顺序 先算乘方和开方,再算乘除,最后算加减。如果遇到括号, 则先进行括号里的运算典型例题解:(1) = 0.748343301≈0.748(2) =
=
=-2.464101615≈-2.464 计算:
(1) (精确到0.01)
(2) (结果保留3各有效数字)
(3) ( 精确到0.01)典型例题例2:计算解:原式=
=18.94427191≈18.94===计算:
(1) (结果保留3个有效数字)
(2) (精确到0.01)
(3) (结果保留4个有效数字)计算下面的式子:
与
与
你发现了什么?换几个数再试一试,是否有相同的规律?探究活动实数有理数无理数分数整数正整数 0负整数正分数负分数自然数正无理数负无理数无限不循环小数有限小数及无限循环小数一般有三种情况
