华师大版数学七年级上册 4.6.2 角的比较和运算 课件(共29张PPT)
文档属性
| 名称 | 华师大版数学七年级上册 4.6.2 角的比较和运算 课件(共29张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-14 09:26:57 | ||
图片预览






文档简介
(共29张PPT)
第4章 图形的初步认识
4.6 角
第2课时 角的比较和运算
1
课堂讲解
角的比较、角的运算、角的平分线
2
课时流程
逐点
导讲练
课堂小结
作业提升
观察如图所示的三个角,哪一个最大?
你能从比较线
段长短的方法
得到启示吗?
1
知识点
角的比较
知1-讲
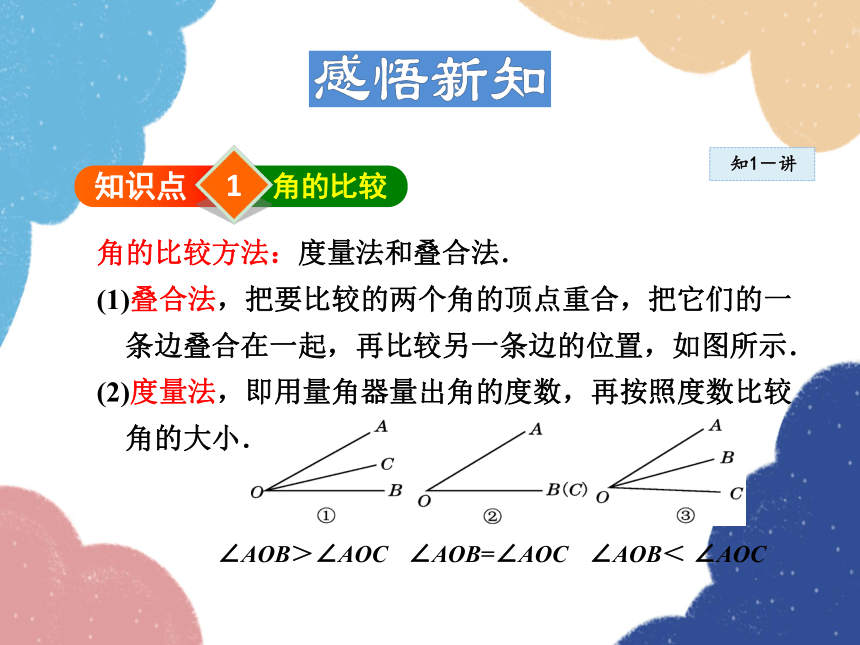
角的比较方法:度量法和叠合法.
(1)叠合法,把要比较的两个角的顶点重合,把它们的一
条边叠合在一起,再比较另一条边的位置,如图所示.
(2)度量法,即用量角器量出角的度数,再按照度数比较
角的大小.
∠AOB>∠AOC
∠AOB=∠AOC
∠AOB< ∠AOC
知识点
知1-讲
【例1】 根据图,回答下列问题:
(1)比较∠FOD与∠FOE的大小;
(2)借助三角尺比较∠DOE 与∠DOF 的大小.
导引:(1)中两个角有重合边和重合顶点,利用叠合法
比较一目了然,因为OD 边在∠ FOE的内
部,所以有∠FOD <∠FOE.
(2)∠DOE明显大于 45°,而∠DOF 明显小于
45°,故有∠ DOE >∠DOF .
解: (1)∠FOD<∠FOE.
(2)用含有45°角的三角尺比较,可得∠DOE>
45°,∠DOF<45°,所以∠DOE>∠DOF.
总 结
知1-讲
用叠合法比较角的大小时,一定要将两个角的另一
边落在重合边的同侧.有一边重合且另一边在重合边的
同侧的两角,通过观察法就可以比较大小;两边都不重
合,或有一边重合但另一边在重合边的异侧的两角,可
通过度量法比较大小 .
1
知1-练
(来自教材)
先观察下列各组角,其中哪一个角较大?然后用量
角器量一量每个角,看看你的观察结果是否正确.
2
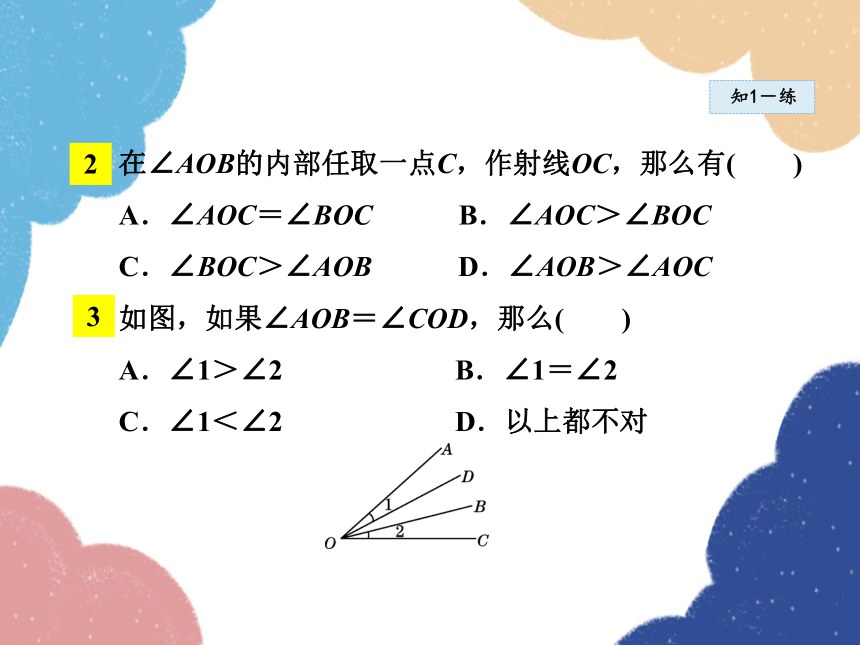
在∠AOB的内部任取一点C,作射线OC,那么有( )
A.∠AOC=∠BOC B.∠AOC>∠BOC
C.∠BOC>∠AOB D.∠AOB>∠AOC
如图,如果∠AOB=∠COD,那么( )
A.∠1>∠2 B.∠1=∠2
C.∠1<∠2 D.以上都不对
知1-练
3
2
知识点
角的运算
知2-导
一副三角尺上的角是一些常用的角,除了可以用
它们直接画出30°、45°、60°和90°的角之外,还可
以画出其他一些特殊的角.如图所示,用两种方法放置一
副三角尺,可以画出75°和15°的角.
想一想 用一副三角尺还可以画出哪些特殊的角?
知识点
知2-导
做一做
如图,∠AOB为已知角,试按下列步骤用圆规和直尺准
确地画一个角等于∠AOB.
第一步:画射线O′A′;
第二步:以点O为圆心,
以适当长为半径画弧,交OA于点C,交OB于点D;
知识点
知2-导
第三步:以点O′为圆心,以OC长为半径画弧,交O′A′
于点C′;
第四步:以点C′为圆心,以CD长为半径画弧,交前一条
弧于点D ′;
第五步:经过点D′画射线O′B′. ∠ A′ O′B′ 就是所
要画的角.
知识点
知2-讲
【例2】用一副三角尺不能全部画出的一组角的度
数是( )
A.15°、30°、45°
B.45°、60°、75°
C.90°、105°、120°
D.100°、135°、150°
D
知识点
知2-讲
导引:用三角尺可直接画出30°、45°、60°、90°的
角,再用45°和30°的角叠加就画出了75°的
角;同理可画出15°、105°、120°、135°、
150°、165°的角.因为无法用三角尺中角的度
数拼出100°,所以不能画出的角的度数是100°.
总 结
知2-讲
用三角尺直接画特殊角的步骤:先画一条射线,再
把三角尺所画角的一边与射线重合,顶点与射线端点重
合,最后沿另一边画一条射线,标出角的度数.
知识点
知2-讲
【例3】 如图,∠AOB=48°,∠1=32°24′,求
∠2的度数.
导引: 要求∠2的度数,就是要把它转化为用已知角的
关系式来表示.根据图形可知,∠1+∠2=
∠AOB,因此∠2=∠AOB-∠1.
解: 因为∠AOB=48°,∠1=32°24′,
所以∠2=48°-32°24′=47°60′-
32°24′=15°36′.
总 结
知2-讲
解题的基本方法是从图形中找出等量关系:
∠2=∠AOB-∠1,结合角度的运算求得∠2
的度数,体现了数形结合思想.
1
知2-练
若一个60°的角绕顶点旋转15°,则重叠部分的角的大小是( )
A.15° B.30° C.45° D.75°
如图,∠AOD-∠AOC=( )
A.∠AOC B.∠BOC C.∠BOD D.∠COD
2
3
知2-练
(中考·滨州)借助一副三角尺,你能画出下面哪个度数的角( )
A.65° B.75° C.85° D.95°
(中考·辽宁)如图,已知直线AB,CD相交于点O,
OA平分∠EOC,∠EOC=110°,
则∠BOD的度数是( )
A.25° B.35° C.45° D.55°
4
3
知识点
角的平分线
知3-导
做一做
如图,用量角器和直尺在纸上画∠AOB=84°.
然后沿点O对折,使边OB和OA重合,那么折
痕把角分成了大小相等的两部分.
你也可以用量角器画出等分∠AOB的射线OC.
知识点
知3-讲
定义:从一个角的顶点引出的一条射线,把这个角
分成两个相等的角,这条射线叫做这个角的平分线.
知识点
知3-讲
【例4】 如图,∠1=∠2,∠3=∠4,则下列结论:①
AD平分∠BAF;②AF平分∠DAC;③AE平分
∠DAF;④AF平分∠BAC;⑤AE平分∠BAC,
其中正确的有( )
A.4个 B.3个 C.2个 D.1个
导引: 由角的平分线的几何表示可知:当∠1=∠2时,
AE平分∠DAF;再由∠3=∠4可得∠1+∠3=∠2
+∠4,即∠BAE=∠CAE,因此AE平分∠BAC.
C
总 结
知3-讲
判断一条射线是不是角的平分线,只要看这条射
线是否将角分成相等的两个角.
知识点
知3-讲
【例5】 如图,OC是∠AOD的平分线,
OE是∠BOD的平分线.
(1)如果∠AOB=130°,那么∠COE是多少度?
(2)在(1)的条件下,如果∠DOC=20°,那么
∠BOE是多少度?
导引: (1)由已知可知∠DOC= ∠AOD,∠DOE= ∠BOD.
由于∠COE=∠DOC+∠DOE,因此,∠COE=
∠AOD+ ∠BOD= ∠AOB.
(2)结合(1)的结论可求出∠DOE的度数,从而求出
∠BOE的度数.
知识点
知3-讲
解:(1)因为OC平分∠AOD,所以∠DOC= ∠AOD.
因为OE平分∠BOD,所以∠DOE= ∠BOD.
所以∠COE=∠DOC+∠DOE= (∠AOD+∠BOD)
= ∠AOB= ×130°=65°.
(2)由(1)可知∠COE=65°,因为∠DOC=20°,
所以∠DOE=∠COE-∠DOC=45°.
因为OE平分∠BOD,
所以∠BOE=∠DOE=45°.
总 结
知3-讲
1.利用角平分线进行计算时,要灵活运用角平分线的
几种不同表达方式.
2.在计算角的大小时,常常要用到等量代换,用已知
角代替与它相等的未知角.
1
知3-练
如图,∠AOB=55°.画出∠BOC的平分线OD,并计算
∠AOD的度数.
(来自教材)
如图所示,若有∠BAD=∠CAD,∠BCE=∠ACE,
则下列结论中错误的是( )
A.AD是∠BAC的平分线 B.CE是∠ACD的平分线
C.∠BCE= ∠ACB D.CE是∠ABC的平分线
2
3
知3-练
(中考·大连)如图,点O在直线AB上,射线OC平分∠BOD,若∠COB=35°,则∠AOD等于( )
A.35° B.70° C.110° D.145°
4
(2014·滨州)如图,OB是∠AOC的平分线,OD是
∠COE的平分线,如果∠AOB=40°,∠COE=60°,
则∠BOD的度数为( )
A.50° B.60° C.65° D.70°
1、角的比较方法:度量法和叠合法
2、角的运算
3、角的平分线 :
要点精析:
(1)角平分线是在角的内部从角的顶点引出的一条射线,
不是直线或线段;
(2)角平分线把角分成了两个相等的角.
第4章 图形的初步认识
4.6 角
第2课时 角的比较和运算
1
课堂讲解
角的比较、角的运算、角的平分线
2
课时流程
逐点
导讲练
课堂小结
作业提升
观察如图所示的三个角,哪一个最大?
你能从比较线
段长短的方法
得到启示吗?
1
知识点
角的比较
知1-讲
角的比较方法:度量法和叠合法.
(1)叠合法,把要比较的两个角的顶点重合,把它们的一
条边叠合在一起,再比较另一条边的位置,如图所示.
(2)度量法,即用量角器量出角的度数,再按照度数比较
角的大小.
∠AOB>∠AOC
∠AOB=∠AOC
∠AOB< ∠AOC
知识点
知1-讲
【例1】 根据图,回答下列问题:
(1)比较∠FOD与∠FOE的大小;
(2)借助三角尺比较∠DOE 与∠DOF 的大小.
导引:(1)中两个角有重合边和重合顶点,利用叠合法
比较一目了然,因为OD 边在∠ FOE的内
部,所以有∠FOD <∠FOE.
(2)∠DOE明显大于 45°,而∠DOF 明显小于
45°,故有∠ DOE >∠DOF .
解: (1)∠FOD<∠FOE.
(2)用含有45°角的三角尺比较,可得∠DOE>
45°,∠DOF<45°,所以∠DOE>∠DOF.
总 结
知1-讲
用叠合法比较角的大小时,一定要将两个角的另一
边落在重合边的同侧.有一边重合且另一边在重合边的
同侧的两角,通过观察法就可以比较大小;两边都不重
合,或有一边重合但另一边在重合边的异侧的两角,可
通过度量法比较大小 .
1
知1-练
(来自教材)
先观察下列各组角,其中哪一个角较大?然后用量
角器量一量每个角,看看你的观察结果是否正确.
2
在∠AOB的内部任取一点C,作射线OC,那么有( )
A.∠AOC=∠BOC B.∠AOC>∠BOC
C.∠BOC>∠AOB D.∠AOB>∠AOC
如图,如果∠AOB=∠COD,那么( )
A.∠1>∠2 B.∠1=∠2
C.∠1<∠2 D.以上都不对
知1-练
3
2
知识点
角的运算
知2-导
一副三角尺上的角是一些常用的角,除了可以用
它们直接画出30°、45°、60°和90°的角之外,还可
以画出其他一些特殊的角.如图所示,用两种方法放置一
副三角尺,可以画出75°和15°的角.
想一想 用一副三角尺还可以画出哪些特殊的角?
知识点
知2-导
做一做
如图,∠AOB为已知角,试按下列步骤用圆规和直尺准
确地画一个角等于∠AOB.
第一步:画射线O′A′;
第二步:以点O为圆心,
以适当长为半径画弧,交OA于点C,交OB于点D;
知识点
知2-导
第三步:以点O′为圆心,以OC长为半径画弧,交O′A′
于点C′;
第四步:以点C′为圆心,以CD长为半径画弧,交前一条
弧于点D ′;
第五步:经过点D′画射线O′B′. ∠ A′ O′B′ 就是所
要画的角.
知识点
知2-讲
【例2】用一副三角尺不能全部画出的一组角的度
数是( )
A.15°、30°、45°
B.45°、60°、75°
C.90°、105°、120°
D.100°、135°、150°
D
知识点
知2-讲
导引:用三角尺可直接画出30°、45°、60°、90°的
角,再用45°和30°的角叠加就画出了75°的
角;同理可画出15°、105°、120°、135°、
150°、165°的角.因为无法用三角尺中角的度
数拼出100°,所以不能画出的角的度数是100°.
总 结
知2-讲
用三角尺直接画特殊角的步骤:先画一条射线,再
把三角尺所画角的一边与射线重合,顶点与射线端点重
合,最后沿另一边画一条射线,标出角的度数.
知识点
知2-讲
【例3】 如图,∠AOB=48°,∠1=32°24′,求
∠2的度数.
导引: 要求∠2的度数,就是要把它转化为用已知角的
关系式来表示.根据图形可知,∠1+∠2=
∠AOB,因此∠2=∠AOB-∠1.
解: 因为∠AOB=48°,∠1=32°24′,
所以∠2=48°-32°24′=47°60′-
32°24′=15°36′.
总 结
知2-讲
解题的基本方法是从图形中找出等量关系:
∠2=∠AOB-∠1,结合角度的运算求得∠2
的度数,体现了数形结合思想.
1
知2-练
若一个60°的角绕顶点旋转15°,则重叠部分的角的大小是( )
A.15° B.30° C.45° D.75°
如图,∠AOD-∠AOC=( )
A.∠AOC B.∠BOC C.∠BOD D.∠COD
2
3
知2-练
(中考·滨州)借助一副三角尺,你能画出下面哪个度数的角( )
A.65° B.75° C.85° D.95°
(中考·辽宁)如图,已知直线AB,CD相交于点O,
OA平分∠EOC,∠EOC=110°,
则∠BOD的度数是( )
A.25° B.35° C.45° D.55°
4
3
知识点
角的平分线
知3-导
做一做
如图,用量角器和直尺在纸上画∠AOB=84°.
然后沿点O对折,使边OB和OA重合,那么折
痕把角分成了大小相等的两部分.
你也可以用量角器画出等分∠AOB的射线OC.
知识点
知3-讲
定义:从一个角的顶点引出的一条射线,把这个角
分成两个相等的角,这条射线叫做这个角的平分线.
知识点
知3-讲
【例4】 如图,∠1=∠2,∠3=∠4,则下列结论:①
AD平分∠BAF;②AF平分∠DAC;③AE平分
∠DAF;④AF平分∠BAC;⑤AE平分∠BAC,
其中正确的有( )
A.4个 B.3个 C.2个 D.1个
导引: 由角的平分线的几何表示可知:当∠1=∠2时,
AE平分∠DAF;再由∠3=∠4可得∠1+∠3=∠2
+∠4,即∠BAE=∠CAE,因此AE平分∠BAC.
C
总 结
知3-讲
判断一条射线是不是角的平分线,只要看这条射
线是否将角分成相等的两个角.
知识点
知3-讲
【例5】 如图,OC是∠AOD的平分线,
OE是∠BOD的平分线.
(1)如果∠AOB=130°,那么∠COE是多少度?
(2)在(1)的条件下,如果∠DOC=20°,那么
∠BOE是多少度?
导引: (1)由已知可知∠DOC= ∠AOD,∠DOE= ∠BOD.
由于∠COE=∠DOC+∠DOE,因此,∠COE=
∠AOD+ ∠BOD= ∠AOB.
(2)结合(1)的结论可求出∠DOE的度数,从而求出
∠BOE的度数.
知识点
知3-讲
解:(1)因为OC平分∠AOD,所以∠DOC= ∠AOD.
因为OE平分∠BOD,所以∠DOE= ∠BOD.
所以∠COE=∠DOC+∠DOE= (∠AOD+∠BOD)
= ∠AOB= ×130°=65°.
(2)由(1)可知∠COE=65°,因为∠DOC=20°,
所以∠DOE=∠COE-∠DOC=45°.
因为OE平分∠BOD,
所以∠BOE=∠DOE=45°.
总 结
知3-讲
1.利用角平分线进行计算时,要灵活运用角平分线的
几种不同表达方式.
2.在计算角的大小时,常常要用到等量代换,用已知
角代替与它相等的未知角.
1
知3-练
如图,∠AOB=55°.画出∠BOC的平分线OD,并计算
∠AOD的度数.
(来自教材)
如图所示,若有∠BAD=∠CAD,∠BCE=∠ACE,
则下列结论中错误的是( )
A.AD是∠BAC的平分线 B.CE是∠ACD的平分线
C.∠BCE= ∠ACB D.CE是∠ABC的平分线
2
3
知3-练
(中考·大连)如图,点O在直线AB上,射线OC平分∠BOD,若∠COB=35°,则∠AOD等于( )
A.35° B.70° C.110° D.145°
4
(2014·滨州)如图,OB是∠AOC的平分线,OD是
∠COE的平分线,如果∠AOB=40°,∠COE=60°,
则∠BOD的度数为( )
A.50° B.60° C.65° D.70°
1、角的比较方法:度量法和叠合法
2、角的运算
3、角的平分线 :
要点精析:
(1)角平分线是在角的内部从角的顶点引出的一条射线,
不是直线或线段;
(2)角平分线把角分成了两个相等的角.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
