实数1[下学期]
图片预览








文档简介
课件23张PPT。§ 10。3 实 数
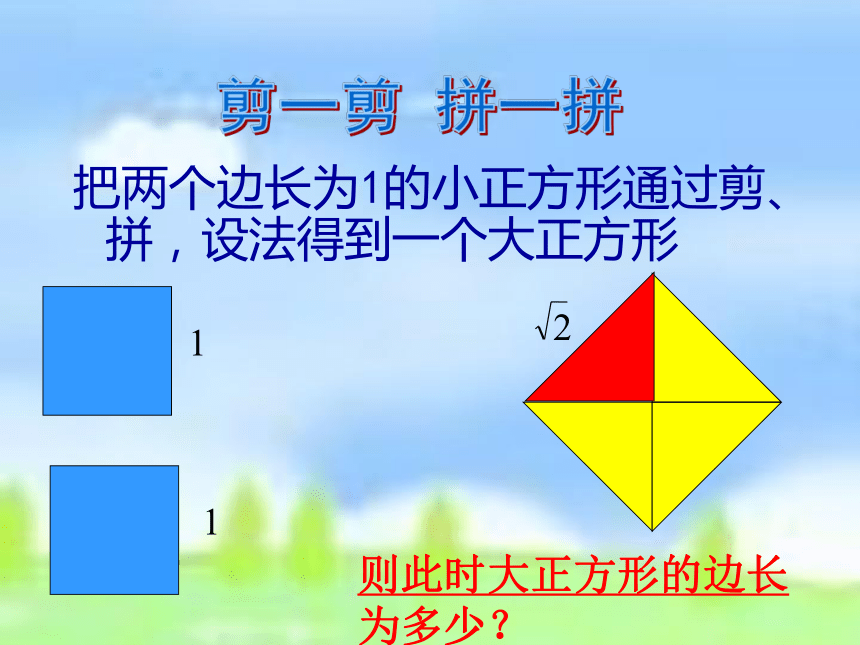
(1)若正方形的边长是6,则它的面积是 (2)若正方形的边长是a,则它的面积是 (3)若正方形的面积是25,则它的边长是(4)若正方形的面积是2,则它的边长是 365把两个边长为1的小正方形通过剪、拼,设法得到一个大正方形剪一剪 拼一拼11则此时大正方形的边长为多少? 是不是有理数? 把下列各有理数数写成小数的形式,你有什么 发现?探究有理数的特征 事实上,任何一个有理数都可以写成有限小数或 无限且循环小数。1.414 213 562 373 095 048 801 688 724 209 6……我们把这种_____________叫做无理数。是不是整数?是不是分数?由计算机可得无限不循环小数不是不是≈
例如:圆周率 及一些含有 的数是否无理数?是 理由:______无限不循环小数
像 的数是否为无理数?
是
理由:______无限不循环小数哪?有一定的规律,但不循环的无限小数都是无理数。0.1010010001…
—234.232232223…
0.12345678910111213 …〔两个3之间依次多1个2〕〔小数部分有相继的正整数组成〕〔两个1之间依次多1个0〕观察A 有理数B无理数练习、判断下列数哪些是有理数?哪些是无理数? 有理数是:
无理数是:
, , , ,有理数和无理数统称为实数。(无限不循环小数)(有限小数和无限循环小数)由于不是0的有理数和无理数都有正负之分
则实数也可以这样分类
把数从有理数扩充到实数以后,有理数的相反数和绝对值的概念同样适用于实数。因为
所以绝对值等于 的数是 和
例如:已知一个数的绝对值是 ,求这个数
解:
(1) 的相反数是__________
(2) 的相反数是
(3) ___________
(4)绝对值等于 的数是 _________ 试一试结论实数a的相反数是______
一个正数的绝对值是它______
一个负数的绝对值是它的_______
0的绝对值还是_________-a本身相反数0OO′的长是这个圆的周长 ,所以点O′的坐标是问题:每个有理数都可以用数轴上的点来表示.
无理数是否也可以用数轴上的点来表示出来呢?无理数 可以用数轴上的点来表示出来(1)如下图,以单位长度为边长画一个正方形,以原点为圆心,正方形对角线为半径画弧,与正、负半轴的交点分别为点A和点B,数轴上A点和B点对应的数是什么?
(2)如果将所有有理数都标到数轴上,那么数轴 填满吗?BA每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一点都表示一个实数。即实数和数轴上的点是一一对应的。C在数轴上表示的两个实数,右边的数总比左边的数___。数轴上的点有些
表示有理数,有
些表示无理数.大在数轴上表示的两个实数,右边的数总
比左边的数大。
例:把下列实数表示在数轴上,并比较它们的大小(用“<”号连接) 例:把下列实数表示在数轴上,并比较它们的大小(用“<”号连接)想一想1、无理数与无理数的和、差、积、
商仍是无理数吗?
2、无理数都是无限小数吗?
3、无限小数都是无理数吗?
4、带根号的数都是无理数吗? 作业:P178--2、3
布置作业 谢 谢 !
(1)若正方形的边长是6,则它的面积是 (2)若正方形的边长是a,则它的面积是 (3)若正方形的面积是25,则它的边长是(4)若正方形的面积是2,则它的边长是 365把两个边长为1的小正方形通过剪、拼,设法得到一个大正方形剪一剪 拼一拼11则此时大正方形的边长为多少? 是不是有理数? 把下列各有理数数写成小数的形式,你有什么 发现?探究有理数的特征 事实上,任何一个有理数都可以写成有限小数或 无限且循环小数。1.414 213 562 373 095 048 801 688 724 209 6……我们把这种_____________叫做无理数。是不是整数?是不是分数?由计算机可得无限不循环小数不是不是≈
例如:圆周率 及一些含有 的数是否无理数?是 理由:______无限不循环小数
像 的数是否为无理数?
是
理由:______无限不循环小数哪?有一定的规律,但不循环的无限小数都是无理数。0.1010010001…
—234.232232223…
0.12345678910111213 …〔两个3之间依次多1个2〕〔小数部分有相继的正整数组成〕〔两个1之间依次多1个0〕观察A 有理数B无理数练习、判断下列数哪些是有理数?哪些是无理数? 有理数是:
无理数是:
, , , ,有理数和无理数统称为实数。(无限不循环小数)(有限小数和无限循环小数)由于不是0的有理数和无理数都有正负之分
则实数也可以这样分类
把数从有理数扩充到实数以后,有理数的相反数和绝对值的概念同样适用于实数。因为
所以绝对值等于 的数是 和
例如:已知一个数的绝对值是 ,求这个数
解:
(1) 的相反数是__________
(2) 的相反数是
(3) ___________
(4)绝对值等于 的数是 _________ 试一试结论实数a的相反数是______
一个正数的绝对值是它______
一个负数的绝对值是它的_______
0的绝对值还是_________-a本身相反数0OO′的长是这个圆的周长 ,所以点O′的坐标是问题:每个有理数都可以用数轴上的点来表示.
无理数是否也可以用数轴上的点来表示出来呢?无理数 可以用数轴上的点来表示出来(1)如下图,以单位长度为边长画一个正方形,以原点为圆心,正方形对角线为半径画弧,与正、负半轴的交点分别为点A和点B,数轴上A点和B点对应的数是什么?
(2)如果将所有有理数都标到数轴上,那么数轴 填满吗?BA每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一点都表示一个实数。即实数和数轴上的点是一一对应的。C在数轴上表示的两个实数,右边的数总比左边的数___。数轴上的点有些
表示有理数,有
些表示无理数.大在数轴上表示的两个实数,右边的数总
比左边的数大。
例:把下列实数表示在数轴上,并比较它们的大小(用“<”号连接) 例:把下列实数表示在数轴上,并比较它们的大小(用“<”号连接)想一想1、无理数与无理数的和、差、积、
商仍是无理数吗?
2、无理数都是无限小数吗?
3、无限小数都是无理数吗?
4、带根号的数都是无理数吗? 作业:P178--2、3
布置作业 谢 谢 !
