实数第二课时[下学期]

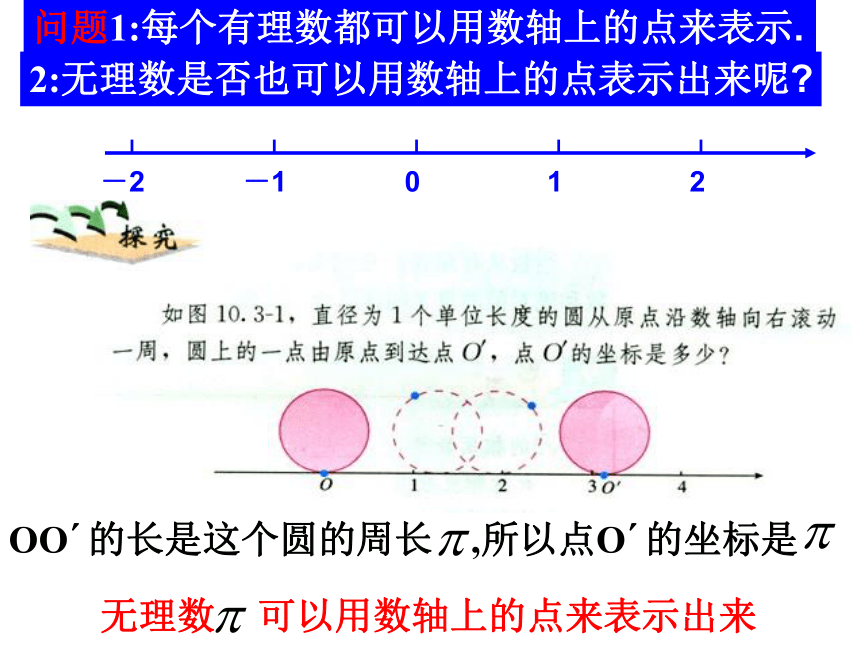
课件31张PPT。10.3实数(2)温岭四中初一数学组 有理数集合 无理数集合1.把下列各数分别填入相应的集合中：P1780.121121112…..0.121121112…..OO′的长是这个圆的周长 ,所以点O′的坐标是问题1:每个有理数都可以用数轴上的点来表示.
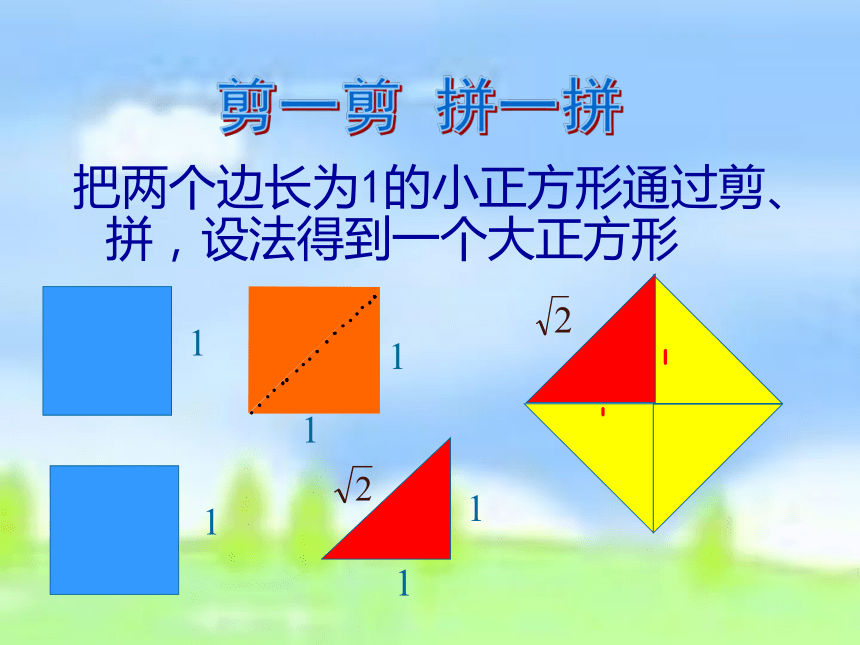
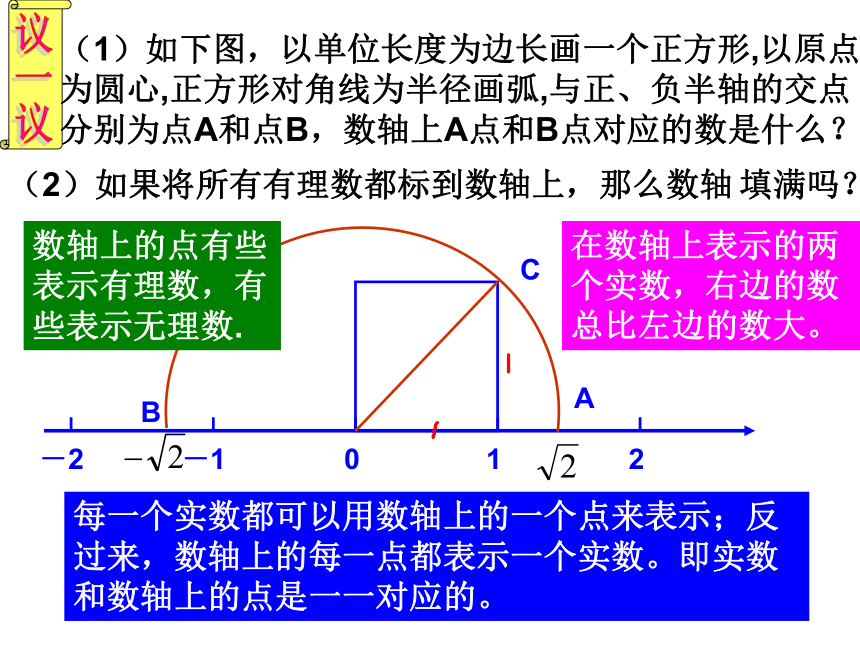
无理数 可以用数轴上的点来表示出来2:无理数是否也可以用数轴上的点表示出来呢?把两个边长为1的小正方形通过剪、拼，设法得到一个大正方形剪一剪 拼一拼11（1）如下图，以单位长度为边长画一个正方形,以原点为圆心,正方形对角线为半径画弧,与正、负半轴的交点分别为点A和点B，数轴上A点和B点对应的数是什么？
（2）如果将所有有理数都标到数轴上，那么数轴 填满吗？BA每一个实数都可以用数轴上的一个点来表示；反过来，数轴上的每一点都表示一个实数。即实数和数轴上的点是一一对应的。C在数轴上表示的两个实数，右边的数总比左边的数大。数轴上的点有些
表示有理数，有
些表示无理数.随堂练习：P178解:点A表示-1.5; 点B表示 ;点C表示 ;点D表示3;点E表示 . 判断下列说法是否正确：2 所有的实数都可以用数轴上的点表示,反过来,数轴上所有的点都表示实数。（ ）×P1781.所有的有理数都可以用数轴上的点表示,反过来,数轴上所有的点都表示有理数。（ ）判断下列实数的运算是否正确：乘法交换律乘法结合律分配律 实数和有理数一样也可以进行加、减、乘、除(除数不为0)、乘方运算，而且正数及0可以进行开平方运算,任意一个实数可以进行开立方运算.在进行实数的运算时,有理数的运算律和运算法则在实数范围内同样适用随着数的进一步扩充,在比实数更大的数集---复数中,负数将可以进行开平方运算. 有理数的运算法则与运算律对实数仍然适用。例1、计算下列各式的值:(2)｜ ｜解:(分配律)(加法结合律)练习3.计算解:(2)｜ ｜P178例2、计算:≈3.46+3.14≈6.60≈1.732×1.414≈2.45解:≈3.464+3.142≈6.61×取近似数时要注意中间过程取的位数要比结果保留的位数要_______多一位做一做：
1、2、利用计算器计算：你发现了什么规律？2×3=66.486.48做一做
3、4、利用计算器计算：你又发现了什么规律？0.9260.926通过这节课的学习,你有哪些收获？≈ ×2.24×1.41≈1.6答:?OAB的面积约是1.6.S?OAB=解:由已知可得OB= ,?OAB的OB边上的高为 变题:如图,点B的坐标为( ,0), ?OAB
面积为 ,点A的坐标为(1, y )
求A点的纵坐标.?OAB的OB边上的高为|y|.
∵S?OAB=∴ × × | y | =∴| y |=∴y =±∵点A在第一象限∴A点的纵坐标是解: (1)围成的四边形ABCD是长方形.(2)由已知AB=5-2=3,AD=(3)A、B、C、D四点的坐标分别变为(2, )、(5, )、
( 5, 0)、( 2, 0)P179四边形ABCD的面积=AB×AD =P184D则四边形OABC的面积=OC×BD =:(3)过点B作BD⊥x轴于点D.解∵四边形ABCO是平形四边形,∴AB平行CO,AB=CO∵ AB平行CO,∴B点的___坐标与A点___坐标相同,为_____∵AB=CO,∴B点的_____坐标到A的距离为______∴B点的__坐标为_______纵纵横横P184解：将h=1.5代入公式s2=16.88h,得s2=25.32,≈5.03(km)将h=35代入公式s2=16.88h,得s2=590.8,≈24.31.03(km)P179解:将l=0.5m代入公式t=2 ,得t≈2×3.14×0.22t≈1.4 （s）答:小重物来回摆动一次所用的时间约1.4s。解: 设圆的半径为r cm,正方形的边长为a cm.由题意,得 r2=2 , a2=2 ∴圆的周长C1=2 r =2 ∴C1（1） 的相反数是__________ （5） 绝对值是 _________ （2） 的倒数是____,（3）｜ ｜=___________（4）绝对值等于 的数是 _________ 的平方 是___ 　．正实数的绝对值是　　　　；
０的绝对值是　　　　　　；
负实数的绝对值是　　 。它本身0它的相反数４、　　　　的绝对值是 。４