13.3.1等腰三角形(2) 课件(共23张PPT)
文档属性
| 名称 | 13.3.1等腰三角形(2) 课件(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-16 20:20:09 | ||
图片预览




文档简介
(共23张PPT)
人教版 八年级上册
13. 3.1 等腰三角形(2)
教学目标
1.经历等腰三角形的判定定理的发现过程。
2.掌握等腰三角形的判定定理:在同一个三角形中,等角对等边。
3.会用等腰三角形的判定进行简单的推理、判断、计算和作图。
教学重点:等腰三角形的判定方法及其运用。
教学难点:等腰三角形判定方法证明中添加辅助线的思想方法以及等腰三角形性质与判定的区别. 等腰三角形性质与判定同时运用说理过程的思路难以形成
1.等腰三角形的性质定理是什么?
等腰三角形的两个底角相等.
2.这个定理的逆命题是什么?
如果一个三角形有两个角相等,
3.猜想这个命题正确吗?
那么这个三角形是等腰三角形.
(可以简称:等边对等角)
复习旧知
已知:△ABC中,∠B=∠C.
求证:AB=AC
证明:
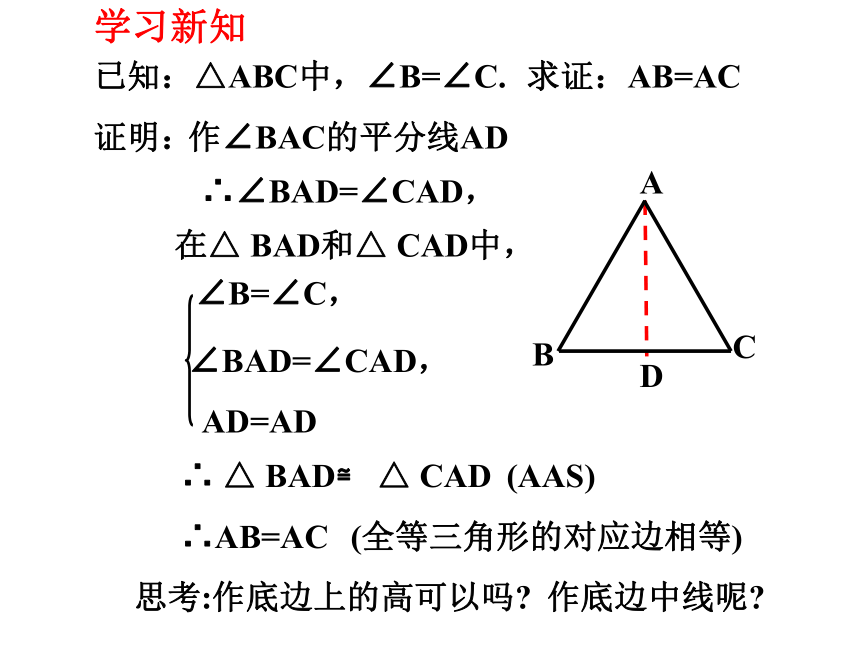
作∠BAC的平分线AD
在△ BAD和△ CAD中,
∠B=∠C,
∴ △ BAD≌ △ CAD
∴AB=AC
A
B
C
D
思考:作底边上的高可以吗
AD=AD
∠BAD=∠CAD,
∴∠BAD=∠CAD,
作底边中线呢
(AAS)
(全等三角形的对应边相等)
学习新知
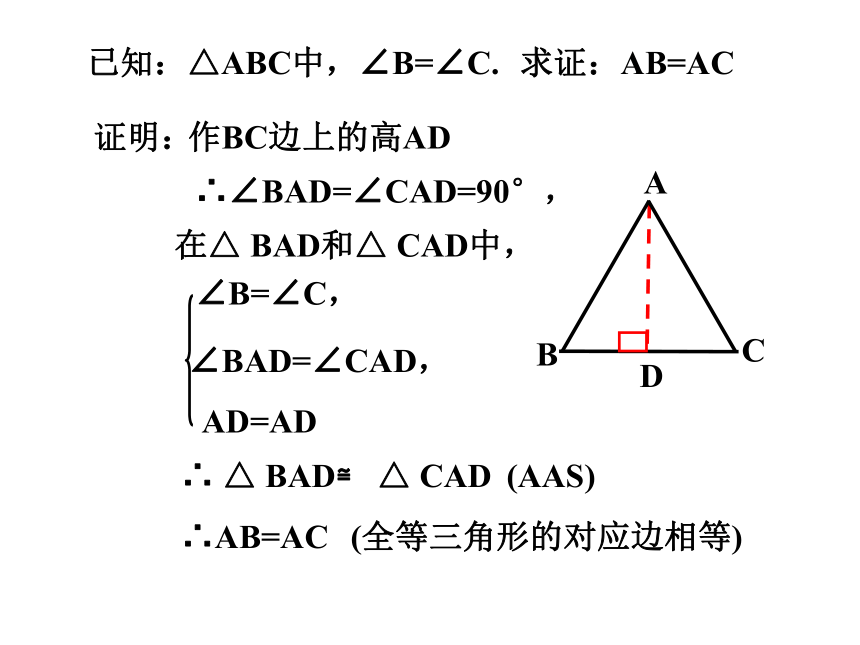
已知:△ABC中,∠B=∠C.
求证:AB=AC
证明:
作BC边上的高AD
在△ BAD和△ CAD中,
∠B=∠C,
∴ △ BAD≌ △ CAD
∴AB=AC
A
B
C
D
AD=AD
∠BAD=∠CAD,
∴∠BAD=∠CAD=90°,
(AAS)
(全等三角形的对应边相等)
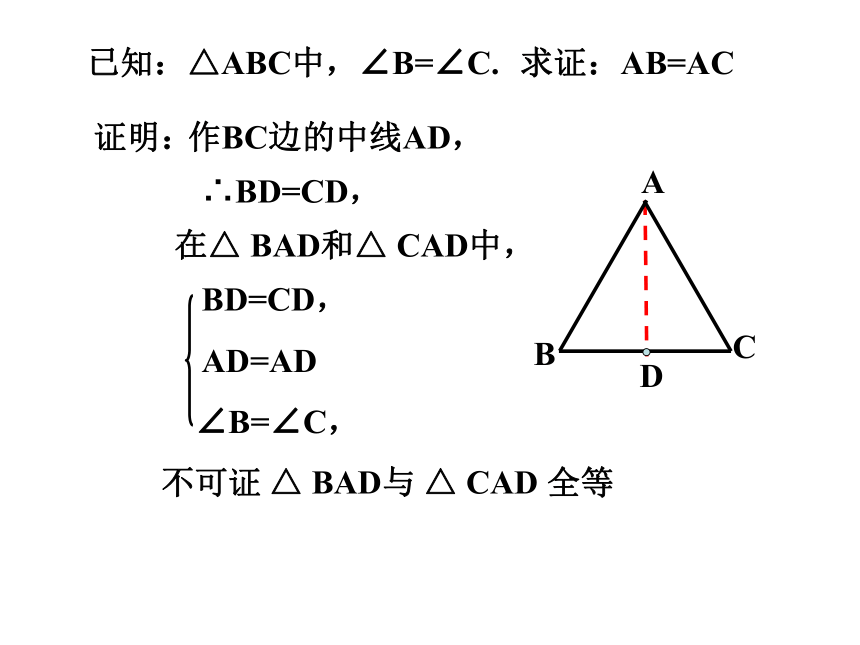
已知:△ABC中,∠B=∠C.
求证:AB=AC
证明:
作BC边的中线AD,
在△ BAD和△ CAD中,
∠B=∠C,
A
B
C
D
AD=AD
BD=CD,
∴BD=CD,
不可证
△ BAD与 △ CAD
全等
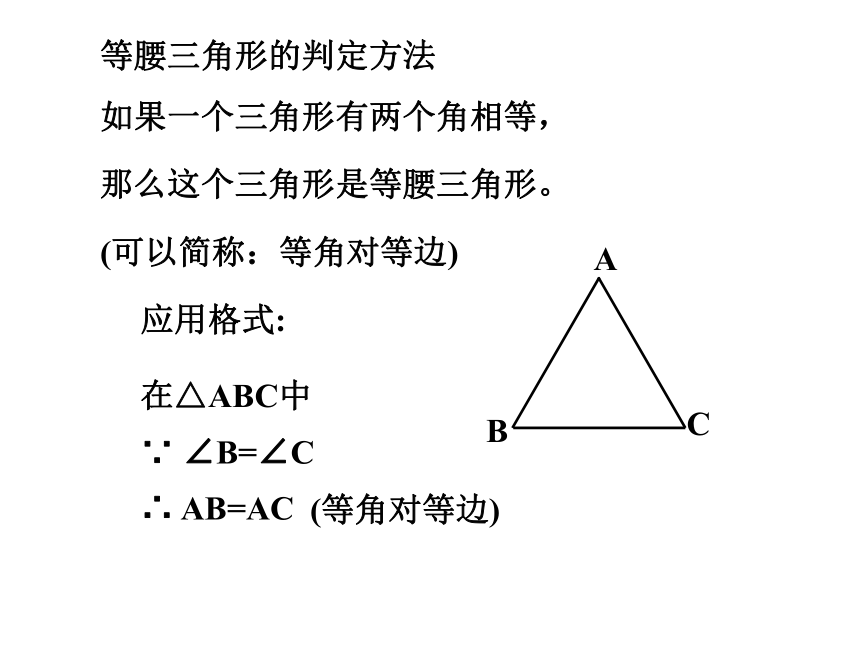
等腰三角形的判定方法
A
B
C
应用格式:
在△ABC中
∵ ∠B=∠C
∴ AB=AC
如果一个三角形有两个角相等,
那么这个三角形是等腰三角形。
(可以简称:等角对等边)
(等角对等边)
例1 :求证:如果三角形一个外角的平分线平行于
三角形的一边,那么这个三角形是等腰三角形.
A
B
C
D
E
1
2
如图,∠CAE是△ABC的外角,∠1=∠2,
求证:AB=AC
已知:
要证 : AB=AC,
分析:
AD∥BC
要证 :∠B=∠C,
要证 :∠B=∠1,
∠C=∠2,
AD∥BC.
例题解析
A
B
C
D
E
1
2
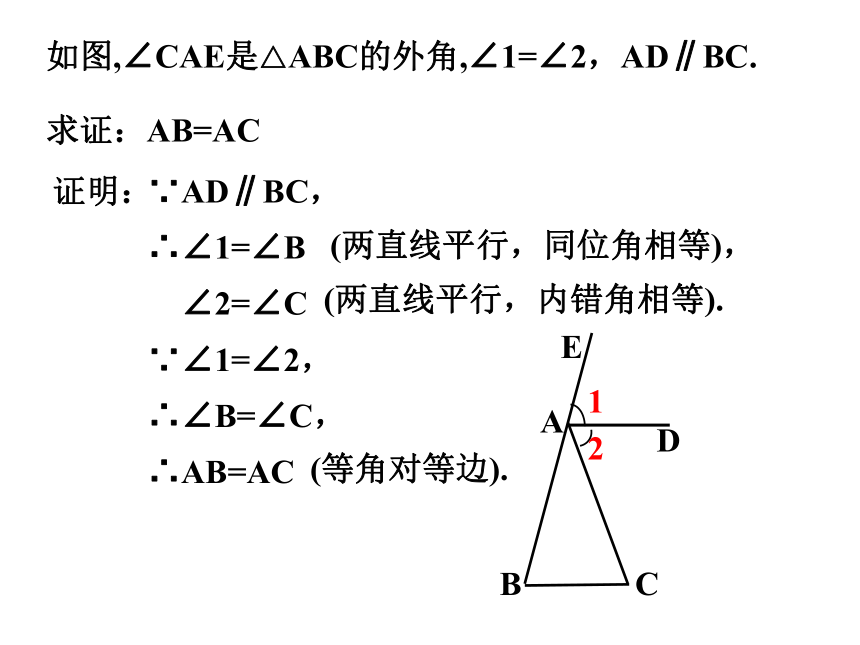
如图,∠CAE是△ABC的外角,∠1=∠2,AD∥BC.
求证:AB=AC
证明:
∵AD∥BC,
∴∠1=∠B
∠2=∠C
∵∠1=∠2,
∴∠B=∠C,
∴AB=AC
(两直线平行,内错角相等).
(等角对等边).
(两直线平行,同位角相等),
C
B
A
D
1
2
1.已知:如图∠A=36°,∠DBC =36°, ∠C=72°。计算∠1和∠2,并说明图中有哪些等腰三角形?
等腰三角形有:
∠A+∠2
解:
∵∠DBC=36°,
C=72°,
∴∠1=180°-∠DBC
-∠C
=180°-36°
- 72°,
=72°
∵∠1=
∴∠2= -∠A
∠1
=72°-36°
=36°,
△ ABD,
△ BCD。
△ ABC,
练习巩固
2.如图,把一张长方形的纸沿对角线折叠,重合部分 是一个等腰三角形吗?为什么?
A
D
C
B
答:重合部分是一个等腰三角形。
E
∵△ BCD和△ BED关于BD对称,
∴ △ BCD≌ △ BED,
∴∠EBD=∠CBD.
∵AD∥BC,
∴∠ADB=∠CBD,
∴∠ABD=∠ADC,
∴AB=AD.
3.求证:如果三角形一条边上的中线等于这条边的一半,
那么这个三角形是直角三角形。
如图, △ABC 中,CD是AB边上的中线,且CD = AB.
求证:
△ABC 是直角三角形.
B
A
D
C
1
2
证明:
∵CD是AB边上的中线,
∴AD= AB,
BD= AB,
∵CD= AB,
∴AD=CD,
BD=CD,
∴∠A=∠ACD,
∠B=∠BCD,
∵∠A+∠B
+∠ACD+∠BCD
=180°,
∴∠A+∠B
= 90°,
∴△ABC 是直角三角形.
1
2
1
2
1
2
4.如图,AC和BD相交于点O,AB∥DC,OA=OB.
求证:OC=OD.
B
A
D
C
O
证明:
∵AB∥DC,
∴∠A=∠C,
∠B =∠D.
∵OA = OB,
∴∠A=∠B
∴OC = OD
∴∠C=∠D,
(等角对等边).
(等边对角等).
B
A
D
C
已知:如图,AD ∥BC,BD平分∠ABC.
求证:AB=AD.
∵ AD ∥BC ,
∴∠ADB=∠DBC.
∵BD 平分∠ ABC,
∴∠ABD=∠DBC.
∴∠ABD=∠ADB,
∴AB=AD
证明:
(等角对等边).
例.已知:如图,CD为Rt△ABC斜边AB上的高, ∠BAC的平分线交CD,CB于点E,F,FG⊥AB,垂足为点G.
求证:CE=FG.
A
B
D
C
E
F
G
1
2
要证: ∠1=∠2.
要证: CE=FG.
要证: ∠3=∠4.
要证: CE= CF.
AF平分∠BAC
3
4
5
例题解析
已知:如图,CD为Rt△ABC斜边AB上的高, ∠BAC的平分线交CD,CB于点E,F,FG⊥AB,垂足为点G.
求证:CE=FG.
A
B
D
C
E
F
G
1
2
3
4
5
证明:
∵AF平分∠BAC,
∴∠3=∠4.
∵FC⊥AC,
FG⊥AB,
∴FC=FG.
∵CD⊥AB,
∴∠CDA=90°,
∴∠4+∠5=90°.
∵∠BCA=90°,
∴∠3+∠2=90°.
∴∠2=∠5.
∵∠1=∠5.
∴∠1=∠2.
∴FC=CE.
∴CE=FG.
1. 已知等腰三角形的一个内角为70°,则另两个角的度数是( ).
A.55°,55° B.70°,40°
C.55°,55°或70°,40° D.以上都不对
2. 已知等腰三角形的一个内角为100°,则另两个角的度数是( ).
A.100°,40° B.40°,40°
C.100°,40°或40°,40° D.以上都不对
C
B
巩固提高
3.△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连结DE,则△CDE的周长为( )
A.20 B.12 C.14 D.13
A
B
C
E
D
C
4.已知:如图, AB与CD交于点P,CP=PD,∠A=42°, ∠CPB=138°,∠B=69°,求证:AC=PB.
∵ ∠CPB+∠APC =180°,
∴∠APC =180°-∠CPB
=180°-138°
=42°.
∵ ∠A =42°,
∴∠A=∠APC,
∴CA=CP,
∵ ∠CPB=∠B+∠D ,
∴∠ D=∠CPB-∠B
=138°-69°
=69°.
∴∠ D=∠B,
∴PB=PD.
∴CP=PD,
∴CA=PB.
解:
B
A
D
C
P
5.如图,在△ABC中,AB =AC, DE∥BC,点F是BC 的中点,连接FD,FE. 求证:FD=FE.
A
B
C
D
E
F
证明:
∵ AB=AC ,
∴∠ B=∠C,
∵DE∥BC,
∴∠ADE=∠B,
∠AED=∠C,
∴∠ADE=∠AED,
∴AE=AE,
∴DB=EC,
∵点F是BC 的中点,
∴BF=CF,
∴ △BDF≌△CEF
(SAS).
∴FD=FE.
今天作业
课本P82页第4、5题
课本P83页第10题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 八年级上册
13. 3.1 等腰三角形(2)
教学目标
1.经历等腰三角形的判定定理的发现过程。
2.掌握等腰三角形的判定定理:在同一个三角形中,等角对等边。
3.会用等腰三角形的判定进行简单的推理、判断、计算和作图。
教学重点:等腰三角形的判定方法及其运用。
教学难点:等腰三角形判定方法证明中添加辅助线的思想方法以及等腰三角形性质与判定的区别. 等腰三角形性质与判定同时运用说理过程的思路难以形成
1.等腰三角形的性质定理是什么?
等腰三角形的两个底角相等.
2.这个定理的逆命题是什么?
如果一个三角形有两个角相等,
3.猜想这个命题正确吗?
那么这个三角形是等腰三角形.
(可以简称:等边对等角)
复习旧知
已知:△ABC中,∠B=∠C.
求证:AB=AC
证明:
作∠BAC的平分线AD
在△ BAD和△ CAD中,
∠B=∠C,
∴ △ BAD≌ △ CAD
∴AB=AC
A
B
C
D
思考:作底边上的高可以吗
AD=AD
∠BAD=∠CAD,
∴∠BAD=∠CAD,
作底边中线呢
(AAS)
(全等三角形的对应边相等)
学习新知
已知:△ABC中,∠B=∠C.
求证:AB=AC
证明:
作BC边上的高AD
在△ BAD和△ CAD中,
∠B=∠C,
∴ △ BAD≌ △ CAD
∴AB=AC
A
B
C
D
AD=AD
∠BAD=∠CAD,
∴∠BAD=∠CAD=90°,
(AAS)
(全等三角形的对应边相等)
已知:△ABC中,∠B=∠C.
求证:AB=AC
证明:
作BC边的中线AD,
在△ BAD和△ CAD中,
∠B=∠C,
A
B
C
D
AD=AD
BD=CD,
∴BD=CD,
不可证
△ BAD与 △ CAD
全等
等腰三角形的判定方法
A
B
C
应用格式:
在△ABC中
∵ ∠B=∠C
∴ AB=AC
如果一个三角形有两个角相等,
那么这个三角形是等腰三角形。
(可以简称:等角对等边)
(等角对等边)
例1 :求证:如果三角形一个外角的平分线平行于
三角形的一边,那么这个三角形是等腰三角形.
A
B
C
D
E
1
2
如图,∠CAE是△ABC的外角,∠1=∠2,
求证:AB=AC
已知:
要证 : AB=AC,
分析:
AD∥BC
要证 :∠B=∠C,
要证 :∠B=∠1,
∠C=∠2,
AD∥BC.
例题解析
A
B
C
D
E
1
2
如图,∠CAE是△ABC的外角,∠1=∠2,AD∥BC.
求证:AB=AC
证明:
∵AD∥BC,
∴∠1=∠B
∠2=∠C
∵∠1=∠2,
∴∠B=∠C,
∴AB=AC
(两直线平行,内错角相等).
(等角对等边).
(两直线平行,同位角相等),
C
B
A
D
1
2
1.已知:如图∠A=36°,∠DBC =36°, ∠C=72°。计算∠1和∠2,并说明图中有哪些等腰三角形?
等腰三角形有:
∠A+∠2
解:
∵∠DBC=36°,
C=72°,
∴∠1=180°-∠DBC
-∠C
=180°-36°
- 72°,
=72°
∵∠1=
∴∠2= -∠A
∠1
=72°-36°
=36°,
△ ABD,
△ BCD。
△ ABC,
练习巩固
2.如图,把一张长方形的纸沿对角线折叠,重合部分 是一个等腰三角形吗?为什么?
A
D
C
B
答:重合部分是一个等腰三角形。
E
∵△ BCD和△ BED关于BD对称,
∴ △ BCD≌ △ BED,
∴∠EBD=∠CBD.
∵AD∥BC,
∴∠ADB=∠CBD,
∴∠ABD=∠ADC,
∴AB=AD.
3.求证:如果三角形一条边上的中线等于这条边的一半,
那么这个三角形是直角三角形。
如图, △ABC 中,CD是AB边上的中线,且CD = AB.
求证:
△ABC 是直角三角形.
B
A
D
C
1
2
证明:
∵CD是AB边上的中线,
∴AD= AB,
BD= AB,
∵CD= AB,
∴AD=CD,
BD=CD,
∴∠A=∠ACD,
∠B=∠BCD,
∵∠A+∠B
+∠ACD+∠BCD
=180°,
∴∠A+∠B
= 90°,
∴△ABC 是直角三角形.
1
2
1
2
1
2
4.如图,AC和BD相交于点O,AB∥DC,OA=OB.
求证:OC=OD.
B
A
D
C
O
证明:
∵AB∥DC,
∴∠A=∠C,
∠B =∠D.
∵OA = OB,
∴∠A=∠B
∴OC = OD
∴∠C=∠D,
(等角对等边).
(等边对角等).
B
A
D
C
已知:如图,AD ∥BC,BD平分∠ABC.
求证:AB=AD.
∵ AD ∥BC ,
∴∠ADB=∠DBC.
∵BD 平分∠ ABC,
∴∠ABD=∠DBC.
∴∠ABD=∠ADB,
∴AB=AD
证明:
(等角对等边).
例.已知:如图,CD为Rt△ABC斜边AB上的高, ∠BAC的平分线交CD,CB于点E,F,FG⊥AB,垂足为点G.
求证:CE=FG.
A
B
D
C
E
F
G
1
2
要证: ∠1=∠2.
要证: CE=FG.
要证: ∠3=∠4.
要证: CE= CF.
AF平分∠BAC
3
4
5
例题解析
已知:如图,CD为Rt△ABC斜边AB上的高, ∠BAC的平分线交CD,CB于点E,F,FG⊥AB,垂足为点G.
求证:CE=FG.
A
B
D
C
E
F
G
1
2
3
4
5
证明:
∵AF平分∠BAC,
∴∠3=∠4.
∵FC⊥AC,
FG⊥AB,
∴FC=FG.
∵CD⊥AB,
∴∠CDA=90°,
∴∠4+∠5=90°.
∵∠BCA=90°,
∴∠3+∠2=90°.
∴∠2=∠5.
∵∠1=∠5.
∴∠1=∠2.
∴FC=CE.
∴CE=FG.
1. 已知等腰三角形的一个内角为70°,则另两个角的度数是( ).
A.55°,55° B.70°,40°
C.55°,55°或70°,40° D.以上都不对
2. 已知等腰三角形的一个内角为100°,则另两个角的度数是( ).
A.100°,40° B.40°,40°
C.100°,40°或40°,40° D.以上都不对
C
B
巩固提高
3.△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连结DE,则△CDE的周长为( )
A.20 B.12 C.14 D.13
A
B
C
E
D
C
4.已知:如图, AB与CD交于点P,CP=PD,∠A=42°, ∠CPB=138°,∠B=69°,求证:AC=PB.
∵ ∠CPB+∠APC =180°,
∴∠APC =180°-∠CPB
=180°-138°
=42°.
∵ ∠A =42°,
∴∠A=∠APC,
∴CA=CP,
∵ ∠CPB=∠B+∠D ,
∴∠ D=∠CPB-∠B
=138°-69°
=69°.
∴∠ D=∠B,
∴PB=PD.
∴CP=PD,
∴CA=PB.
解:
B
A
D
C
P
5.如图,在△ABC中,AB =AC, DE∥BC,点F是BC 的中点,连接FD,FE. 求证:FD=FE.
A
B
C
D
E
F
证明:
∵ AB=AC ,
∴∠ B=∠C,
∵DE∥BC,
∴∠ADE=∠B,
∠AED=∠C,
∴∠ADE=∠AED,
∴AE=AE,
∴DB=EC,
∵点F是BC 的中点,
∴BF=CF,
∴ △BDF≌△CEF
(SAS).
∴FD=FE.
今天作业
课本P82页第4、5题
课本P83页第10题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
